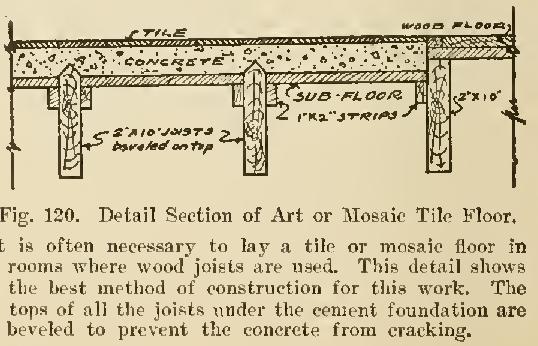
Tile Work

TILE WORK The vigorous sanitary campaigns now being carried on by the Health Boards of several great States—notably Ohio and Michigan—and by a number of the Health Commissions of leading cities, such as Chicago, New York, and Pittsburgh, has concentrated the home-builder's attention on materials which will assist in keeping the home in a sanitary condition. Mosaic tiles for lobbies and bathrooms, and tile wainscoting for vestibules, kitch ens, and bathrooms, are now being considered indispensable in up-to-d'ate sanitary construction.

When tile work is to be estimated, Table XXIX will prove of value to the contractor. This table gives not only the shape and size of many of the common tiles, but also gives the number of each kind which is required to fill exactly one square foot of space. An allowance of a small number shall be made for breakage and losses.

For example, if we have a section of tile wainscoting 8 feet long and 5 feet high, coin. posed of oblong white tiles 6 x I inches in size, and a border along the top made from blue and white triangle or diagonal tile 6 x 6 inches in size, to find the number of tiles needed for this piece of work, we proceed as follows: The area to be covered by the oblong tiles is 8 ft. long and 4y. ft. high.

8 X 4% = 30 square feet.

There are 144 square inches ht one square foot; therefore, 36 X 144 = 5,184 square inches.

Now, mince 1 .oblong tile, size 6 tt 1% inches, eon. tains: 6 X 1%3=9 square ladies, the reset number of tiles needed for the part 8 ft. long below the border, is: 5,184 tiles.

9 Better make this 600, to allow for loss and break. age.

Now that we have seen the principle involved in this calculation, we shall explain the method of using Table XXIX, and see if the results cheek in value. From our figures above, we have 36 square feet below the border. This space is to be filled with 6 x 11/2-inch tiles. From the table, the number of 6 x 11/2 inch oblong tiles which are necessary to cover one square foot of surface is 16. Therefore, 36X16=576 tiles required.

This result checks with our first figures.

For the border of diagonal tiles, we have an area 8 feet long by foot high which is to be filled.

X 1/2= 4 square feet.

From the table (second line from top), we find that we shall need 8 diagonal GxG-inch tiles per square foot. Therefore, 4X8= 32 tiles required for border.

Better make this 40, to allow again for loss and breakage. This would mean 20 blue and 20 white diagonal tiles.

This same principle may be used in figurhig ether sizes of walls, and in using other sizes of tiles.