Muslim - Chronology
MUSLIM - CHRONOLOGY The Muslim Calendar (see CALENDAR : Muslim) may evidently be carried on indefinitely by successive addition, provided care be taken to allow for the additional day occurring in bissextile and intercalary years. The purely lunar years of this calendar are partitioned into cycles of 3o years, 19 of which are common years of 354 days each, the remaining I 1 being intercalary years having an additional day appended to the last month. The mean length of the year is, therefore, 354e- days (354 days, 8 hours, 48 minutes). This gives 29 days (29 days, 12 hours, 44 minutes) as a period of mean lunation, and this differs from the astronomical mean lunation by only 2.8 seconds. This small error amounts to a day in about 2,400 years.
To find if a year is intercalary or common, divide it by 3o ; the quotient will be the number of completed cycles and the re mainder will be the year of the current cycle ; if this last be one of the numbers 2, 5, 7, Io, 13, 16, 18, 21, 24, 26, 29, the year is intercalary and consists of 355 days; if it be any other number, the year is ordinary.
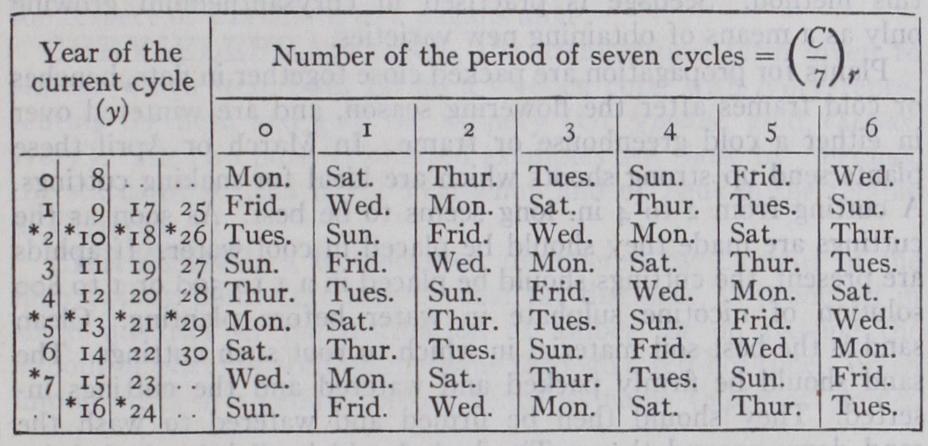
To find from this table the day of the week on which any year of the Hejira begins, the rule to be observed will be as follows : Rule.—Divide the year of the Hejira by 3o; the-quotient is the number of cycles, and the remainder is the year of the current cycle. Next divide the number of cycles by 7, and the second remainder will be the Number of the Period, which being found at the top of the table, and the year of the cycle on the left hand, the required day of the week is immediately shown.
The intercalary years of the cycle are distinguished by an asterisk.
For the computation of the Christian date, the ratio of a mean year of the Hejira to a solar year is : The year I began July 16, 622, Old Style, or July 19, 622, accord ing to the New or Gregorian Style. Now the day of the year an swering to July 19, is 200, which, in parts of the solar year, is 76, and the number of years elapsed= Y —1. Therefore, as the intercalary days are distributed with considerable regularity in both calendars, the date of commencement of the year Y ex pressed in Gregorian years is: This formula gives the following rule for calculating the date of the commencement of any year of the Hejira, according to the Gregorian or New Style.
Rule.—Multiply 970,224 by the year of the Hejira, cut off six decimals from the product, and add The sum will be the year of the Christian era, and the day of the year will be found by multiplying the decimal figures by 365.
The result may sometimes differ a day from the truth, as the intercalary days do not occur simultaneously; but as the day of the week can always be accurately obtained from the foregoing table, the result can be readily adjusted.
