Scalenohedral Class
SCALENOHEDRAL CLASS (Bisphenoidal-hemihedral.) Here there are only three dyad axes and two planes of sym metry, the former coinciding with the crystallographic axes and the latter bisecting the angles between the horizontal pair. The dyad axis of symmetry, which in this class coincides with the principal axis of the crystal, has certain of the characters of a tetrad axis, and is sometimes called a tetrad axis of "alternating symmetry" ; a face on the upper half of the crystal if rotated through 90° about this axis and reflected across the equatorial plane falls into the position of a face on the lower half of the crystal. This kind of symmetry, with simultaneous rotation about an axis and reflection across a plane, is also called "composite symmetry." In this class all except two of the simple forms are geometrically the same as in the holosymmetric class.
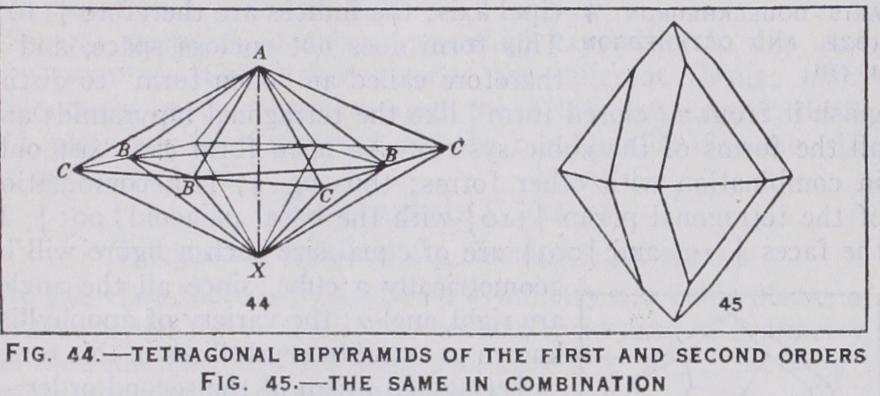
Bisphenoid a wedge) (fig. 5o).— This is a double wedge-shaped solid bounded by four equal isosceles triangles; it has the indices {III } , { 21 1 } , { 1121, etc., or in general { hhl } . By suppressing either one or other set of alternate faces of the tetragonal bipyramid of the first order (fig. 4 2) two bisphenoids are derived in the same way that two tetrahedra are derived from the regular octahedron.
Tetragonal scalenohedron or ditetrag onal bisphenoid (fig. 50.—This is bounded by eight scalene triangles and has the indices { hkl } . It may be considered as the hemihedral form of the ditetragonal bipyramid.
The crystal of chalcopyrite represented in fig. 52 is a combination of two bisphenoids (P and P'), two bipyramids of the second order (b and c), and the basal pinacoid (a). Stannite acid potassium phosphate ), mercuric cya nide, and urea also crystallize in this class.