CONDUCTION OF, IN GASES A gas such as air when it is under normal conditions conducts electricity to a small but only to a very small extent, however small the electric force acting on the gas may be. The electrical conductivity of gases not exposed to special conditions is so small that it was only definitely established in the early years of the loth century, although it had engaged the attention of physicists for more than a hundred years. It had been known for a long time that a body charged with electricity slowly lost its charge even when insulated with the greatest care, and though long ago some physicists believed that part of the leak of electricity took place through the air, the general view seems to have been that it was due to almost unavoidable defects in the insulation or to dust in the air, which after striking the charged body was repelled from it and went off with some of the charge. C. A. Coulomb, who made some very careful experiments which were published in 1785 (Mem. de l'Acad. des Sciences, 1785, p. 612), came to the conclusion that after allowing for the leakage along the threads which supported the charged body there was a balance over, which he attributed to leakage through the air. His view was that when the molecules of air come into contact with a charged body some of the electricity goes on to the mole cules, which are then repelled from the body carrying their charge with them. We shall see later that this explanation is not tenable. C. Matteucci (Ann. claim. phys., 185o, 28, p. 39o) in 185o also came to the conclusion that the electricity from a charged body passes through the air ; he was the first to prove that the rate at which electricity escapes is less when the pressure of the gas is low than when it is high. He found that the rate was the same whether the charged body was surrounded by air, carbonic acid or hydrogen. Subsequent investigations have shown that the rate in hydrogen is in general much less than in air. Thus in 1872 E. G. Warburg (Pogg. Ann,, 1872, P. found that the leak through hydrogen was only about one-half of that through air : he confirmed Matteucci's observations on the effect of pressure on the rate of leak, and also found that it was the same whether the gas was dry or damp. He was inclined to attribute the leak to dust in the air, a view which was strengthened by an experiment of J. W. Hittorf's (Wied. Ann., 7, p. 595), in which a small carefully insulated electroscope, placed in a small vessel filled with carefully filtered gas, retained its charge for several days ; we know now that this was due to the smallness of the vessel and not to the absence of dust, as it has been proved that the rate of leak in small vessels is less than in large ones.
Great light was thrown on this subject by some experiments on the rates of leak from charged bodies in closed vessels made almost simultaneously by H. Geitel (Plays. Zeit., 1900, 2, p. I16) and C. T. R. Wilson (Proc. Camb. Phil. Soc., 1900, I I, p. 32). These observers established that (I) the rate of escape of electricity in a closed vessel is much smaller than in the open, and the larger the vessel the greater is the rate of leak; and (2) the rate of leak does not increase in proportion to the differences of potential between the charged body and the walls of the vessel: the rate soon reaches a limit beyond which it does not increase, however much the potential difference may be increased, provided, of course, that this is not great enough to cause sparks to pass from the charged body. On the assumption that the maximum leak is proportional to the volume, Wilson's experiments, which were made in vessels less than 1 litre in volume, showed that in dust-free air at atmospheric pressure the maximum quantity of electricity which can escape in one second from a charged body in a closed volume of V cubic centimetres is about electrostatic units.
E. Rutherford and S. T. Allan (Phys. Zeit., 1902, 3, p. 225), working in Montreal, obtained results in close agreement with this. Working between pressures of from 43 to 743 millimetres of mercury, Wilson showed that the maximum rate of leak is very approximately proportional to the pressure ; it is thus exceedingly small when the pressure is low-a result illustrated in a striking way by an experiment of Sir W. Crookes (Proc. Roy. Soc., 1879, 28, p. 347) in which a pair of gold leaves retained an electric charge for several months in a very high vacuum. Subsequent experiments have shown that it is only in very small vessels that the rate of leak is proportional to the volume and to the pressure; in large vessels the rate of leak per unit volume is considerably smaller than in small ones. In small vessels the maximum rate of leak in different gases, is, with the exception of hydrogen, approximately proportional to the density of the gas. Wilson's results on this point are shown in the following table (Proc. Roy. Soc., 190I, 6o, p. The rate of leak of electricity through gas contained in a closed vessel depends to some extent on the material of which the walls of the vessel are made ; thus it is greater, other circumstances being the same, when the vessel is made of lead than when it is made of aluminium. It also varies, as Campbell and Wood (Phil. Mag. [6], 13, p. 265) have shown, with the time of the day, having a well-marked minimum at about 3 o'clock in the morning : it also varies from month to month. Rutherford (Phys. Rev., 1903, 16, p. 183), Cooke (Phil. Meg., 1903 [6], 6, p. 403) and M'Clennan and Burton (Phys, Rev., 1903, 16, p. 184) have shown that the leak in a closed vessel can be reduced by about 3o% by surrounding the vessel with sheets of thick lead, but that the reduction is not increased beyond this amount, however thick the lead sheets may be. This result indicates that part of the leak is due to a very penetrating kind of radiation, which can get through the thin walls of the vessel but is stopped by the thick lead. A large part of the leak we are describing is due to the presence of radioactive substances such as radium and thorium in the earth's crust and in the walls of the vessel, and to the gaseous radioactive emanations which diffuse from them into the atmosphere. This explains the very interesting effect dis covered by J. Elster and H. Geitel (Phys. Zeit., 1901, 2, p. 56o), that the rate of leak in caves and cellars when the air is stagnant and only renewed slowly is much greater than in the open air.
In some cases the difference is very marked; thus they found that in the cave called the Baumannshohle in the Harz mountains the electricity escaped at seven times the rate it did in the air outside. In caves and cellars the radioactive emanations from the walls can accumulate and are not blown away as in the open air.
The conductivity of normal air arises from several causes; part of it may be due to the presence of radioactive substances in the walls of the vessel in which the gas is contained, or to a little radio active emanation in the gas itself. The conductivity is so small that a mere trace of radioactive substances or of radioactive properties in ordinary matter would be sufficient to account for it. The metal of the containing vessel has certainly a consider able effect on the conductivity of the gas inside; this may, how ever, be due not to an intrinsic radiation of the metal but to a radiation excited by the passage through the metal of a very penetrating radiation for the existence of which there is strong evidence. That the intrinsic radioactivity of the metal and gas cannot be the sole cause of the conductivity is shown by experi ments like that made by M'Clennan (Phil. Mag., v. 24, p. 520, 1912), who measured the conductivity in a hermetically sealed vessel in Canada, England and Scotland and on board a steam ship in the Atlantic ; he found that the conductivity was much the same at the different land stations, and could be represented by the production of about 9 ions per c.c. of the gas per sec., but that the conductivity over the sea was considerably less, and was equivalent to only 6 ions per c.c. per sec. This indicates that some of the conductivity of the gas is due to radiation coming from the land, and that this radiation is cut off by the ocean. This is confirmed by the fact discovered by M'Clennan and McCallum (Phil. Mag., vi. 22, p. 629, 1911), Wulf (Phys. *Tech. xi. p. 811) and Bergwitz (Hahlibakonschrift, Brunswick, 1910) that at the top of high towers the conductivity is less than on the ground; this is what we should expect since the radiation is ab sorbed by the atmosphere. Observations on the conductivity of the air in vessels taken up in balloons by Gockel (Phys. Zeit., x. p. 1909; xii. P. 595, 191 I), Hess (Phys. Zeit., xii. p. 998, 191 1 ), and especially by Kolhorster (Plays. Zeit., xiv. pp. 1066, 1913, Deutsch. Phys. Gesell. V erh., xvi. 14, P. 719, 1914) have brought to light the very interesting fact that the diminution in the conductivity with height ceases when the height exceeds some two kilometres and at greater altitudes is succeeded by an increase in conductivity with altitude.
Kolhorster found that at the height of nine kilometres the con ductivity in a sealed vessel was some ten times that at the surface of the earth. These variations of the conductivity with the height are what would occur if the conductivity were produced by radia tions of two different types (I) a radiation coming from the ground and (2) another coming from the sky. The effects due to (I) would diminish as the height increased while that due to (2) would increase. Estimates of the amount of conductivity due to (2) at the surface of the earth have been made by various observ ers, and it would seem that it may be represented by the produc tion of about 1•5 ions per c.c. per sec. ; as the conductivity at sea level generally requires the production of from 10-20 ions per c.c. per sec. ; much the greater part of the conductivity at the earth's surface must be due to radiation of type 1. Millikan and Bowen give the following results for the conductivity due to radiation of type 2 at different altitudes, the numbers being the number of ions produced per c.c. per sec.: 1.4 at sea-level, 2.6 at 1,600 metres, 4.8 at 1,600 metres, 5.9 at 4,30o metres. Kolhorster (Berlin, Berichte, 1923, p. 366) by making observations at the surface, and in caverns of glaciers on the Jungfrau, measured the absorption of these rays by ice, and found an absorption coefficient of about 2.5 per metre; this is much smaller than that of the y radiation from any known radioactive substance. He found a diurnal variation in the amount of the radiation and suggested that it might be connected with the Milky Way.
Many observations on this radiation have been made by Mil likan and his collaborators (Nature, Jan. 7, 1928), who have meas ured the conductivity in vessels submerged at different depths in two mountain lakes on Mount Whitney. Lake Muir, at an altitude of 11,80o ft., and Arrowhead lake at an altitude of 5,100. These lakes are fed by melted snow so that the water is not likely to contain radioactive matter. It appears from these measurements that the radiation is by no means homogeneous, as the absorption coefficient was greater at the surface of the lake than at the greatest depth at which observations were taken. No trace of the diurnal effect observed by Kolhorster was detected. It was found, too, from observations made in the southern hemisphere on the Andes in Bolivia, that both the character and the amount of the radiation was much the same in the two hemispheres, indicating that the radiation comes pretty uniformly from all parts of the heavens. Applying an expression due to Compton for the connection between the absorption and wave-length it was found that the wave length of the most penetrating radiation was .00038 A; the quantum of energy corresponding to this wave-length is about 32 million volts. This is much greater than the energy associated with any known y radiation. Many suggestions have been made as to its origin. Jeans and Eddington have suggested that it arises from the coalescence of an electron with a positive particle and the conversion of their energy and mass into those of radiation; this would give a radiation more penetrating than that found though it might be degraded by passing through matter. C. T. R. Wilson has suggested the possibility of the radiation being excited by electrons which have acquired energy amounting to millions of volts under the action of something analogous to thunderstorms. This is in accordance with the laws which govern the passage of electrons through gases but Millikan finds no dif ference in the amount of radiation in regions where thunderstorms are frequent and in those where they are rare. We do not know enough at present about these rays to decide either as to their nature or the place of their origin ; it is evident, however, that they raise questions of the greatest interest and importance.
The electrical conductivity of gases in the normal state is, as we have seen, exceedingly small, so small that the investigation of its properties is a matter of considerable difficulty; there are, how ever, many ways by which the electrical conductivity of a gas can be increased so greatly that the investigation becomes compara tively easy. Gases drawn from the neighbourhood of flames, elec tric arcs and sparks, or glowing pieces of metal or carbon are con ductors, as are also gases through which Rontgen or cathode rays or rays of positive electricity are passing; the rays from the radio active metals, radium, thorium, polonium and actinium, produce the same effect, as does also ultra-violet light of exceedingly short wave-length. The gas, after being made a conductor of electricity by any of these means, is found to possess certain properties; thus it retains its conductivity for some little time after the agent which made it a conductor has ceased to act; the conductivity, however, diminishes very rapidly and finally gets too small to be appreciable.
This and several other properties of conducting gas may readily be proved by the aid of the apparatus represented in fig. 1. V is a testing vessel in which an electroscope is placed. Two tubes A and C are fitted into the vessel, A being connected with a water pump, while the f end of C is in the region where the gas is exposed to the agent, which makes it a conductor of electricity.
Let us suppose that the gas is made conducting by Rontgen rays produced by a vacuum tube which is placed in a box, covered except for a window at B with lead so as to protect the electro scope from the direct action of the rays. If a slow current of air is drawn by the water pump through the testing vessel, the charge on the electroscope will gradually leak away. The leak, however, ceases when the current of air is stopped. This result shows that the gas retains its conductivity during the time taken by it to pass from one end to the other of the tube C.
The gas loses its conductivity when filtered through a plug of glass-wool, or when it is made to bubble through water. This can readily be proved by inserting in the tube C a plug of glass wool or a water trap; then if by working the pump a little harder the same current of air is produced as before, it will be found that the electroscope will now retain its charge, showing that the conductivity can, as it were, be filtered out of the gas. • The con ductivity can also be removed from the gas by making the gas traverse a strong electric field. We can show this by replacing the tube C by a metal tube with an insulated wire passing down the axis of the tube. If there is no potential difference between the wire and the tube then the electroscope will leak when a current of air is drawn through the vessel, but the leak will stop if a con siderable difference of potential is maintained between the wire and the tube : this shows that a strong electric field removes the conductivity from the gas.
The fact that the conductivity of the gas is removed by filtering shows that it is due to something mixed with the gas which is removed from it by filtration, and since the conductivity is also removed by an electric field, the cause of the conductivity must be charged with electricity so as to be driven to the sides of the tube by the electric force. Since the gas as a whole is not electrified either positively or negatively, there must be both negative and positive charges in the gas, the amount of electricity of one sign being equal to that of the other. We are thus led to the conclusion that the conductivity of the gas is due to electrified particles being mixed up with the gas, some of these particles having charges of positive electricity, others of negative. These electrified particles are called ions, and the process by which the gas is made a con ductor is called the ionization of the gas. We shall show later that the charges and masses of the ions can be determined, and that the gaseous ions are not identical with those met with in the electrolysis of solutions.
One very characteristic property of conduction of electricity through a gas is the relation between the current through the gas and the electric force which gave rise to it. This relation is not in general that expressed by Ohm's law, which always, as far as our present knowledge extends, expresses the relation for conduction through metals and electrolytes. With gases, on the other hand, it is only when the current is very small that Ohm's law is true. If we represent graphically by means of a curve the relation be tween the current passing between two parallel metal plates separated by ionized gas and the difference of potential between the plates, the curve is of the character shown in fig. 2, when the ordinates rep resent the current and the abscissae the dif ference of potential between the plates.
We see that when the potential difference is very small, i.e., close to the origin, the curve is approximately straight, but that soon the current increases much less rapidly than the potential difference, and that a stage is reached when no appreciable increase of current is produced when the potential difference is increased ; when this stage is reached the current is constant, and this value of the current is called the "saturation" value. When the potential difference approaches the value at which sparks would pass through the gas, the current again increases with the potential difference; thus the curve repre senting the relation between the current and potential difference over very wide ranges of poten tial difference has the shape shown in fig. 3; curves of this kind have been obtained by von Schweidler (Wien. Ber., 1899, 108, p. 273), and J. E. S. Town send (Phil. Mag., 1901 [6], 1, p.
198). We shall discuss later the causes of the rise in the current with large potential differences, when we consider ionization by collision.
The general features of the earlier part of the curve are readily explained on the ionization hypothesis. On this view the Rontgen rays or other ionizing agent acting on the gas between the plates, produces positive and negative ions at a definite rate. Let us sup pose that q positive and q negative ions are by this means pro duced per second between the plates; these under the electric force will tend to move, the positive ones to the negative plate, the negative ones to the positive. Some of these ions will reach the plate, others before reaching the plate will get so near one of the opposite sign that the attraction between them will cause them to unite and form an electrically neutral system ; when they do this they end their existence as ions. The current between the plates is proportional to the number of ions which reach the plates per second. Now it is evident that we cannot go on taking more ions out of the gas than are produced; thus we cannot, when the current is steady, have more than q positive ions driven to the negative plate per second, and the same number of negative ions to the positive. If each of the positive ions carries a charge of e units of positive electricity, and if there is an equal and opposite charge on each negative ion, then the maximum amount of elec tricity which can be given to the plates per second is qe, and this is equal to the saturation current. Thus if we measure the satura tion current, we get a direct measure of the ionization, and this does not require us to know the value of any quantity except the constant charge on the ion. If we attempted to deduce the amount of ionization by measurements of the current before it was sat urated, we should require to know in addition the velocity with which the ions move under a given electric force, the time that elapses between the Iiberation of an ion and its combination with one of the opposite sign, and the potential difference between the plates. Thus if we wish to measure the amount of ionization in a gas we should be careful to see that the current is saturated.
The difference between conduction through gases and through metals is shown in a striking way when we use potential differences large enough to produce the saturation current. Suppose we have got a'potential difference between the plates more than sufficient to produce the saturation current, and let us increase the distance between the plates. If the gas were to act like a metallic con ductor this would diminish the current, because the greater length would involve a greater resistance in the circuit. In the case we are considering the separation of the plates will increase the current, because now there is a larger volume of gas exposed to the rays; there are therefore more ions produced, and as the saturation current is proportional to the number of ions the saturation current is increased. If the potential difference between the plates were much less than that required to saturate the current, then increasing the distance would diminish the current ; the gas for such potential differences obeys Ohm's law and the behaviour of the gaseous resistance is therefore similar to that of a metallic one.
In order to produce the saturation current the electric field must be strong enough to drive each ion to the electrode before it has time to enter into combination with one of the opposite sign. Thus when the plates in the preceding example are far apart, it will take a larger potential difference to produce this current than when the plates are close together. The potential difference required to saturate the current will increase as the square of the distance between the plates, for if the ions are to be delivered in a given time to the plates their speed must be pro portional to the distance between the plates. But the speed is proportional to the electric force acting on the ion; hence the electric force must be proportional to the distance between the plates, and as in a uniform field the potential difference is equal to the electric force multiplied by the distance between the plates, the potential difference will vary as the square of this distance.
The potential difference required to produce saturation will, other circumstances being the same, increase with the amount of ionization, for when the number of ions is large and they are crowded together, the time which will elapse before a positive one combines with a negative will be smaller than when the number of ions is small. The ions have therefore to be removed more quickly from the gas when the ionization is great than when it is small; thus they must move at a higher speed and must there fore be acted upon by a larger force.
When the ions are not removed from the gas, they will increase until the number of ions of one sign which combine with ions of the opposite sign in any time is equal to the number produced by the ionizing agent in that time. We can easily calculate the number of free ions at any time after the ionizing agent has com menced to act.
Thus is constant, so if the gas is uncharged to begin with, will always equal Putting n we have if a. Now the number of ions when the gas has reached a steady state is got by putting t equal to infinity in the preceding equation, and is therefore given by the equation = k= Al(q/a) We see from equation (2) that the gas will not approximate to its steady state until 2kat is large, that is until t is large compared with i/2ka or with a). We may thus take a) as a measure of the time taken by the gas to reach a steady state when exposed to an ionizing agent ; as this time varies inversely as we see that when the ionization is feeble it may take a very considerable time for the gas to reach a steady state. Thus in the case of our atmosphere where the production of ions is only at the rate of about 3o per cubic centimetre per second, and where, as we shall see, a is about 0 it would take some minutes for the ionization in the air to get into a steady state if the ionizing agent were suddenly applied.
We may use equation (I) to determine the rate at which the ions disappear when the ionizing agent is removed. Putting q = o in that equation we get dn/ at= ant.
Hence n = (3), where is the number of ions when t =o. Thus the number of ions falls to one-half its initial value in the time 1/m a. The quantity a is called the coefficient of recombination, and its value for different gases has been determined by Rutherford (Phil. Mag. 1897 [5], 44, P. 422), Townsend (Phil. Trans., 19oo, 193, P. 129), McClung (Phil. Mag., 1902 [6], 3, p. 283), Langevin (Ann. chim. phys. [7], 28, p. 289), Retschinsky (Ann. d. Phys., 1905, 17, p. 518), Hendred (Phys. Rev. 1905, 21, p. 314), Rumelin (Phys. Zeits., ix. p. 657, 1908), Thirkill (Proc. Roy. Soc., 87, p. 477, 1913), Erikson (Phil. Mag., vi. 18 p. 328, 1909; P. 747, 1912). The values of a/e, a being the charge on an ion in electro static measure as determined by these observers for different gases, is given in the following table: The gases in these experiments were carefully dried and free from dust; the apparent value of a is much increased when dust or small drops of water are present in the gas, for then the ions get caught by the dust particles, the mass of a particle is so great compared with that of an ion that they are practically immovable under the action of the electric field, and so the ions clinging to them escape detection when electrical methods are used. Taking e as 4.77X 1 we see that a is about 1.6X i o so that the number of recombinations in unit time between n positive and n negative ions in unit volume is 1.6X The kinetic theory of gases shows that with 2n molecules of air per cubic centimetre the number of collisions per second is 4 X at a temperature of o° C. Thus we see that the number of recombinations between oppositely charged ions is enormously greater than the number of collisions between the same number of neutral molecules. We shall see that the difference in size between the ion and the mole cule is not nearly sufficient to account for the difference between the collisions in the two cases; the difference is due to the force between the oppositely charged ions, which drags ions into col lisions which but for this force would have missed each other.
Several methods have been used to measure a. In one method air, exposed to some ionizing agent at one end of a long tube, is slowly sucked through the tube and the saturation current meas ured at different points along the tube. These currents are pro portional to the values of is at the place of observation : if we know the distance of this place from the end of the tube when the gas was ionized and the velocity of the stream of gas, we can find t in equation (3), and knowing the value of n we can deduce the value of a from the equation where are the values of n at the times respectively. In this method the tubes ought to be so wide that the loss of ions by diffusion to the sides of the tube is negligible. This method does not involve the mobility of the ions, i.e., the speed they acquire under electric forces. Another method which has the same advantage is due to Rumelin. In this the gas is exposed con tinuously to the ionizing agent, while the electric field is applied to the gas by means of a rotating sector and is adjusted so as to be zero during one part of the revolution of the sector and great enough to produce saturation during the remainder. The current sent through the gas by this field is measured and from it the value of a can be calculated. There are other methods which involve the knowledge of the mobility of the ions ; we shall defer the consideration of these methods until we have discussed this question.
In measuring the value of a it should be remembered that the theory of the methods supposes that the ionization is uniform throughout the gas. If the total ionization throughout a gas re mains constant, but instead of being uniformly distributed is con centrated in patches, it is evident that the ions will recombine more quickly in the second case than in the first, and that the value of a will be different in the two cases. This probably ex plains the large values of a obtained by Retschinsky, who ionized the gas by the a rays from radium, a method which produces very patchy ionization.
Variation of a with the Pressure of the Gas.-This question was first investigated by Langevin (Ann. Chem. Phys., 1903, 28, p. 287) who found that at low pressures a was less than at high, thus at the pressure of one-fifth of an atmosphere the value of a for air was about one-fifth of that at atmospheric pressure. He showed, too, that the value of a reached a maximum at a certain pressure-for air about two atmospheres- and fell away fairly rapidly with any further increase in pressure. A very valuable investigation of the effect of pressure on the value of a was made by Thirkill (Proc. Roy. Soc., 88, p. 477, 1913), who showed that for pressures not exceeding one atmosphere a is very approximately a linear function of the pressure, the gases he investigated were air, carbon dioxide, carbon monoxide, sul phur dioxide and nitrous oxide.
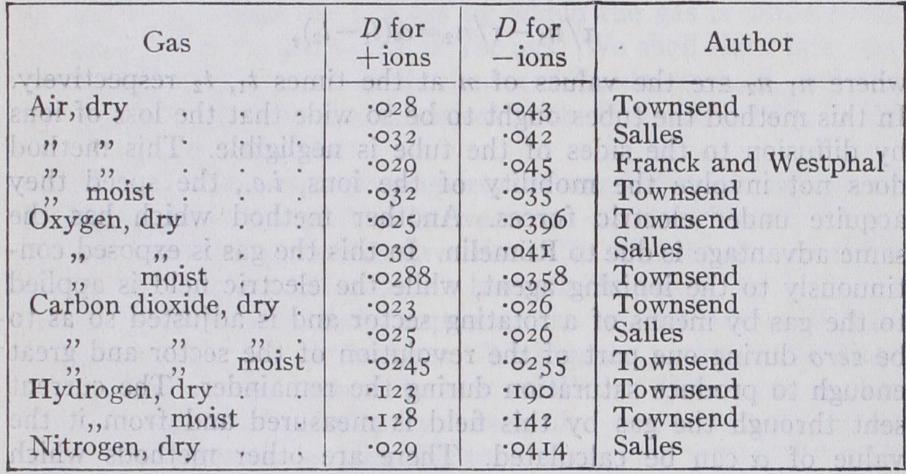
It is interesting to compare with these coefficients the values of D when various gases diffuse through each other. D for hydro gen through air is .634, for oxygen through air .177, for the vapour of isobutyl amide through air -042. We thus see that the velocity of diffusion of ions through air is much less than that of the simple gas, but that it is quite comparable with that of the vapours of some complex organic compounds.
The preceding tables show that the negative ions diffuse more rapidly than the positive, especially in dry gases. The superior mobility of the negative ions was observed first by Zeleny (Phil. Mag., 1898 [5], 46, p. 120), who showed that the velocity of the negative ions under an electric force is greater than that of the positive. It will be noticed that the difference between the mo bility of the negative and the positive ions is much more pro nounced in dry gases than in moist. The difference in the rates of diffusion of the positive and negative ions is the reason why ionized gas, in which, to begin with, the positive and negative charges were of equal amounts, sometimes becomes electrified even although the gas is not acted upon by electric forces. Thus, for example, if such gas be blown through narrow tubes, it will be positively electrified when it comes out, for since the negative ions diffuse more rapidly than the positive, the gas in its passage through the tubes will lose by diffusion more negative than posi tive ions and hence will emerge positively electrified. Zeleny showed that this effect does not occur when, as in carbonic acid gas, the positive and negative ions diffuse at the same rates. Townsend (loc. cit.) showed that the coefficient of diffusion of the ions is the same whether the ionization is produced by Röntgen rays, radioactive substances, ultra-violet light, or elec tric sparks. The ions produced by chemical reactions and in flames are much less mobile ; thus, for example, Bloch (Ann. chim. phys., [8], 4, p. 25) found that for the ions produced by drawing air over phosphorus the value of a/e was between I and 6 instead of over 3,000, the value when the air was ionized by Röntgen rays.
Several methods have been employed to determine these veloci ties. The one most frequently employed is to find the electro motive intensity required to force an ion against the stream of gas moving with a known velocity parallel to the lines of electric force. Thus, of two perforated plane electrodes vertically over each other, suppose the lower to be positively, the upper negatively electrified, and suppose that the gas is streaming vertically down wards with the velocity V; then unless the upward velocity of the positive ion is greater than V, no positive electricity will reach the upper plate. If we increase the strength of the field between the plates, and hence the upward velocity of the positive ion, until the positive ions just begin to reach the upper plate, we know that with this strength of field the ve locity of the positive ion is equal to V. By this method, which has been used by Rutherford, Zeleny, H. A. Wilson and Erikson the ve locity of ions in fields of various strengths has been determined.
The arrangement used by Ze leny is represented in fig. 4. P and Q are square brass plates. They are bored through their centres, and to the openings the tubes R and S are attached, the space between the plates being covered in so as to form a closed box. K is a piece of wire gauze completely covering the opening in Q; T is an insulated piece of wire gauze nearly but not quite filling the opening in the plate P, and connected with one pair of quadrants of an electrometer E. A plug of glass wool G filters out the dust from a stream of gas which enters the vessel by the tube D and leaves it by F ; this plug also makes the velocity of the flow of the gas uniform across the section of the tube. The Rontgen rays to ionize the gas were produced by a bulb at 0, the bulb and coil being in a lead-covered box, with an aluminium window through which the rays passed. Q is connected with one pole of a battery of cells, P and the other pole of the battery are put to earth. The changes in the potential of T are due to ions giving up their charges to it. With a given velocity of air-blast the potential of T was found not to change unless the difference of potential between P and Q exceeded a critical value. The field corresponding to this critical value thus made the ions move with the known velocity of the blast.
Another method which has been employed by Rutherford and McClelland is based on the action of an electric field in destroy ing the conductivity of gas streaming through it. Suppose that BAB, DCD (fig.
5) are a system of parallel plates boxed so that a stream of gas, after flowing between BB, passes between DD without loss of gas in the interval. Suppose the plates DD are insulated, and connected with one pair of quadrants of an elec trometer, by charging up C to a sufficiently high potential we can drive all the positive ions which enter the system DCD against the plates D ; this will cause a deflexion of the electrometer, which in one second will be proportional to the number of posi tive ions which have entered the system in that time. If we charge A up to a high potential, B being put to earth, we shall find that the deflexion of the electrometer connected with DD is less than it was when A and B were at the same potential, because some of the positive ions in their passage through BAB are driven against the plates B. If a is the velocity along the lines of force in the uniform electric field between A and B, and t the time it takes for the gas to pass through BAB, then all the posi tive ions within a distance ut of the plates B will be driven up against these plates, and thus, if the positive ions are equally dis tributed through the gas, the number of positive ions which emerge from the system when the electric field is on will bear to the number which emerge when the field is off the ratio of I — ut/l to unity, where l is the distance between A and B. This ratio is equal to the ratio of the deflexions in one second of the electrometer attached to D, hence the observations of this instru ment give I —ut/l. If we know the velocity of the gas and the length of the plates A and B, we can determine t, and since l can be easily measured, we can find u, the velocity of the positive ion in a field of given strength. By charging A and C negatively instead of positively we can arrive at the velocity of the negative ion. In practice it is more convenient to use cylindrical tubes with coaxial wires instead of the systems of parallel plates, though in this case the calculation of the velocity of the ions from the observations is a little more complicated, inasmuch as the electric field is not uniform between the tubes.
A method which gives very accurate re sults, though it is only applicable in certain cases, is the one used by Rutherford to measure the velocity of the negative ions produced close to a metal plate by the in cidence on the plate of ultra-violet light.
The principle of the method is as follows:—AB (fig. 6) is an insulated horizontal plate of well-polished zinc, which can be moved vertically up and down by means of a screw; it is con nected with one pair of quadrants of an electrometer, the other pair of quadrants being put to earth. CD is a base-plate with a hole EF in it; this hole is covered with fine wire gauze, through which ultraviolet light passes and falls on the plate AB. The plate CD is connected with an alternating current dynamo, which produces a simply-periodic potential difference between AB and CD, the other pole being put to earth. Suppose that at any instant the plate CD is at a higher potential than AB, then the negative ions from AB will move towards CD, and will con tinue to do so as long as the potential of CD is higher than that of AB. If, however, the potential difference changes sign before the negative ions reach CD, these ions will go back to AB. Thus AB will not lose any negative charge unless the distance between the plates AB and CD is less than the distance traversed by the negative ion during the time the potential of CD is higher than that of AB. By altering the distance between the plates until CD just begins to lose a negative charge, we find the velocity of the negative ion under unit electromotive intensity. Suppose the difference of potential between AB and CD is equal to a sin pt, then if d is the distance between the plates the electric intensity is equal to a sin pt/d; if we suppose the velocity of the ion is proportional to the electric intensity; and if u is the velocity for unit electric intensity, the velocity of the negative ion will be ua sin pt/d. Hence if x represent the distance of the ion from AB dx ua = x = ua (I — cospt), if x = o when t = o.
p Thus the greatest distance the ion can get from the plate is equal to 2au/pd, and, if the distance between the plates is gradu ally reduced to this value, the plate AB will begin to lose a nega tive charge ; hence when this happens d = 2au/pd, or u = an equation by means of which we can find u.
Instead of using a harmonically varying field we may by a ro tating commutator apply a constant force for a certain time and then reverse the force taking care that the time it is applied after reversal is longer than the other time. Unless the ion can travel across the distance between the plates before the field is reversed the electrometer will not receive a charge; this gives the means of finding the mobility of the ions.
In this form the method is not applicable when ions of both signs are present. Franck and Pohl (Verb. deutsch. physik. Gesell. 1907, 9 p. 69) have by a slight modification removed this re striction. The modification consists in confining the ionization to a layer of gas below the gauze EF. If the velocity of the positive ions' is to be determined, these ions are forced through the gauze by applying to the ionized gas a small constant electric force acting upwards; if negative ions are required, the constant force is reversed. After passing through the gauze the ions are acted upon by alternating forces as in Rutherford's method. Loeb (Phys. Review, XXI., p. 72o, 1923) has shown that the disturbance of the electric field due to spreading of the lines of force due to the subsidiary field through the gauze may involve serious corrections to the simple theory.
The velocity of the ions produced by the discharge of elec tricity from a fine point was determined by Chattock by an entirely different method. In this case the electric field is so strong and the velocity of the ion so great that the preceding methods are not applicable. Suppose P represents a vertical needle discharging electricity into air, consider the force acting on the ions included between two horizontal planes A, B. If P is the density of the electrification, and Z the vertical com ponent of the electric intensity, F, the resultant force on the ions between A and B, is vertical and equal to Let us suppose that the velocity of the ion is proportional to the electric intensity, so that if w is the vertical velocity of the ions, which are supposed all to be of one sign, w = RZ.
Substituting this value of Z, the vertical force on the ions between A and B is equal to But ffwpdxdy = c, where c, is the current streaming from the point. This current, which can be easily measured by putting a galvanometer in series with the discharging point, is independent of z, the vertical distance of a plane between A and B below the charging point. Hence we have This force mu3t be counterbalanced by the difference of gaseous pressures over the planes A and B ; hence if PB and PA denote respectively the pressures over B and A, we have - PA = z.
Hence by the measurement of these pressures we can determine R, and hence the velocity with which an ion moves under a given electric intensity.
There are other methods of determining the velocities of the ions, but as these depend on the theory of the conduction of electricity through a gas containing charged ions, we shall con sider them in our discussion of that theory.
By the use of these methods it has been shown that the ve locities of the ions in a given gas are the same whether the ionization is produced by Röntgen rays, radioactive substances, ultra-violet light, or by the discharge of electricity from points. When the ionization is produced by chemical action the ions are very much less mobile, moving in the same electric field with a velocity less than one-thousandth part of the velocity of the first kind of ions. On the other hand, as we shall see later, the velocity of the negative ions in flames is enormously greater than that of even the first kind of ion under similar electric fields and at the same pressure. But when these negative ions get into the cold part of the flame, they move sluggishly with velocities of the order of those possessed by the second kind. The results of the various determinations of the velocities of the ions are given in the following table. The velocities are in centimetres per second under an electric force of one volt per centimetre, the pressure of the gas being i atmosphere. V+ denotes the velocity of the positive ion, V — that of the negative. V is the mean velocity of the positive and negative ions.
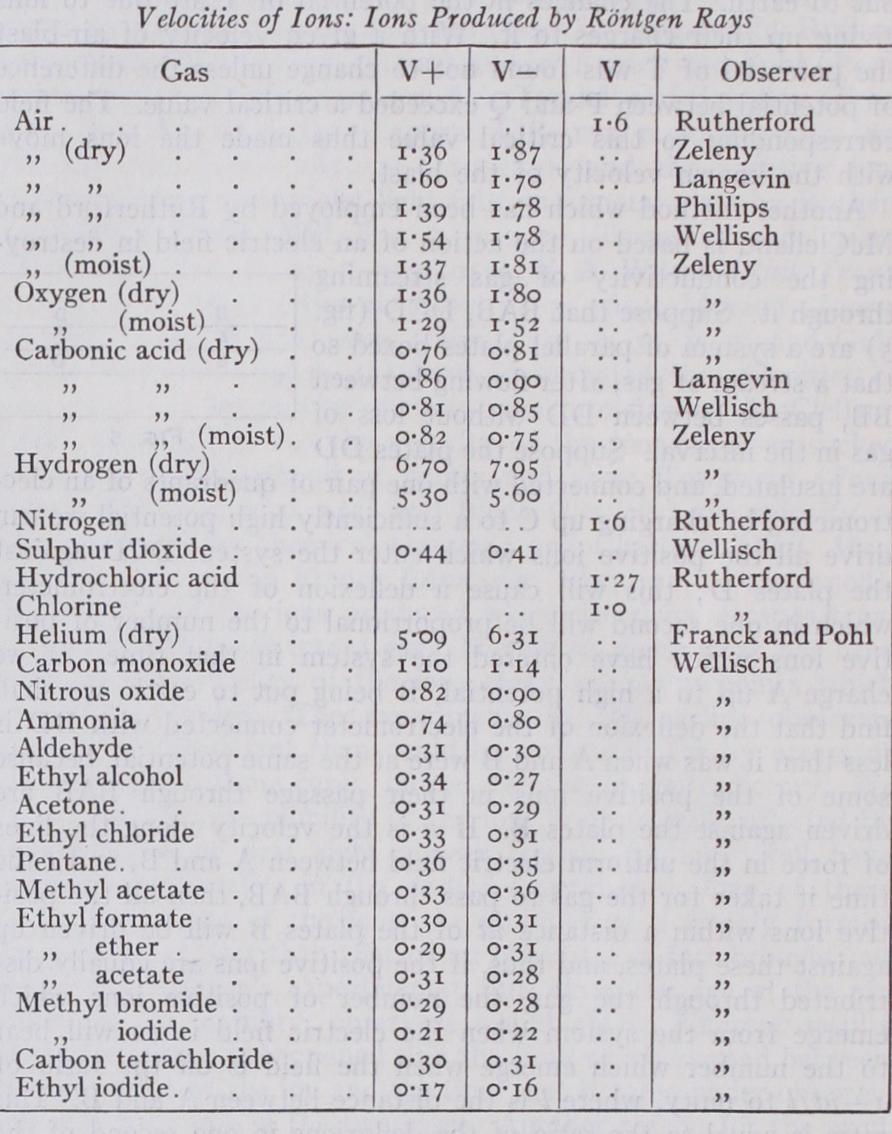
It will be seen from this table that the greater mobility of the negative ions is very much more marked in the case of the lighter and simpler gases than in that of the heavier and more complicated ones ; with the vapours of organic substances there seems but little difference between the mobilities of the positive and negative ions ; indeed in one or two cases the positive seem slightly but very slightly the more mobile of the two. In the case of the simple gases the difference is much greater when the gases are dry than when they are moist. It has been shown by direct experiment that the velocities are directly proportional to the electric force.
The key to the behaviour of the negative ion is the fact that it begins by being an electron and does not unite with a molecule of the gas to form a normal ion until it has made a large number of collisions with the molecules of the gas through which it is pass ing. This number has been determined by Loeb (Phys. Rev., 17, p. 89, 1921 ; Phil. Mag., 43, p. 229, 1922), who finds that it is independent of the pressure of the gas but varies enormously from one gas to another ; thus in pure nitrogen, helium, argon and carbon monoxide in which this number is infinity the electrons never unite with the molecules ; in the number is about three millions, in air about 3o thousand, in oxygen three thousand and in chlorine less than two thousand. When in the electronic state the mobility is very high. Thus Franck found that the mobility of the negative ion in very pure argon was 206, while if 1% of oxygen was added the mobility fell to 1.7 and in pure helium Franck and Gehlhoff found that the mobility of the negative ion was 509. Haines ob tains still larger values for nitrogen and Loeb has shown that these high mobilities vary with the strength of the electric field. The life of the electron is much reduced by the presence of a trace of water vapour.
Most measurements of the mobilities of ions amount to meas uring the time taken by the ion to pass through a given length in the gas ; if the ion begins as an electron the mobility measured will be a mean value depending on the proportion of the time it is an electron to the time of transit. If the pressure is lowered the time in the electronic state is increased, since the number of col lisions the electron makes before leaving this state is unaltered by the change in pressure, while the time between each collision varies inversely as the pressure. The time of transit will be less at low pressures than at high, so that the proportion between the time in the electronic state and the time of transit will vary in versely as the square of the pressure. Thus the high mobility of the electron will produce much greater increase in the mobility at low pressures than at high, and will account for the effects observed by Langevin and Kovarik. It will also account for the fact that the rapid increase of the mobility at low pressures is much more marked in gases which have been carefully dried than in those which contain a trace of water vapour, and that these mobilities depend upon the strength of the electric field.
Effect of Temperature on the Velocity of the Ions.— Phillips (Proc. Roy. Soc., 1906, 78, p. 167) investigated, using Langevin's method, the velocities of the -}- and — ions through air at atmospheric pressure at temperatures ranging from that of boiling liquid air to 41i° C; and R2 are the velocities of the and — ions respectively when the force is a volt per centi metre.
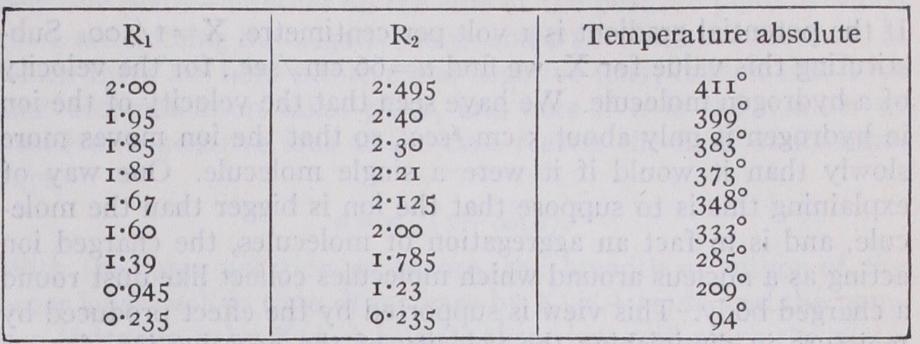
We see that except in the case of the lowest temperature, that of liquid air, where there is a great drop in the velocity, the velocities of the ions are proportional to the absolute temperature ; since the pressure is constant this implies that at constant density the mobility is independent of the temperature. On the hypothesis of an ion of constant size we should, from the kinetic theory of gases, expect the velocity to be proportional to the square root of the absolute temperature, if the charge on the ion did not affect the number of collisions between the ion and the mole cules of the gas through which it is moving. If the collisions were brought about by the electrical attraction between the ions and the molecules, the velocity would be proportional to the absolute temperature. The mobility of ions at high temperatures such as those which occur in flames has been the subject of several experi ments. The first determination was made in 1899 by H. A. Wilson (Phil. Tran., A, 192, P. 499) who measured the mobility of positive ions in flames containing the vapour of alkali metals and found that it was 62 cm./sec. Andrade, in 1912 (Phil. Mag., 6, 23, 865) by a different method obtained the value 2.5 cm./sec. for sodium ions in a flame. H. A. Wilson, in a later investigation (Phil. Trans., A, 216, p. 63, 1916) came to the conclusion that his earlier values were much too high and estimated the true value as 1 cm./sec., which is of the same order as that obtained by Andrade.
The great effect of temperature is also shown in some experi ments of McClelland (Phil. Mag. [5], 46, p. 29) on the velocities of the ions in gases drawn from Bunsen flames and arcs ; he found that these depended upon the distance the gas had travelled from the flame. Thus, the velocity of the ions at a distance of 5.5 cm. from the Bunsen flame when the temperature was C was .23 cm./sec. for a volt per centimetre ; at a distance of r o cm. from the flame when the temperature was 16o° C the velocity was .21 cm./sec.; while at a distance of 14.5 cm. from the flame when the temperature was 105° C the velocity was only .04 cm./sec. If the temperature of the gas at this distance from the flame was raised by external means, the velocity of the ions increased.
We can derive some information as to the constitution of the ions by calculating the velocity with which a molecule of the gas would move in the electric field if it carried the same charge as the ion. From the theory of the diffusion of gases, as developed by Maxwell, we know that if the particles of a gas A are surrounded by a gas B, then, if the partial pressure of A is small, the velocity u with which its particles will move when acted upon by a force Xe is given by the equation Xe u= D (pl/Nl) where D represents the coefficient of inter-diffusion of A into B, and the number of particles of A per cubic centimetre when pressure due to A is pi. Let us calculate by this equation velocity with which a molecule of hydrogen would move hydrogen if it carried the charge carried by an ion, which we prove shortly to be equal to the charge carried by an atom hydrogen in the electrolysis of solutions. Since p1/N1 is pendent of the pressure, it is equal to II/N, where II is the pheric pressure and N the number of molecules in the cubic metre of gas at atmospheric pressure. Now Ne= 1.22 X if is measured in electrostatic units; II= o' and D in this case the coefficient of diffusion of hydrogen into itself, and is equal to If the potential gradient is i volt per centimetre, X=1/3o0. Sub stituting this value for X, we find u= 66 cm./sec., for the velocity of a hydrogen molecule. We have seen that the velocity of the ion in hydrogen is only about 5 cm./sec., so that the ion moves more slowly than it would if it were a single molecule. One way of explaining this is to suppose that the ion is bigger than the mole cule, and is in fact an aggregation of molecules, the charged ion acting as a nucleus around which molecules collect like dust round a charged body. This view is supported by the effect produced by moisture in diminishing the velocity of the negative ion, for, as C. T. R. Wilson (Phil. Trans. p. 289) has shown, moisture tends to collect round the ions, and condenses more easily on the negative than on the positive ion. In connection with the ve locities of ions in the gases drawn from flames, we find other instances which suggest that condensation takes place round the ions. An increase in the size of the system is not, however, the only way by which the velocity might fall below that calculated for the hydrogen molecule, for we must remember that the hydro gen molecule, whose coefficient of diffusion is 1.7, is not charged, while the ion is. The forces exerted by the ion on the other mole cules of hydrogen are not the same as those which would be exerted by a molecule of hydrogen, and as the coefficient of dif fusion depends on the forces between the molecules, the co efficient of diffusion of a charged molecule into hydrogen might be very different from that of an uncharged one.
Wellisch (loc. cit.) has shown that the effect of the charge on the ion is sufficient in many cases to explain the small velocity of the ions, even if there were no aggregation.
Mixture of Gases.—The ionization of a mixture of gases raises some very interesting questions. If we ionize a mixture of two very different gases, say hydrogen and carbonic acid, and investi gate the nature of the ions by measuring their velocities, the question arises, shall we find two kinds of positive and two kinds of negative ions moving with different velocities, as we should do if some of the positive ions were positively charged hydrogen molecules, while others were positively charged molecules of car bonic acid ; or shall we find only one velocity for the positive ions and one for the negative? Many experiments have been made on the velocity of ions in mixtures of two gases, but as yet no evi dence has been found of the existence of two different kinds of either positive or negative ions in such mixtures, although some of the methods for determining the velocities of the ions, espe cially Langevin's, ought to give evidence of this effect, if it existed. The experiments seem to show that the mobilities depend on the nature of the gas through which the ions move but not upon the nature of the ions themselves. Thus Blanc found that the mobility of an ion made in and driven through air was the same as that of an ion made in the air itself.
Grindley and Tyndall (Phil. Mag., 48, p. 711, 1924) show that the mobility through air of ions formed in and was practically the same as that of ordinary air ions. Erikson finds that argon, and H2 ions in air have the same mobility as air ions. Further, Rutherford has shown that the mobility of the heavy "recoil atoms" from radioactive sub stances, which have an atomic weight greater than 200 have in air the same mobility as air atoms. This is important because the radioactive nature of the ions was tested at the end of their path : so that this disposes of the attractive hypothesis that the charge keeps passing from one molecule to another so that how ever the ion may start, it is soon a molecule of the gas through which it is passing. Wellisch made very important experiments on mixed gases, e.g., mixtures of SO2 and and of ethyl ether and air, and found that he could only detect one type of positive and one of negative ions. The only exception to this result seems to be the fact discovered by Erikson that in air positive ions when they are "old," i.e., after some tenths of a second has elapsed since their formation, have only a mobility of about .7 of that of newly formed positive ions, he found no difference between young and old negative ions.
The most important results which have emerged from experi ments on the mobility of the ions are :- 1. The mobility of the ions, especially in the lighter gases, is much less than it would be if the ion consists of a single molecule having the same free path as an uncharged molecule.
2. The mobility of the ions depends only on the gas through which they move, so that though in a mixture of gases there may be ions of different kinds, all the ions of the same sign have the same mobility. An exception to this is the discovery by Erikson that aged ions have a smaller mobility than fresh ones.
3. In the lighter gases the mobility of the negative ions is greater than that of the positive.
4. The mobility of the negative ions is diminished by traces of the vapours of water and various alcohols.
5. For positive ions the product of the mobility and pressure is constant over a very wide range of pressure; for negative ions, however, the product at low pressure rapidly increases as the pressure diminishes.
6. Experiments with heavy ions from radioactive elements show that these have the normal mobility and retain their identity whilst in the electric field.
It is helpful to consider the various conditions which on the kinetic theory of gases would affect the mobility of the ions. The mobility of the ion is proportional to the coefficient of diffusion of the ion through the gas and this coefficient is equal to e is a numerical constant, X the free path of the iron through the gas; in-2 the masses of the ion and molecule respectively and h=RT/2 where T is the absolute temperature and R the gas con stant. First consider the effect of the electric charge on the free path, supposing for the moment that the mass of the ion is the same as that of a molecule. The attraction between an ion and a molecule will in consequence of the charge be greater than that between uncharged molecules ; the ion and the molecules will be dragged together and the free path of the ion less than that of the molecule. Thus X will be less for the ion than for the mole cule and the coefficient of diffusion less. If X' is the free path of the ion, X that of the uncharged molecule, w the work required to separate an ion from a molecule with which it is in contact, we can show that if the form between the ion and the molecule varies inversely as the fifth power of the distance when a is a numerical constant. We see from this expression that if we are to explain the slow diffusion of the ion by the charge alone, w must be large compared with RT, i.e., the work required to separate an ion from a molecule must be large compared with the kinetic energy of a molecule due to thermal agitation. It follows, however, from the principles of thermodynamics that in this case the ions will unite with the molecules and form aggre gates, and thus that any considerable diminution in the free path is inconsistent with the ions being monomolecular.
Let us turn now to the effect of mass upon the mobility of the ion; we see from the for the coefficient of diffusion that the mobility is proportional to Thus when the mass of the ion, is one, two, three—or an infinite number of times that of the molecule the mobilities are in the ratio 1.41, 1.22, 1.15--1. Though these differences are not very large they are much greater than is consistent with the experi mental fact that there is only one mobility for all positive and another for all negative in the same gas. While the mobility of a light ion through a heavy gas will be much greater than that of one formed by a molecule of this gas, thus from the formula the mobility of a hydrogen ion through methyl iodide would be six times that of a methyl iodide ion. We are forced to the conclusion that the ions cannot remain unaltered during their path through the gas, but must pass through various phases in which they have different mobilities, and that the mobility measured by the usual methods is an average value and not its value in any particular phase.
Thus is always greater than unity, and the value of the ratio increases from unity to infinity as (3 increases from zero to infinity. As j3 does not involve either q or I, the ratio of to is independent of the strength of the current and of the intens ity of the ionization.
No general solution of equation (8) has been found when is not equal to but we can get an approximation to the solution when q is constant. The equations (1), (2), (3), (4) are satisfied by the values k1n1Xe= k1 I, k1+k2 = k2 I, ki±k2 X= I • k ql ( -{- 2) These solutions cannot, however, hold right up to the surface of the plates, for across each unit of area, at a point P, positive ions pass in unit time, and these must all come from the region between P and the positive plate. If X is the distance of P from this plate, this region cannot furnish more than qX positive ions, and only this number if there are no recombinations. Hence the solution cannot hold when qX is less than or where X is less than Similarly the solution cannot hold nearer to the negative plate than the distance The force in these layers will be greater than that in the middle of the gas, and so the loss of ions by recombination will be smaller in comparison with the loss due to the removal of the ions by the current. If we assume that in these layers the loss of ions by recombination can be neglected, we can by the method of the next article find an expression for the value of the electric force at any point in the layer. This, in conjunction with the value Xo= (a I for the gas outside the layer, will give the q e(ki-l-k2)-l-- k2) value of X at any point between the plates. It follows from this hence so that the potential falls at the electrodes are proportional to the squares of the velocities of the ions. The change in potential across the layers is proportional to the square of the current, while the potential change between the layers is proportional to the current, the total potential difference between the plates is the sum of these changes, hence the relation between V and i will be of the form V = Aid-BP.
Though we are unable to obtain a general solution of the equa tion (8), there are some very im portant special cases in which that equation can be solved with out difficulty. We shall consider two of these, the first being that when the current is saturated. In this case there is no loss of ions by recombination, so that using the same notation as before we have where C is a quantity to be determined by the condition = V, where V is the given potential difference between 0 the plates. When the force is a minimum dX/dx = o, hence at this point x= ,l —x = • kl+k2 Hence the ratio of the distances of this point from the positive and negative plates respectively is equal to the ratio of the veloci ties of the positive and negative ions.
Conduction When All the Ions Are of One Sign. The Space Charge Effect.—There are many important cases in which the ions producing the current come from one electrode or from a thin layer of gas close to the electrode, no ionization occurring in the body of the gas or at the other electrode. Among such cases may be mentioned those where one of the electrodes is raised to incandescence while the other is cold, or when the negative elec trode is exposed to ultra-violet light. In such cases if the elec trode at which the ionization occurs is the positive electrode, all the ions will be positively charged, while if it is the negative electrode the ions will all be charged negatively. The theory of this case is exceedingly simple. Suppose the electrodes are par allel planes at right angles to the axis of x; let X be the electric force at a distance x from the electrode where the ionization oc curs, n the number of ions (all of which are of one sign) at this place per cubic centimetre, k the velocity of the ion under unit electric force, e the charge on an ion, and i the current per unit area of the electrode. Then we have dX = 4irne, and if u is the dx kX dX velocity of the ion neu = i. But u = kX, hence we have dx = and since the right hand side of this equation does not depend upon x, we get = ix-+C, where C is a constant to be de termined. If 1 is the distance between the plates, and V the po tential difference between them, To show that for small currents C is small compared with il, consider the case when the ionization is confined to a thin layer, thickness d close to the electrode; in that layer let be the value of n, then we have q = If be the value of X when x=o, = i, and Since a/8irke is, as we have seen, less than unity, C will be small compared with il, if i/(eq+-i/d) is small compared with 1. If is the saturation current, q = I so that the former expression if i is small compared with this expression is small compared with d, and therefore a fortiori compared with 1, so that we are justified in this case in using equation (i).
From equation (I) we see that the current increases as the square of the potential difference. Here an increase in the poten tial difference produces a much greater percentage increase than in conduction through metals, where the current is proportional to the potential difference. When the ionization is distributed through the gas, we have seen that the current is approximately proportional to the square root of the potential, and so increases more slowly with the potential difference than currents through metals. From equation (I) the current is inversely proportional to the cube of the distance between the electrodes, so that it falls off with great rapidity as this distance is increased. We may note that for a given potential difference the expression for the current does not involve q, the rate of production of the ions at the electrode ; in other words, if we vary the ionization the current will not begin to be affected by the strength of the ionization until this falls so low that the current is a considerable fraction of the saturation current. For the same potential difference the current is proportional to k, the velocity under unit electric force of the ion which carries the current. As the velocity of the nega tive ion is greater than that of the positive, the current when the ionization is confined to the neighbourhood of one of the elec trodes will be greater when that electrode is made cathode than when it is anode. Thus the current will appear to pass more easily in one direction than in the opposite.
Since the ions which carry the current have to travel all the way from one electrode to the other, any obstacle which is im pervious to these ions will, if placed between the electrodes, stop the current to the electrode where there is no ionization. A plate of metal will be as effectual as one made of a non-conductor, and thus we get the remarkable result that by interposing a plate of an exceIIent conductor like copper or silver between the electrode we can entirely stop the current. This experiment can easily be tried by using a hot plate as the electrode at which the ionization takes place : then if the other electrode is cold the current which passes when the hot plate is cathode can be entirely stopped by interposing a cold metal plate between the electrodes.
A very interesting case of the space charge effect is when, as above, the ions are produced close to one electrode or are emitted by it and the pressure of the gas is so low that the motion of the ions is not affected by the presence of the gas. This includes the very important case where currents are carried through a vacuum by the electrons emitted from an incandescent electrode.
If V be the potential difference between a point P in the gas and this electrode, n the number of ions per cc. at P m the mass and e the charge on the ion, x the distance of P from the electrode. Then A complete solution of this equation can be obtained without difficulty; the expressions for this solution are, however, some what complicated, and we shall confine ourselves to the special case when the current passing is small compared with the satura tion current, in this case dV/dx vanishes at the electrode and the solution of (6) is V={9i(m/u)4}* • x (7) or i the current sent by a potential difference V, when 1 is the distance between the electrode is given by Thus the current produced by a given potential difference is inde pendent of the rate at which the electrons are emitted from the electrode ; this is, however, only true when the current is far from saturation.
2 We see from equation (3) that dxZ therefore n are in finite when x=o, so that there is a great accumulation of ions close to this electrode.
The "space charge effect" has been the subject of most impor tant investigations by Langmuir, to whom its development is mainly due.
Methods of Counting the Number of Ions.—The detection of the ions and the estimation of their number in a given volume is much facilitated by the property they possess of promoting the condensation of water-drops in dust-free air supersaturated with water vapour. If such air contains no ions, then it requires about an eightfold supersaturation before any water-drops are formed; if, however, ions are present C. T. R. Wilson (Phil. Trans., 189, p. 265) has shown that a sixfold supersaturation is sufficient to cause the water vapour to condense round the ions and to fall down as raindrops. The absence of the drops when no ions are present is due to the curvature of the drop combined with the surface tension causing, as Lord Kelvin showed, the evaporation from a small drop to be exceedingly rapid, so that even if a drop of water were formed the evaporation when it was small would be so great that it would rapidly evaporate and disappear. It has been shown, however (J. J. Thomson, Application of Dynamics to Physics and Chemistry, p. 164 ; Conduction of Electricity through Gases, and ed. p. 179), that if a drop of water is charged with electricity the effect of the charge is to diminish the evapora tion; if the drop is below a certain size the effect of the charge in promoting condensation more than counterbalances the effect of the surface tension in promoting evaporation. Thus the electric charge protects the drop in the most critical period of its growth.
The effect is easily shown experimentally by taking a bulb con nected with a piston arranged so as to move with great rapidity. When the piston moves so as to increase the volume of the air contained in the bulb the air is cooled by expansion, and if it was saturated with water vapour before it is supersaturated after the expansion. By altering the throw of the piston the amount of supersaturation can be adjusted within very wide limits. Let it be adjusted so that the expansion produces about a sixfold super saturation; then if the gas is not exposed to any ionizing agents very few drops (and these probably due to the small amount of ionization which we have seen is always present in gases) are formed. If, however, the bulb is exposed to strong Röntgen rays expansion produces a dense cloud which gradually falls down and disappears. If the gas in the bulb at the time of its exposure to the Röntgen rays is subject to a strong electric field hardly any cloud is formed when the gas is suddenly expanded. The electric field removes the charged ions from the gas as soon as they are formed so that the number of ions present is greatly reduced. This experiment furnishes a very direct proof that the drops of water which form the cloud are only formed round the ions.
This method gives us an exceedingly delicate test for the pres ence of ions, for there is no difficulty in detecting ten or so rain drops per cubic centimetre; we are thus able to detect the presence of this number of ions. This result illustrates the enormous dif ference between the delicacy of the methods of detecting ions and those for detecting uncharged molecules; we have seen that we can easily detect ten ions per cubic centimetre, but there is no known method, spectroscopic or chemical, which would enable us to detect a billion times this number of uncharged mole cules. The formation of the water-drops round the charged ions gives us a means of counting the number of ions present in a cubic centimetre of gas; we cool the gas by sudden expansion until the supersaturation produced by the cooling is sufficient to cause a cloud to be formed round the ions, and the problem of finding the number of ions per cubic centimetre of gas is thus reduced to that of finding the number of drops per cubic centimetre in the cloud. Unless the drops are very few and far between we cannot do this by direct counting; we can, however, arrive at the result in the following way. From the amount of expansion of the gas we can calculate the lowering produced in its temperature and hence the total quantity of water precipitated. The water is precipitated as drops, and if all the drops are the same size the number per cubic centimetre will be equal to the volume of water deposited per cubic centimetre, divided by the volume of one of the drops. Hence we can calculate the number of drops if we know their size, and this can be determined by measuring the velocity with which they fall under gravity through the air.
Stokes showed that the force required to drive a drop of water with a velocity v through a continuous fluid is equal to 67rp.av where a is the radius of the drop and /./. the viscosity of the fluid. Cunningham (Proc. Roy. Soc., F3, A. p. 357) showed that this expression requires modification when the drop moves through a gas in which the mean free path of the molecules is comparable with the radius of the drop. He shows that the factor must —1 be replaced by 6orµaC I + I where 1 is the mean free path of the molecules. Since 1 varies inversely as the pressure, p, of the gas the factor is of the form 67rµa (I +—) where B is a Pa constant. Milliken, assuming an expression of this form, deter mined the value of B by experiment. When the drop falls under gravity the force is when p is the density of the drop and a that of the gas. Since this is equal to V multiplied by a known function of a, if we measure V we can deduce the value of a.
Drops of water, as we have seen, condense more easily on nega tive than on positive ions. It is possible, therefore, to adjust the expansion so that a cloud is formed on the negative but not on the positive ions. Wilson arranged the experiments so that such a cloud was formed between two horizontal plates which could be maintained at different potentials. The charged drops between the plates were acted upon by a uniform vertical force which affected their rate of fall. Let X be the vertical electric force, e the charge on the drop, the rate of fall of the drop when this force acts, and v the rate of fall due to gravity alone. Then since the rate of fall is proportionate to the force on the drop, if a is the radius of the drop, and p its density, then Thus if X, v, are known e can be determined. Wilson by this method found that e was 3.1 X electrostatic units. A few of the ions carried charges 2e or 3e.
Townsend has used the following method to compare the charge carried by a gaseous ion with that carried by an atom of hydrogen in the electrolysis of solution. We have u/D = Ne/jr, where D is the coefficient of diffusion of the ions through the gas, u the velocity of the ion in the same gas when acted on by unit electric force, N the number of molecules in a cubic centimetre of the gas when the pressure is it dynes per square centimetre, and e the charge in electrostatic units. This relation is obtained on the hypothesis that N ions in a cubic centimetre produce the same pressure as N uncharged molecules.
We know the value of D from Townsend's experiments and the values of u from those of Zeleny. We get the following values for Ne X Since 1.22 cubic centimetres of hydrogen at the temperature I 5 ° C and pressure 76o mm. of mercury are liberated by the passage through acidulated water of one electromagnetic unit of electricity or 3 X electrostatic units, and since in one cubic centimetre of the gas there are 2.46 N atoms of hydrogen, we have, if E is the charge in electrostatic units, on the atom of hydrogen in the electrolysis of solutions The mean of the values of Ne in the preceding table is 1.24X I olo Hence we may conclude that the charge of electricity carried by a gaseous ion is equal to the charge carried by the hydrogen atom in the electrolysis of solutions. The values of Ne for the different gases differ more than we should have expected from the prob able accuracy of the determination of D and the velocity of the ions : Townsend (Proc. Roy. Soc. 8o, p. 207) has shown that when the ionization is produced by Röntgen rays some of the positive ions carry a double charge and that this accounts for the values of Ne being greater for the positive than for the negative ions. Since we know the value of e, viz., 4.77 X I and, also Ne, = I.24 X I we find N the number of molecules in a cubic centimetre of gas at standard temperature and pressure to be equal to 2.6 X I This method of obtaining N is the only one which does not involve any assumption as to the shape of the molecules and the forces acting between them.
Another method of determining the charge carried by an ion has been employed by Rutherford (Proc. Roy. Soc. 81, pp. 141, 162), in which the positively electrified particles emitted by ra dium are made use of. The method consists of : (1) Counting the number of a particles emitted by a given quantity of radium in a known time. (2) Measuring the electric charge emitted by this quantity in the same time. To count the number of the a particles the radium was so arranged that it shot into an ionization cham ber a small number of a particles per minute; the interval between the emission of individual particles was several seconds. When an a particle passed into the vessel it ionized the gas inside and so greatly increased its conductivity; thus, if the gas were kept exposed to an electric field, the current through the gas would suddenly increase when an a particle passed into the vessel. Although each a particle produces about 3o thousand ions, this is hardly large enough to produce the conductivity appreciable with out the use of very delicate apparatus; to increase the conduc tivity Rutherford took advantage of the fact that negative ions, when exposed to a strong electric field, produce other ions by collision against the molecules of the gas through which they are moving. By suitably choosing the electric field and the pressure in the ionization chamber, the 30,00o ions produced by each a particle can be multiplied to such an extent that an appreciable current passes through the ionization chamber on the arrival of each a particle. An electrometer placed in series with this vessel will show by its deflection when an a particle enters the chamber, and by counting the number of deflections per minute we can determine the number of a particles given out by the radium in that time. Another method of counting this number is to let the particles fall on a phosphorescent screen, and count the number of scintillations on the screen in a certain time. Rutherford has shown that these two methods give concordant results.
The charge of positive electricity given out by the radium was measured by catching the a particles in a Faraday cylinder placed in a very highly exhausted vessel, and measuring the charge per minute received by this cylinder. In this way Rutherford showed that the charge on the a particle was 9.4X 1 electrostatic units. Now e/m for the a particle = 5 X and there is evidence that the a particle is a charged atom of helium; since the atomic weight of helium is 4 and elm for hydrogen is I it follows that the charge on the helium atom is twice that on the hydrogen, so that the charge on the hydrogen atom is 4.7 X I electrostatic units.
Calculation of the Mass of the Ions at Low Pressures.— Although at ordinary pressures the ion seems to have a very com plex structure and to be the aggregate of many molecules, yet we have evidence that at very low pressures the structure of the ion, and especially of the negative one, becomes very much sim pler. This evidence is afforded by determination of the mass of the atom. We can measure the ratio of the mass of an ion to the charge on the ion by observing the deflections produced by mag netic and electric forces on a moving ion. If an ion carrying a charge e is moving with a velocity v, at a point where the mag netic force is H, a mechanical force acts on the ion, whose direc tion is at right angles both to the direction of motion of the ion and to the magnetic force, and whose magnitude is evHsin9 where 0 is the angle between v and H. Suppose then that we have an ion moving through a gas whose pressure is so low that the free path of the ion is long compared with the distance through which it moves whilst we are experimenting upon it; in this case the motion of the ion will be free, and will not be affected by the presence of the gas.
Since the force is always at right angles to the direction of mo tion of the ion, the speed of the ion will not be altered by the action of this force; and if the ion is projected with a velocity v in a direction at right angles to the magnetic force, and if the magnetic force is constant in magnitude and direction, the ion will describe a curve in a plane at right angles to the magnetic force. If p is the radius of curvature of this curve, m the mass of the ion, must equal the normal force acting on the ion, i.e. it must be equal to Hev, or p = mv/He. Thus the radius of curva ture is constant; the path is therefore a circle, and if we can measure the radius of this circle we know the value of mv/He. In the case of the rapidly moving negative ions projected from the cathode in a highly exhausted tube, which are known as cathode rays, the path of the ions can be readily determined since they make many substances luminous when they impinge against them. Thus by putting a screen of such a substance in the path of the rays the shape of the path will be determined. Let us now suppose that the ion is acted upon by a vertical electric force X and is free from magnetic force, if it be projected with a hori zontal velocity v, the vertical deflection y after a time t is 1 X or if t is the horizontal distance travelled over by the ions in this time we have, since l = vt, Thus if we measure y and l we can deduce From the effect of the magnetic force we know e/mv. Combining these results we can find both e/m and v.
The method by which this de termination is carried out in prac tice is illustrated in fig. 9. The cathode rays start from the elec trode C in a highly exhausted tube, pass through two small holes in the plugs A and B, the holes being in the same horizontal line. Thus a pencil of rays emerging from B is horizontal and produces a bright spot at the far end of the tube. In the course of their journey to the end of the tube they pass between the horizontal plates E and D, by connecting these plates with an electric battery a vertical electric field is produced between E and D and the phosphorescent spot is deflected vertically. By measuring this deflection we determine The rays are also exposed to a uniform magnetic field, the lines of magnetic force being vertical. The magnetic force makes the rays describe a circle in a horizontal plane, and by measuring the horizontal deflection of the phos phorescent patch at the end of the tube we can determine the radius of this circle, and hence the value of e/mv. From the two observations thus obtained the value of e/m and v can be calculated.
By these methods J. J. Thomson determined the value of e/m for the negative ions produced when ultra-violet light falls on a metal plate, as well as for the negative ions produced by an in candescent carbon filament in an atmosphere of hydrogen (Phil. Mag. [5] , P. 547) as well as for the cathode rays. It was found that the value of e/m for the negative ions was the same in all these cases, and that it was a constant quantity independent of the nature of the gas from which the ions are produced and the means used to produce them. It was found, too, that this value was more than a thousand times the value of e/M, where e is the charge carried by an atom of hydrogen in the electrolysis of solu tions, and M the mass of an atom of hydrogen. We have seen that this charge is the same as that carried by the negative ion in gases; thus since e/m is more than a thousand times e/M, it fol lows that M must be more than a thousand times m. Thus the mass of the negative ion is exceedingly small compared with the mass of the atom of hydrogen, the smallest mass recognized in chemistry. The production of negative ions thus involves the splitting up of the atom, as from a collection of atoms something is detached whose mass is less than that of a single atom. It is important to notice in connection with this subject that an entirely different line of argument, based on the Zeeman effect (q.v.), leads to the recognition of negatively electrified particles for which e/m is of the same order as that deduced from the consideration of purely electrical phenomena. These small negatively electrified particles are called electrons. The latest determinations of e/m for electrons available are given in the table in the next column.
It follows from electrical theory that when the electrons are moving with a velocity comparable with that of light their masses increase rapidly with their velocity. This effect has been detected by Kauffmann (Gott. Nach., Nov. 8, Igor), who used the electrons shot out from radium, some of which move with velocities only a few per cent less than that of light. Other experiments on this point have been made by Bucherer (Ann. der Phys. 28, p. 513). Conductivity Produced by Ultraviolet Light. (See