Geometrical Problems 46
line, radius, ab and center
GEOMETRICAL PROBLEMS 46. There are certain problems of geomet rical construction which it is essential that the intelligent draftsman should know. We shall now present some of the,' more common of these problems.
To Bisect a Given Straight Line Let AB, Fig. 25, be the given line. With B as a center, and a radius greater than one-half the of the line, describe an arc above AB, and another below; and with the same radius, and A as a center, draw two other arcs above and below AB, cutting the first two arcs at the points 1 and 2. A straight line joining 1 with 2 will divide AB in two equal parts, bisecting it at point C.

right angles, and accuracy thereby become easier to obtain if the radius used is taken (by eye) between two-thirds and three-quarters the length of AB.
To Bisect a Given Angle In Fig. 26, let AB and BC form the given angle at B. With B as center, and any radius, strike an arc cutting AB and BC in points 1 and 2. With point 1 as center, and any radius greater than one-half the distance from 1 to 2, strike an arc; and with the point 2 as center, and the same radius, draw another arc, cutting the one just drawn, in point 3. A line joining point B with point 3 is the bisecting line required.
NOTE—To test the exactness of the work, take the dividers, set one point at 4, open to point 1, then see if this span is the same as that from 4 to 2.
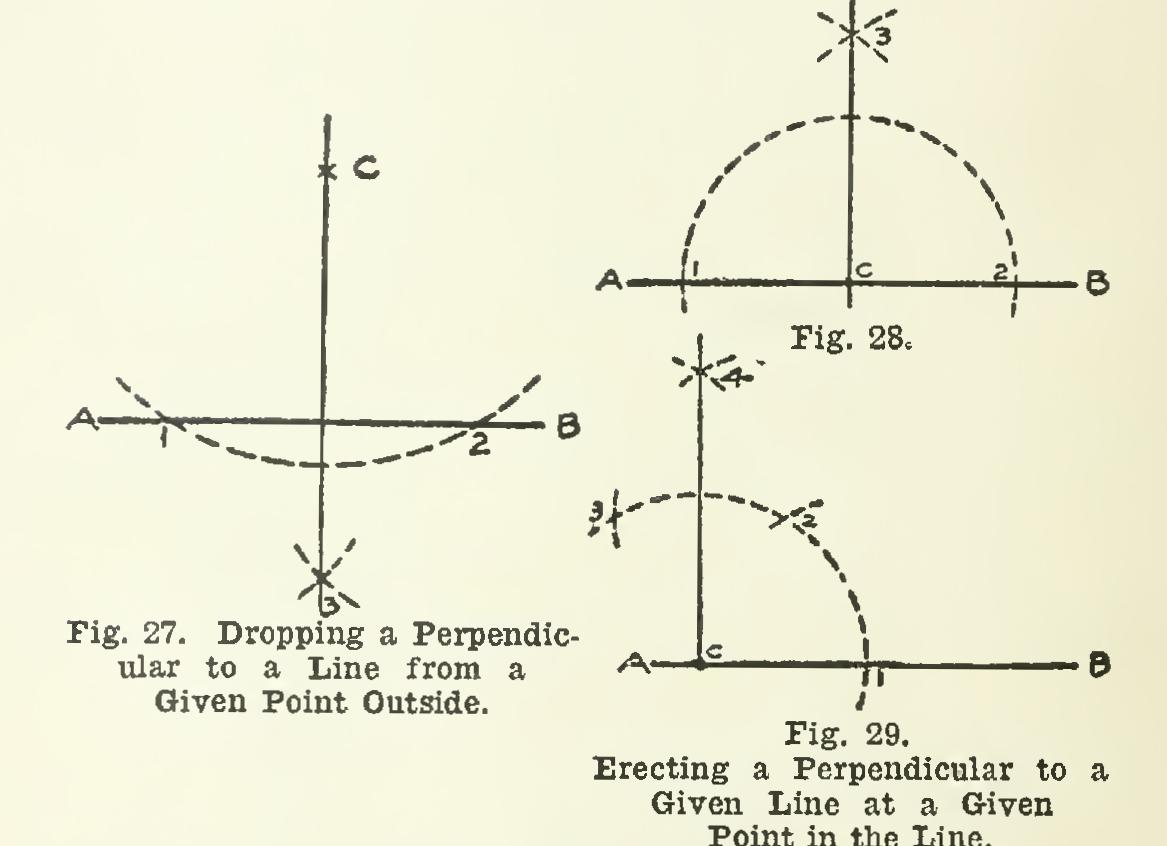
To Draw a Perpendicular to a Given Line from a Given Point Outside Let AB, Fig. 27, be the given line, and c the given point. With the point c as a center, and any sufficiently large radius, describe an arc cutting the given line in two points, as 1 and 2. Then, with 1 as center, and any convenient radius, strike an arc (preferably on the other side of the line from point c); and with center 2, and the same radius, strike another arc, inter secting the first one in point 3. Connect the point 3 with point c, and this will be the per pendicular required.
To Erect a Perpendicular to a Given Line at a Given Point on the Line When the given point is not very near either end of the line.
Let AB, Fig. 28, represent the given line, and c the given point. With c as center, and any radius, strike an arc cutting AB in points 1 and 2; then, with 1 and 2 as centers, and any suitable radius, strike arcs intersecting at 3. A line drawn from 3 to c will be the desired per pendicular.