Arches - Centers - Windows and Door-Heads

Next in point of time, but by far the most graceful in form, is the pointed arch, which is essentially the middle age style, and is capable of almost endless variety. Just where it originated is hard to tell, as recent discoveries have shown that it was used many centuries ago in Assyria. The greater or less acuteness of the pointed arch depends on the position of the centers from which the flanks are struck.

The Lancet

arch indicates the style called "Early English," and is drawn as shown in Fig. 63. D C is the given span; bi sect DC in E, make CB and DA equal to EC or ED ; on B as center with DB as radius, describe the arc DF, and on A as center, describe the arc CF, and the arch is complete.

Equilateral

arch (Fig. 64) is known as the Gothic Arch, and is constructed as follows : The radius with which the arcs are struck being equal to the span of the arch, and the centers being the imposts ; and thus, the crown and the imposts being united, an equilateral triangle is formed. During the time that the Gothic arch was mostly used the Ogee arch (Fig. 65) was also occasionally used.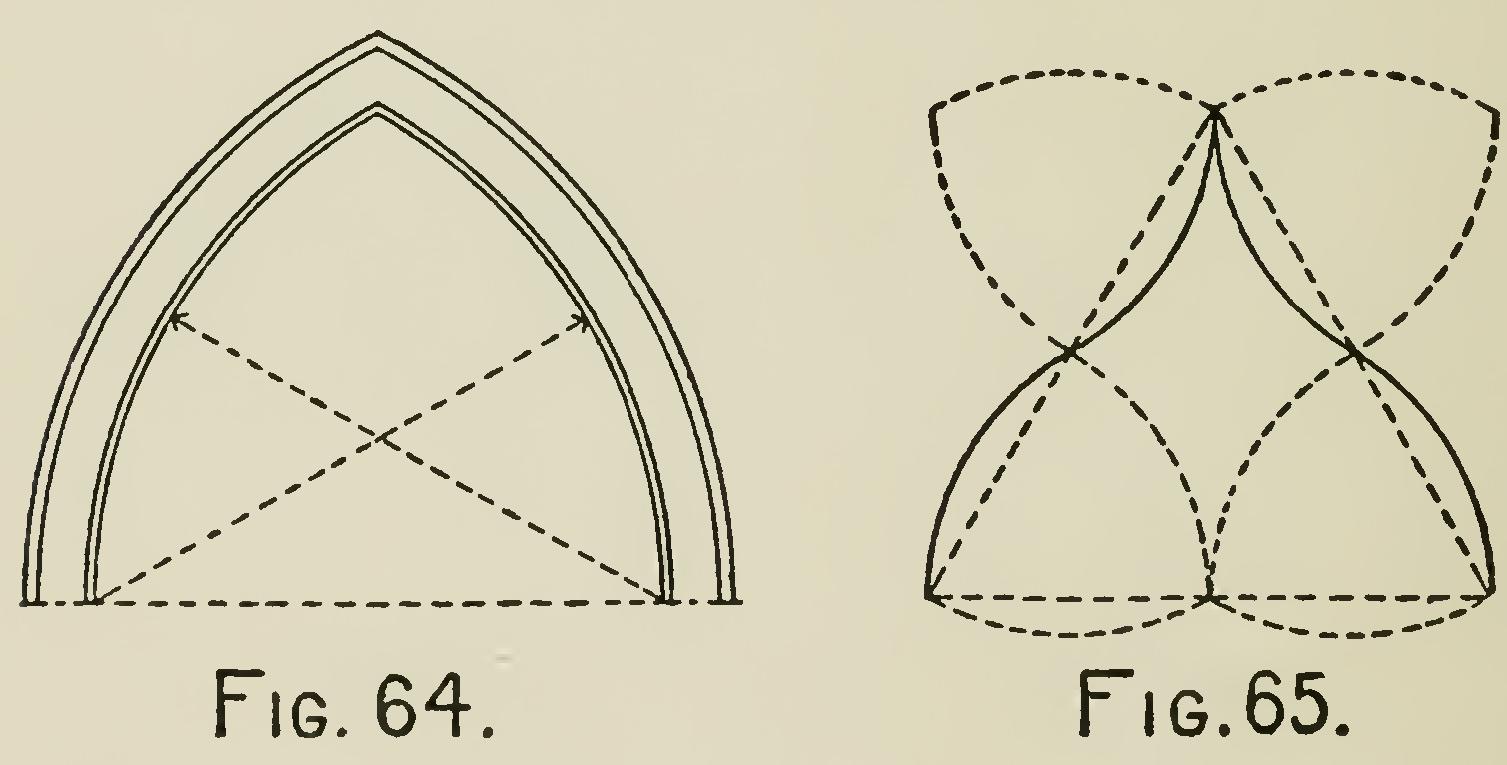

A

little later on we find the Tudor arches, or four-centered arches (Fig. 66), in which two of the centers are on the springing line and two below it. The arches at the later period of this style became flatter and flatter, and this forms one of the features of Debased Gothic, when the beautiful and graceful forms of that style gradu ally decayed and for a time were lost. Happily in the present century there has been a gradual revival of the Gothic style, and works are now being produced which bid fair to rival in beauty of form and in principle of construction t h e marvelous buildings of the middle ages.

From the examples given the workman will be able to lay out any of the usual arches re quired in building.

There are com binations, however, of these curves which the carpenter may be called upon to construct, such as the ones given here with.

Fig. 67 is the elementary study upon which the subsequent figure is based. Having drawn the circle, describe on the diameter two opposite semi-circles, meeting at the center, a.

Divide one of these into six equal parts, and set off one of these sixths from i to n. Draw an, and divide it into four equal parts. From the middle point of a n draw a line passing through the center of the semi-circle, and cutting it in c. From c set off on this line the length of one of the fourths of a n. This point and the two in a n will be the centers for the interior curves.

Fig. 68 is the further working out of this ele mentary figure. It is desirable that a larger circle should be drawn. Then, when the figure has been carried up to the stage shown in the last, all the rest of the curves will be drawn from the same centers.

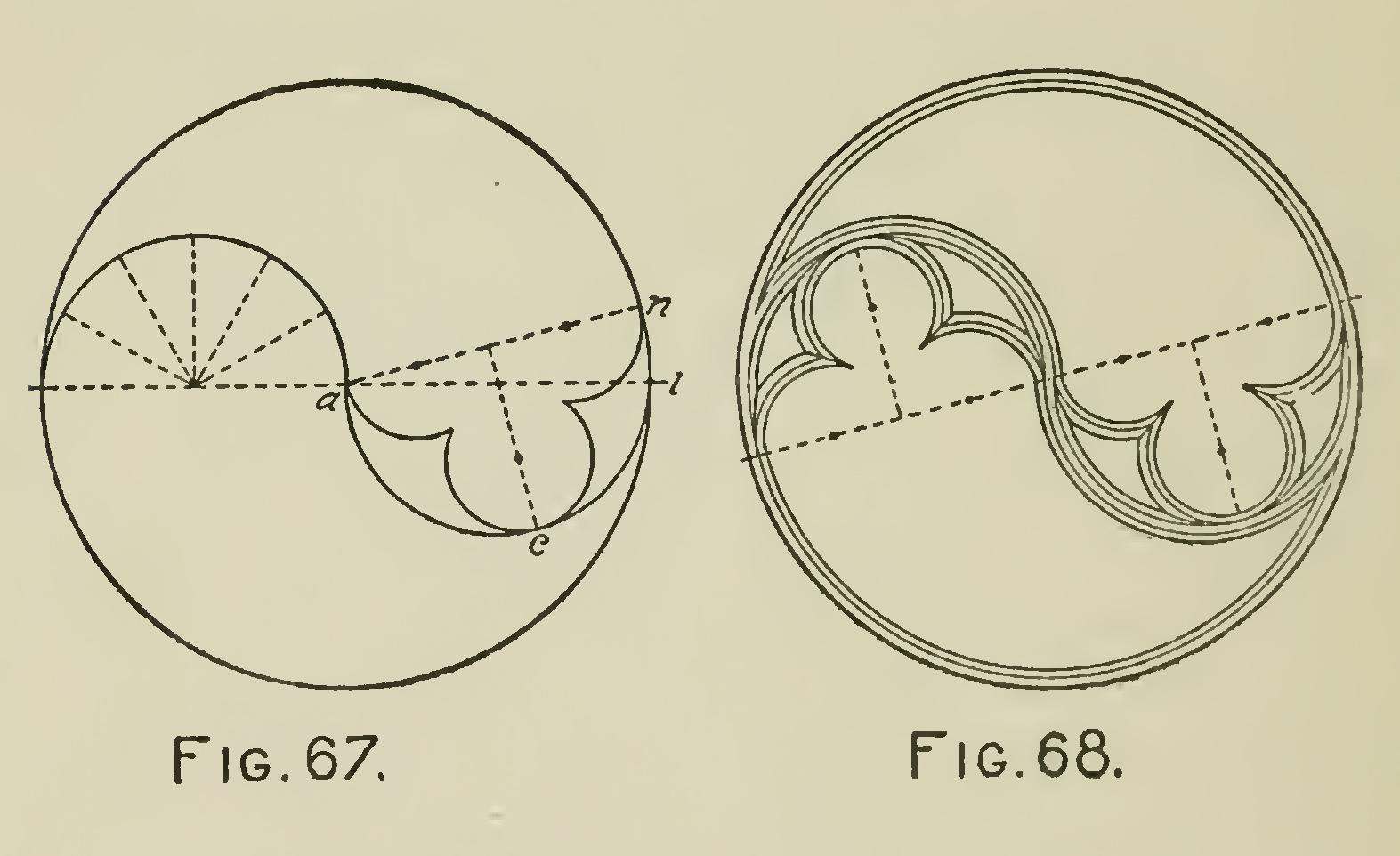
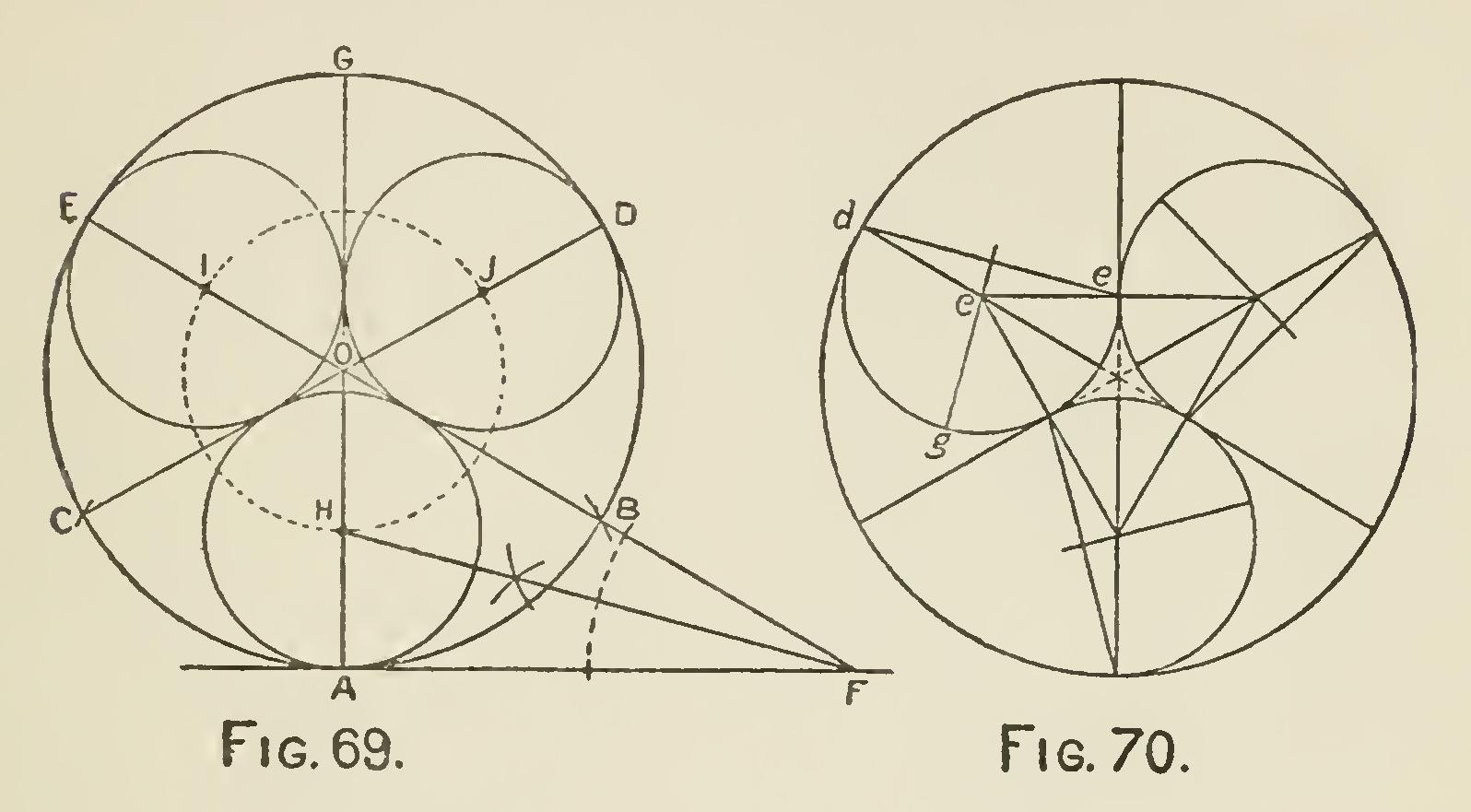
Fig. 69 and 70 are the elementary forms of the tracery shown in Fig. 71.

We show the method of obtaining these curves in Fig. 69 : At any point, as at A, draw a tangent, and A G at right angles to it. From A, with radius 0 A, cut the circle in B and C, and the tangent in the point F, using B as a center.

Bisect the angle 0 at F, and produce the bisecting line until it cuts A G in H. From 0, with radius OH, cut the lines DC and EB in I and J. From H, I and J, with radius HA, draw the three re quired circles, each of which should touch the other two and the outer circle.

After having constructed Fig. 69 we go one step further and form Fig. 70; having inscribed three equal circles in a circle, join their centers, thus forming an equilateral triangle. From the center of the surrounding circle draw radii pass ing through the angles of the triangle and cutting the circle in points; as d and two others. Draw ed and bisect it by cg; then the centers for the curves which are in the semi-circle will be on the three lines, dc, cg and ce.

These curves, in Gothic architecture, are called foliations, or featherings, and the points at which they meet are called cusps. The completion of this study is shown in Fig. 71.

Fig. 72 is the elementary form of the tracery shown in Fig. 73.

Fig. 74 shows the elementary construction of Fig. 75. Draw two diameters (Fig. 74) at right angles to each other, and joint their extremities, thus inscribing a square in the circle. Bisect the quadrants by two diameters cutting the sides of the square in the points as g; join these points, and a second square will be inscribed within the first.

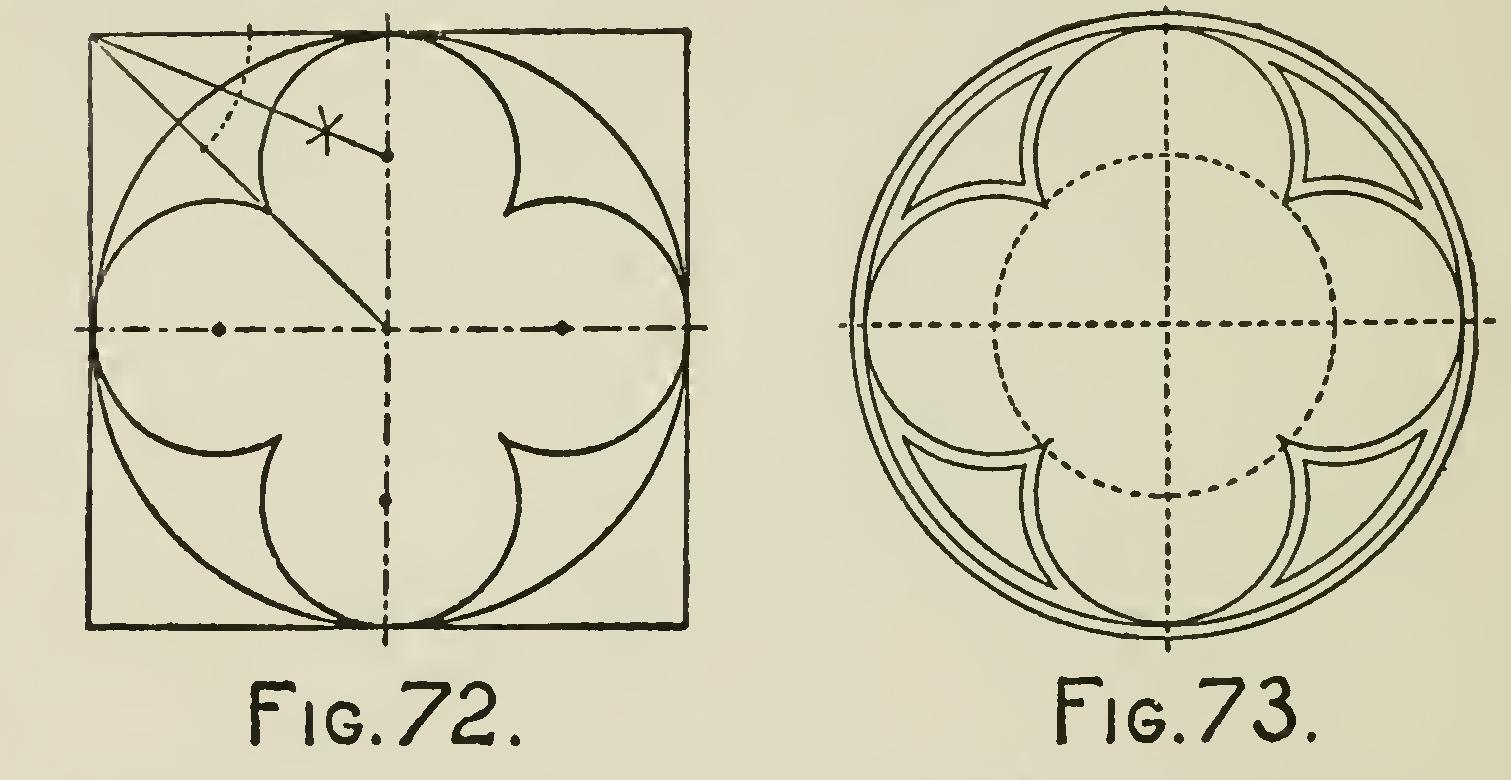
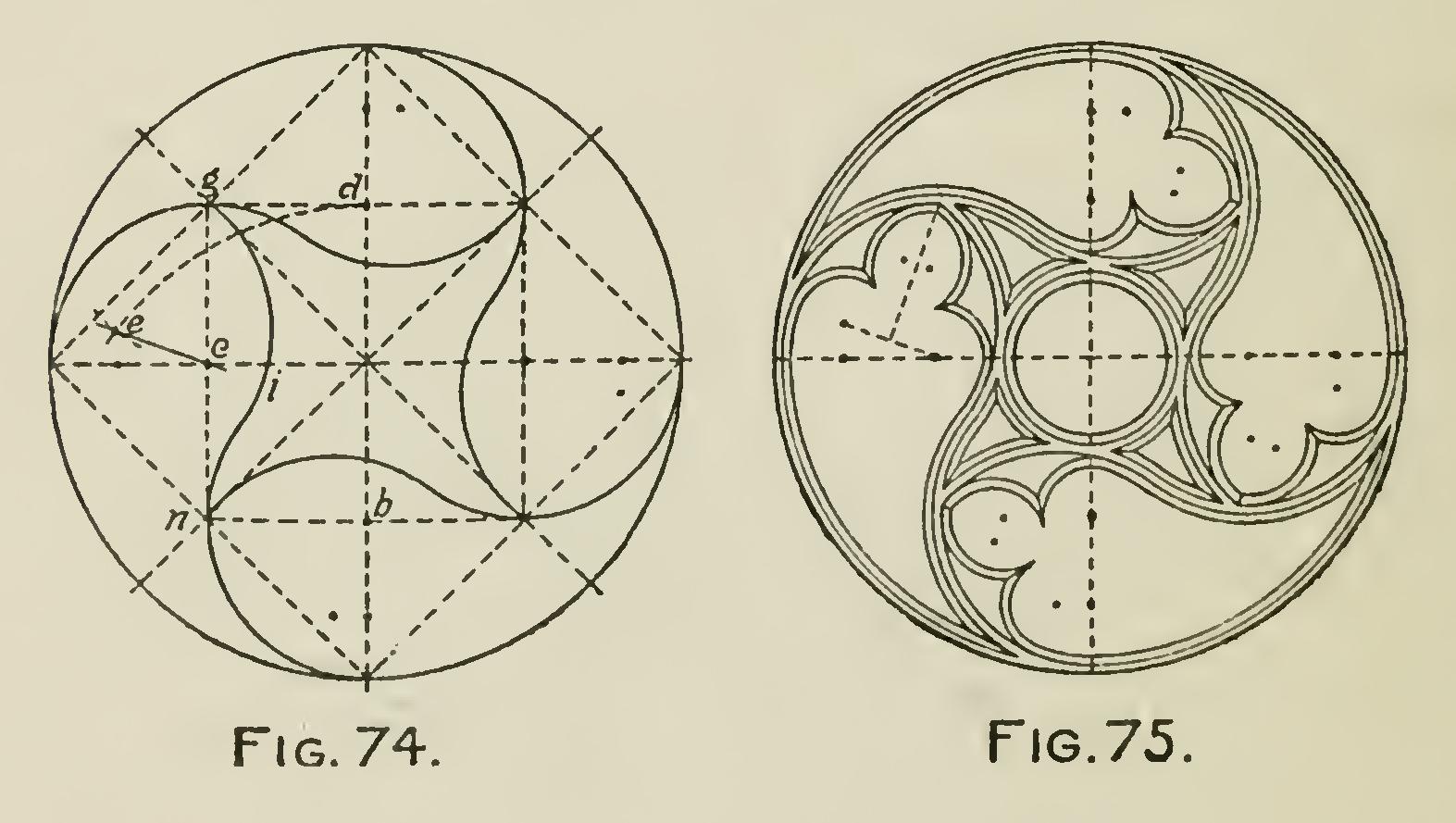
The middle points of the sides of this inner square, as bcd, are the centers of the arcs which start from the extremities of the diameters.

From 13, with radius bd, describe an arc, and from g, with radius gc, describe another cutting the former one in e. Then e is the center for the arc ig, which will meet the arc struck from b, in i. Of course, this process is to be carried on in each of the four lobes.

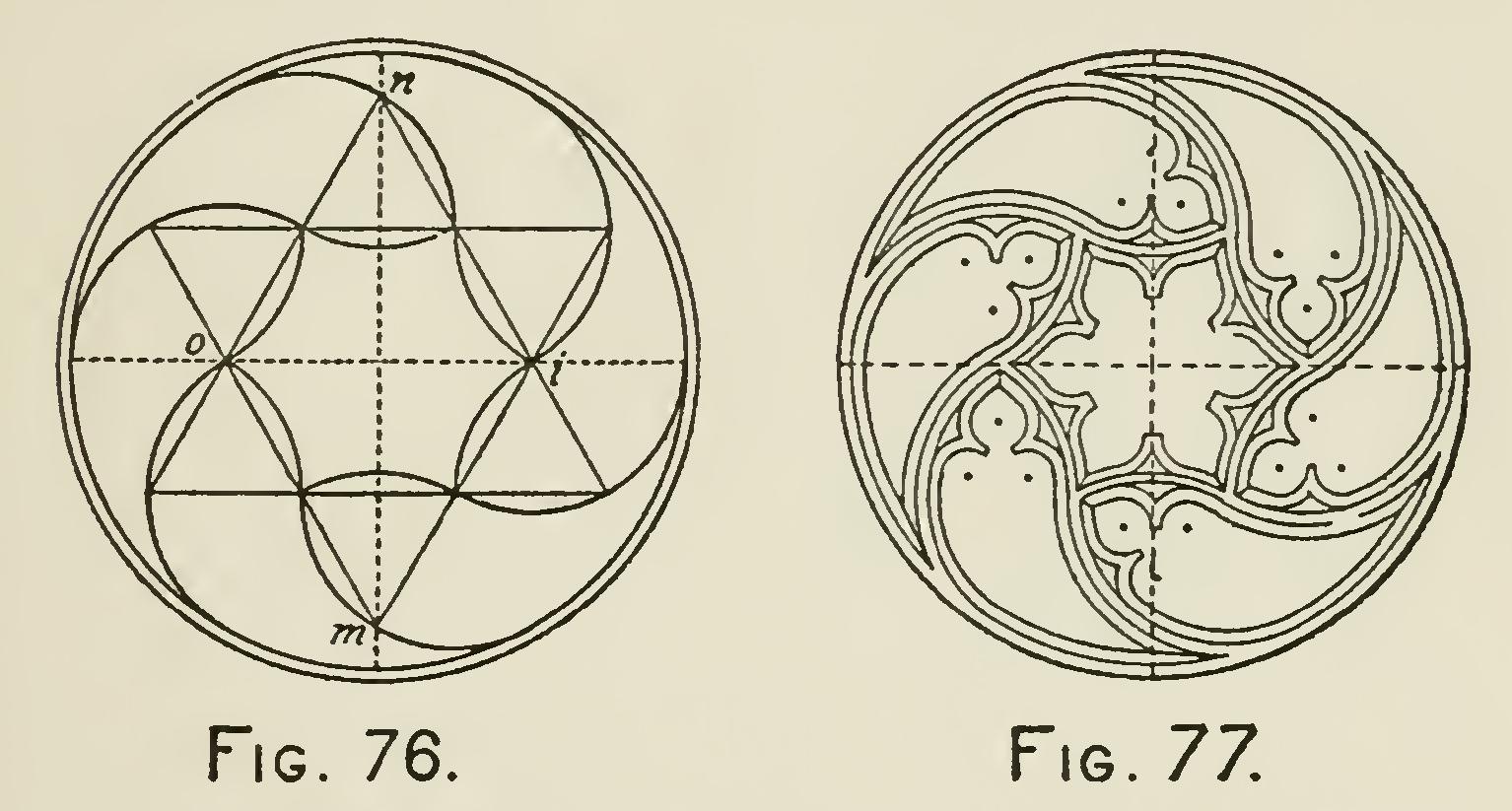
Fig. 75 is the completed figure.

Fig. 76 shows the skeleton lines of Fig. 77. Divide the diameter into four equal parts, and on the middle two, as a common base, construct the two equilateral triangles oin and oim.

Draw lines through the middle points of the sides of the triangles which, intersecting, will complete a six-pointed star in the circle, the angles of which will be the centers for the main lines of the tracery.

Fig. 77 is the completed figure.

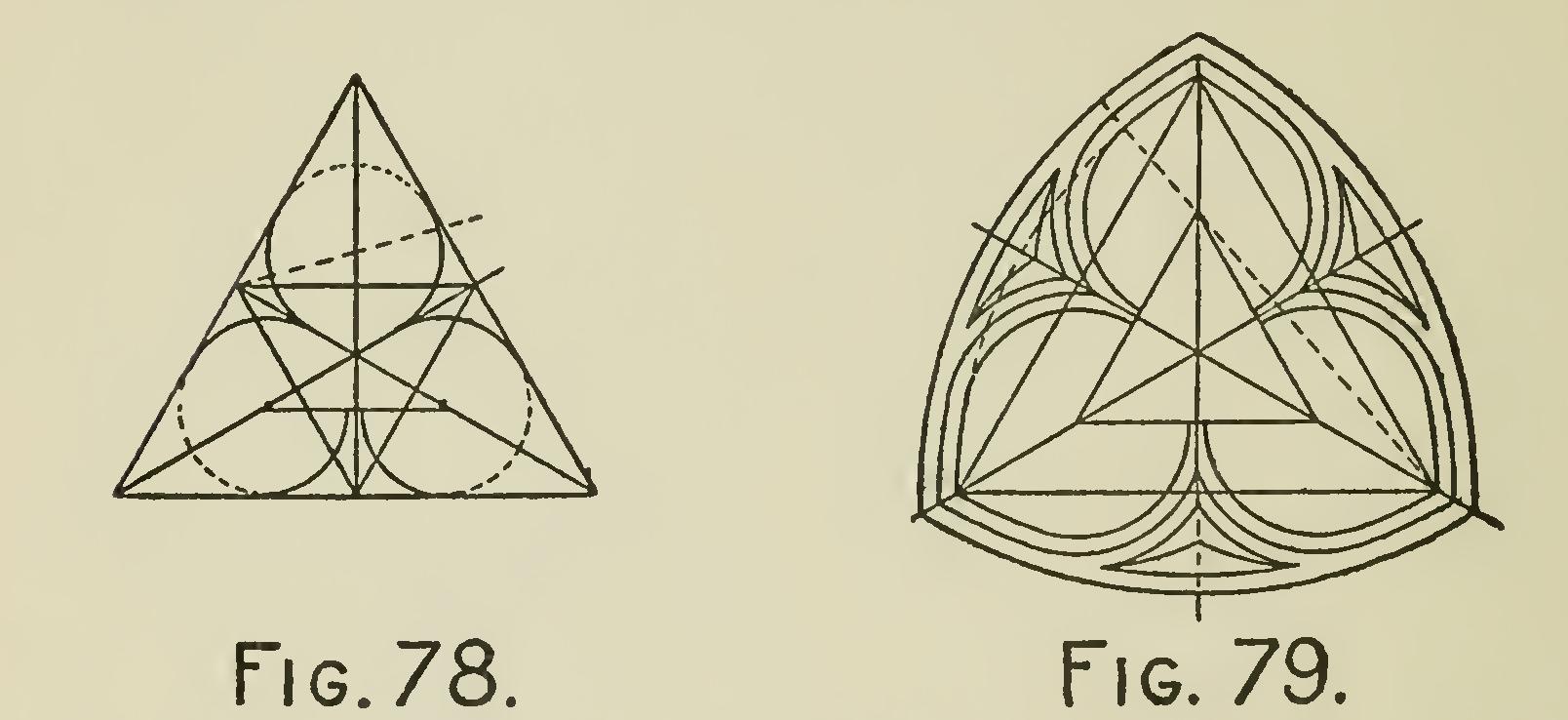
The figures 78 and 79 will be understood with out further instruction than is afforded by the examples.

Fig. SO shows the construction for the tracery in a square panel. From each of the angles of the square (the inner one in this figure), with a radius equal to the length of the side of the square, de scribe arcs; these intersecting will give a four sided curvilinear figure in the center. Draw diagonals in the square.

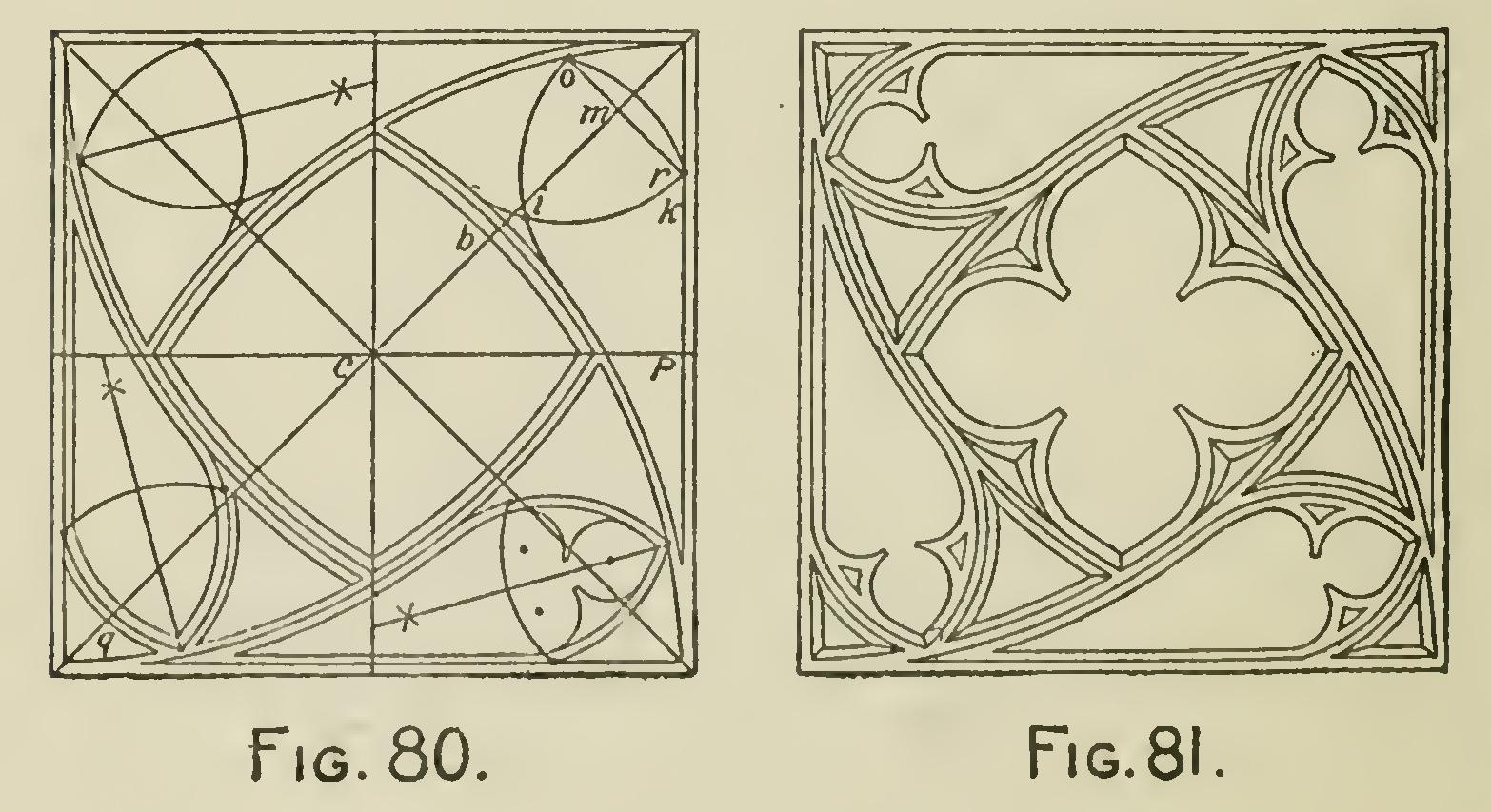
From the point where the diagonal intersects the curve b (the middle line of the three here shown) set off on the diagonal the length cb, viz., bm. From q, with radius mq, describe an arc cutting the original arc in o. Make mr equal to m o.

From o and r, with radius o r, describe arcs intersecting each other in i : produce these until they meet the curve p in n.

The foliation and completion, as shown in Fig. 81, will be found simple.