Method of Shingling

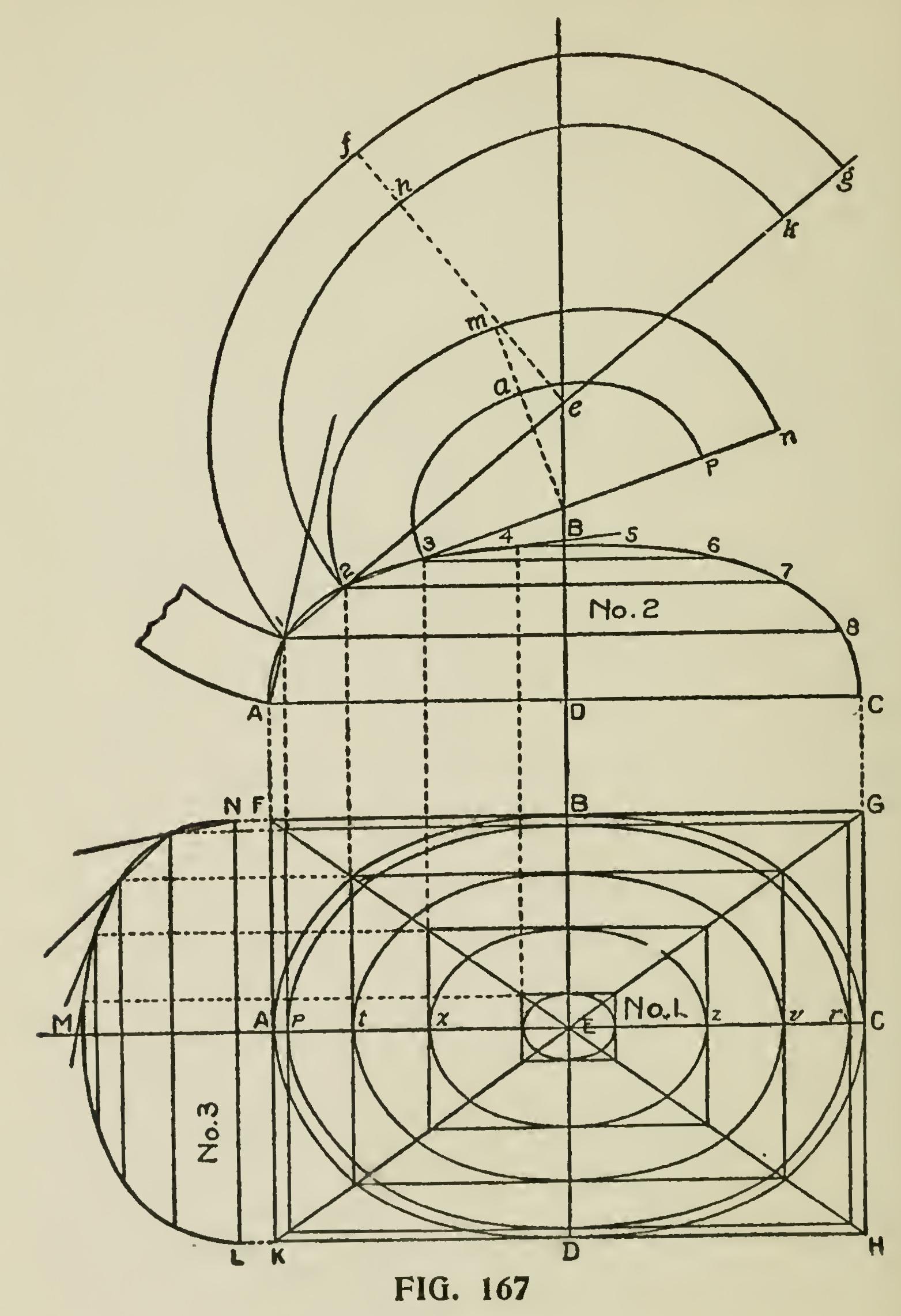
To describe the covering of an ellipsoidal dome with boards of equal width.

Let ABCD (No. 1, Fig. 167) be the plan of the dome, ABC (No. 2) the section on its major axis, and DIN (No. 3) the section on its minor axis. Draw the circumscribing parallelogram of the ellipse FGHK (No. 1), and its diagonals FHGK. In No. 2, divide the circumference into equal parts, 1234, representing the number of covering boards, and through the points of division 18, 27, etc., draw lines parallel to AC. Through the points of division draw 1p, 2t, 3x, etc., perpendicular to AC, cutting the diagonals of the circumscribing parallelogram of the ellipse (No. 1), and meeting its major axis in ptx, etc. Complete the parallel ograms, and their inscribed ellipses corresponding to the lines of the covering, as in the figure. Pro duce the sides of the parallelograms to intersect the circumference of the section of the transverse axis of the ellipse in 1234, and lines drawn through these, parallel to LN, will give the representation of the covering boards in that section. To find

the development of the covering, produce the axis DB, in No. 2, indefinitely. Join by a straight line the divisions 12 in the circumference, and produce the line to meet the axis produced ; and 12ekg will be the axis major of the concentric ellipses of the covering lfg, 2hk. Join also the corresponding divisions in the circumference of the section on the minor axis, and produce the line to meet the axis produced; and the length of this line will be the axis minor of the ellipses of the covering boards.

Before leaving the subject of roofs, it may be as well to remark that the framing of valley roofs is so very much like that of hip-roofs, that it is not necessary to make special drawings for the pur poses of showing how a valley roof is constructed or laid out. The cuts, bevels, lengths and posi tions of rafters and jacks may be easily found if the same principles that govern hip-roofs are followed, as a valley rafter is simply a hip reversed.