Retaining Walls
wall, base, earth, fig, resultant and dam
RETAINING WALLS A wall such as that shown in Fig. 31 is called a retaining wall because its office is to keep a bank of earth in position. The earth to be retained may be that already in place before the wall was built, as where a cut is made in the side of a hill; or the wall may be constructed, and the earth back of it deposited later.
Granular material, such as sand, coal, grain, and such substances, when unsupported on the sides, will assume a conical shape, and the angle made by the slanting side of each cone and the horizontal is peculiar to each substance, and is called the angle of repose of that material. The natural slope or angle of repose of earth is row, the base wide, and a heavy batter on the front.
If failure by overturning were the only thing to consider, a triangular cross-section, as a b c in Fig. 35, would be proper; but a material thick ness at the top must always be provided to with stand shocks, the action of frost, etc. For this reason, a wall sustaining a bank of earth is usually built with a top thickness of at least two feet, and little or no batter on the back. This design makes x large and promotes stability. Where the available space for the base of the wall is limited, as along the edge of a city street, the batter must be on the side toward the bank. In this case, to make x as large as before, the wall must be made thicker.

Stability against Crushing.
Where two forces like W and T in Fig. 36 act at one point, the effect may be combined in one resultant, which takes the place and has the effect of the two. Thus, in Fig. 36, W and T are replaced by their resultant R, which pierces the base at some point to the left of W. This distance (a) de pends upon the relative magnitudes of W and T and the height of T above A B. If a be half of the base, the pressure is evenly distributed over the length A B; but as a becomes smaller, the pressure at A becomes larger, and that at B becomes correspondingly less. It can be provedthat when the resultant is one-third of A B from A, the pressure at A is twice the average pres sure, and that at B becomes zero. At this time the joints on the back of the wall are just upon the point of opening, and, unless the wall is held together otherwise than by gravity, it is in an unstable condition.
In the design of gravity walls, it is an in variable rule to keep the resultant in the middle third of the base. When a is greater than one third of the base, the unit-stress at A is: in which S is the stress per unit of area, and 1 is the length A B or the base of wall.
When a is less than one-third of 1, the stress becomes: When a is just one-third of the base, the results will be the same by either formula. These formulas show that, for a given weight its particles, which it does not long retain. If it is allowed to begin to slide, it is very difficult to hold it with falsework, and the wall must be made heavier than would otherwise be necessary.
In Louisville, Ky., the sliding of a large re taining wall was effectively stopped by erecting a barrier in front of the sliding wall, consisting of another wall of reinforced concrete on piles, and filling in back of same.
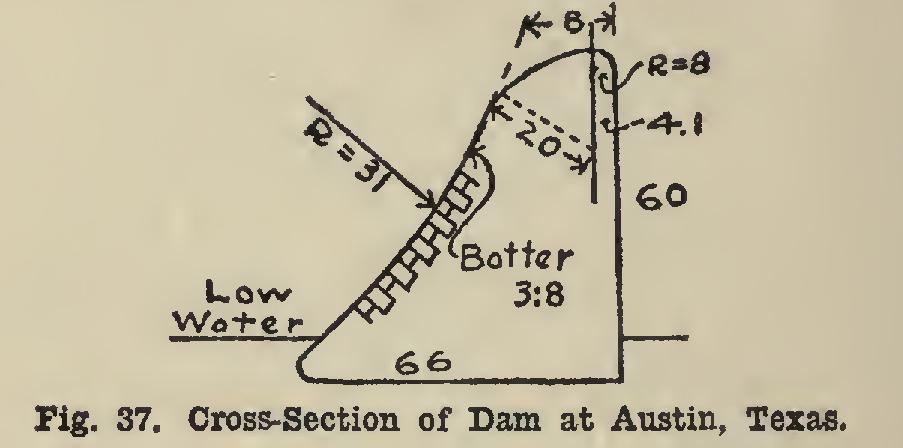
A Dam Failure.
Fig. 37 shows the cross section of a masonry dam on the Colorado river above Austin, Texas, which failed April 7, 1900, letting loose a reservoir of water 30 miles long, half a mile wide, and 50 feet deep. At that time the flood water was so high as to cause a thrust of perhaps 200,000 pounds on each foot of the dam. From the above investigation, it is prob able that this pressure was not enough to cause failure by any of the three ways enumerated. A subsequent investigation showed that the foun dation of the clam had become impaired on the down-stream side, the dam settled and cracked, a part of it was overturned, and part was moved bodily down stream.