Roof Framing

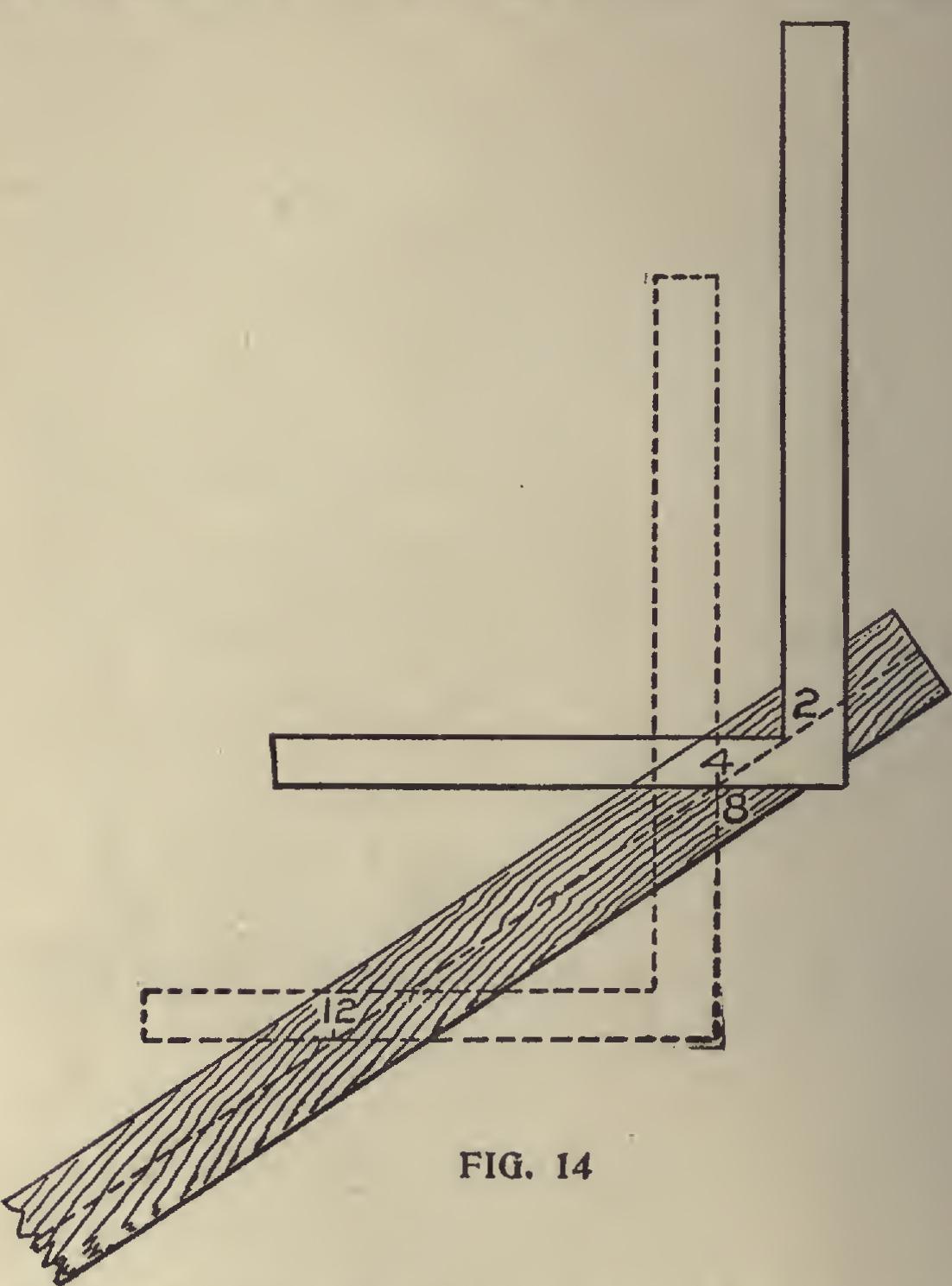
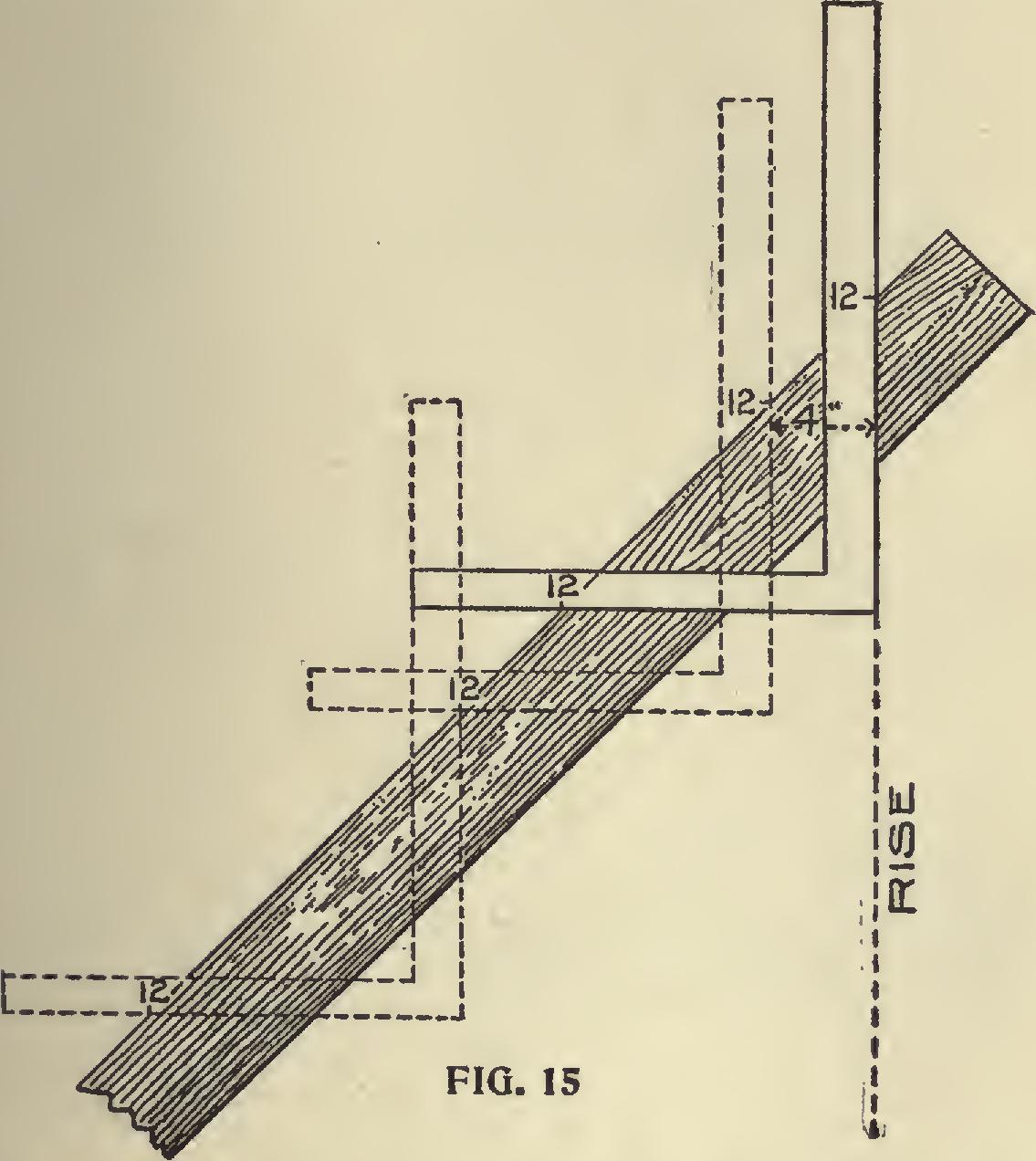
Pitches and Fractions.—Sometimes there may be a fraction of a foot in this division; when such is the case, it can be dealt with as follows: Suppose there is a fraction of a foot in the span, say 8 inches, the half of which would be 4 inches, or one third of a foot; then if the roof is quarter pitch, all to be done is to place the square, with the 4-inch mark on the tongue, and the 2-inch mark on the blade, on the center line of the rafter, and the distance between these points is the extra length required, and the line down the blade is the bevel at the point of the rafter. In Fig. 14, is shown an application of this method, or the correct result may be obtained by measuring at right-angles from the last application of the square as shown in Fig. 15. All other pitches and frac tions can be treated in this manner without over taxing the ingenuity of the workman.

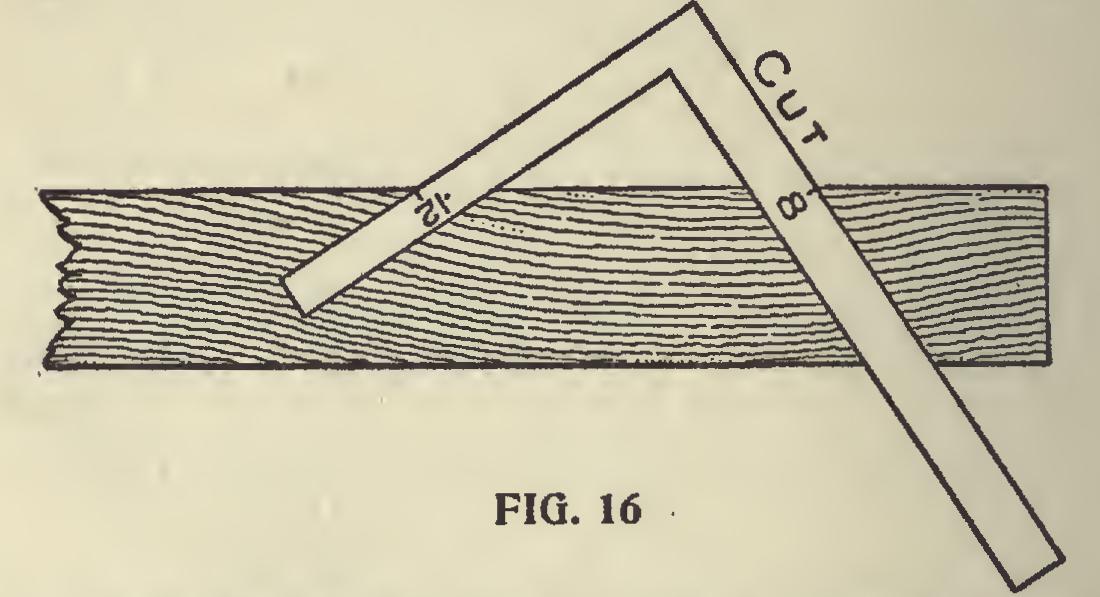
How to Get the Bevels.—Fig. 16 shows how to get the bevels on the top end of vertical board ing, at the gable ends, suitable for the third pitch at Fig. 11.

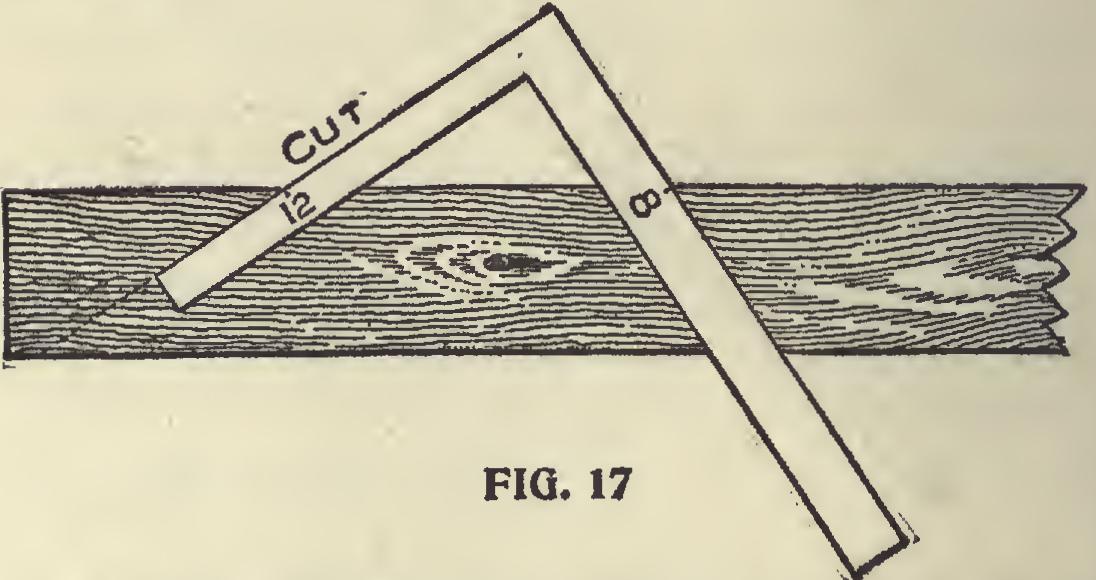
In Fig. 17 is shown a method for finding the bevel for horizontal boarding, collar ties, etc. Both of the above are for the one-third pitch. Roof Pitches Explained.—Inasmuch as roof pitches are not as well understood as they should be, we have thought best at this point to quote from an article, by A. W. Woods, recently pub lished in a trade paper, which will help the student to more fully grasp the subject. In discussing "pitch" he says : The word "pitch" has refer ence to the rise given the common rafter in pro portion to the span. Therefore by letting 12 on the tongue represent the run of the common rafter the figures on the blade will then represent the rise in proportion to its length (the blade), as 6 being one-fourth of 24 represents the quarter pitch, 8 represents the one-third pitch, 12 the one-half pitch, etc. See illustration. Fig. 18. For full illustration of roof pitches see Fig: 49A.

For the corresponding hip or valley for the octagon or square cornered building substitute 13 and 17 on the tongue, respectively. However, neither is absolutely correct, but near enough for practical purposes.

The lengths taken diagonally from 12, 13, and 17 on tongue to the figures designating the rise on the blade represent the lengths of the above rafters for a one-foot run. The diagonal lines in the illustration from those figures to 15 on the blade represent five-eighths pitch. Only three of the lengths out of seventy-two are with out fractions and they are for the common rafters, as follows: 12 to 5=13 inches, 12 to 9=15 inches and 12 to 16=20 inches. It is on the latter that the rule 6, 8, and 10, so generally used for squaring frame work, is founded. Of course, any of the

other angles could be used for this purpose, but the above being without fractions are easy numbers to remember.

The length of the common rafter doubles its run or has a length equal its span when it has a rise of 60 degrees, which taken on the square is 20.784 inches rise to the foot. The same is true of the octagon hip when it has a rise of a fraction less than 23 inches, and that for the common hip at nearly 291 inches rise to the foot.

Reversed Pitches.—In the illustration the re versed pitches are also given, that is by letting the blade represent the run and the tongue the rise. The length of the diagonal lines in that case becomes the length of the rafter for a one foot rise to the inches in run taken on the blade.

The reader will notice that several of these pitches are transposed and are found in the first column, as follows : The 1 pitch is the same as the I pitch when reversed. The same as 1; the same as ; the 1 remains the same or unchanged. The low pitches in the first column become very steep when reversed; thus, the -IA- pitch becomes 6 pitches or a rise of 12 feet to a one-foot run. The pitch is equal to a rise of 6 feet to a 1-foot run, etc.

For the corresponding lengths of the hip or valley for the reversed pitches add one-twelfth and five-twelfths to the run of the common rafter for the octagon and right-angled corner respec tively. In our illustration we also give the degree of pitch for common rafter. To find the same for reversed pitches, it is only necessary to sub tract the degrees here given from 90 degrees.

In the following Mr. Woods gives explanations and diagrams for finding the lengths of rafters where the rises in the roof are of different heights.

Irregular, Uneven, or Unequal Pitches,

are simply different pitches in the same roof. When they are the same on all sides and the building is square, the hips or valleys run in from the corners at an angle of 45 degrees, regardless of the rise of the roof ; but should one side be steeper than the adjoining side, or the gables be of differ ent pitch from the main roof, then the hips or valleys depart from the 45-degree angle.

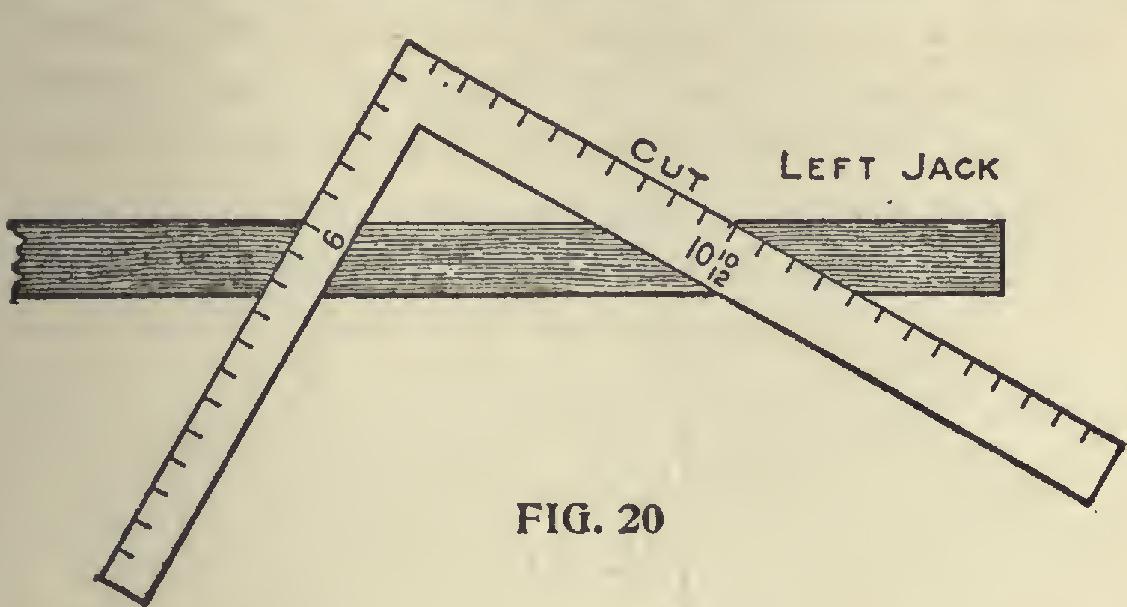
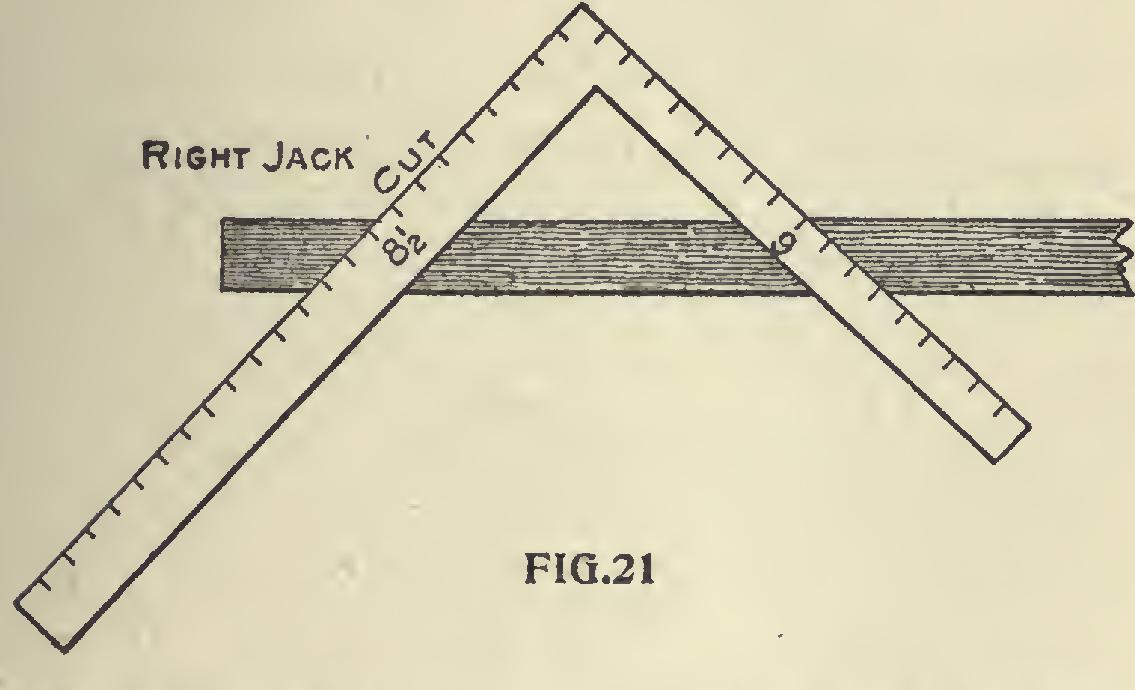
Fig. 19 shows a roof plan with the one-third pitch on the main part, with a half-pitch gable. The seat and down cuts of the jack and common rafters remain the same as in the even pitch roof, except the top cut of the jack.

We will not take up space to explain this cut at length, but will give that obtained by the square as follows: Take to scale the length of the left common rafter on the blade, and the