Geometrical Relations of Cleavage-Forms

GEOMETRICAL RELATIONS OF CLEAVAGE-FORMS The geometrical relations of the cleavage-planes and the relative size and position of the cells vary endlessly in detail, being modified by innumerable mechanical and other conditions, such as the amount and distribution of the inert yolk or deutoplasm, the shape of the ovum as a whole, and the like. Yet all the forms of cleavage are variants of a single type which has been moulded this way or that by special conditions, and which is itself an expression of two general laws of cell-division, first formulated by Sachs in the case of plantcells. These are : I. The cell typically tends to divide into equal parts.

2.

Each new plane of division tends to intersect the preceding plane at a right angle.

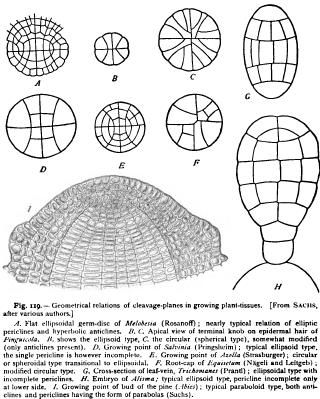
In the simplest and least modified forms the direction of the cleavage-planes, and hence the general configuration of the cellsystem, depends on the general form of the dividing mass ; for, as Sachs has shown, the cleavage-planes tend to be either vertical to the surface (anticlines) or parallel to it (periclines). Ideal schemes of division may thus be constructed for various geometrical figures. In a flat circular disc, for example, the anticlinal planes pass through the radii ; the periclines are circles concentric with the periphery. If the disc be elongated to form an ellipse, the periclines also become ellipses, while the anticlines are converted into hyperbolas confocal with the periclines. If it have the form of a parabola, the periclines and anticlines form two systems of confocal parabolas intersecting at right angles. All these schemes are, mutandis, directly convertible into the corresponding solid forms in three dimensions. Sachs has shown in the most beautiful manner that all the above ideal types arc closely approximated in nature, and Rauber has applied the same principle to the cleavage of animal cells. The discoid or spheroid form is more or less nearly realized in the thalloid growths of various lower plants, in the embryos of flowering plants, and elsewhere (Fig. 119). The paraboloid form is according to Sachs characteristic of the growing points of many higher plants; and here too the actual form is remarkably similar to the ideal scheme (Fig. 119, I).

For our purpose the most important form is the sphere, which is the typical shape of the egg-cell; and all forms of cleavage are derivatives of the typical division of a sphere in accordance with Sachs's laws. The ideal form of cleavage would here be a succession of

rectangular cleavages in the three dimensions of space, the anticlines passing through the centre so as to split the egg in the initial stages successively into halves, quadrants, and octants, the periclines being parallel to the surface so as to separate the inner ends of these cells from the outer. No case is known in which this order is accurately followed throughout, and the periclinal cleavages are of comparatively rare occurrence, being found as a regular feature of the early cleavage only in those cases where the primary germ-layers arc separated by delamination. The simplest and most typical form of eggcleavage occurs in eggs like those of echinoderms, which are of spherical form, and in which the deutoplasm is small in amount and equally distributed through its substance. Such a cleavage is beautifully displayed in the egg of the holothurian Synapta, as shown in the diagrams, Fig. 120, constructed from Selenka's drawings.' The first cleavage is vertical, or meridional, passing through the egg-axis and dividing the egg into equal halves. The second, which is also meridional, cuts the first plane at right angles and divides the egg into quadrants. The third is horizontal, or equatorial, dividing the egg into equal octants. The order of division is thus far exactly that demanded by Sachs's law and agrees precisely with the cleavage of various kinds of spherical plant-cells. The later cleavages depart from the ideal type in the absence of periclinal divisions, the embryo becoming hollow, and its wall consisting of a single layer of cells in which anticlinal cleavages occur in regular rectangular succession. The fourth cleavage is again meridional, giving two tiers of eight cells each ; the fifth is horizontal, dividing each tier into an upper and a lower layer. The regular alternation is continued up to the ninth division (giving 512 cells), when the divisions pause while the gastrulation begins. In later stages the regularity is lost.