Pictorial Drawing 110

The next point d, together with the sym metrical point on the left side of the arch, is at a distance from the center line equal to 1-2. This distance is in the plane of o'z', and so will be laid off in its true length at 1'-2'. Next, the point d is at the perpendicular distance 2h-dh from the vertical plane of ohzh, and this distance will appear as the 45-degree .line through 2', locating a point m' on the base line of the front face of the arch. The point d' is then found in a vertical line through m' at a height equal to mvdr.

Next in turn, e' is located by the vertical line through d'; and f' found by the co-ordinates 1h-3", 3"-nh, and nv-f'.

The rest of the corners are located similarly.

Since parallel lines must show parallel in oblique projection, the lines p'-r', e'-f', s'-t', c'-d', u'-x', and a'-z' should all be parallel. The long edges of the stones are drawn back at 45 degrees, their lengths being taken directly from the plan.

As the back end of the arch is in a plane per pendicular to the length, it follows that if it were all drawn in, it would be of the exact size and shape of the given elevation.

In fact, a more direct method of construction for the oblique view would be to construct the back end first, true size and shape; then, from each point, draw lines forward at 45 degrees, with lengths equal to the lengths in plan. This short construction, of course, would not be ap plicable if the back face had any other direction.

131. The reader should work out the follow ing exercises for himself.

Exercises for Practice (a) Draw an isometric view of a circular cylinder 2 inches in diameter and 4 inches long, placed with the axis horizontal. Show the ele

ments of the cylinder running backward and to the right. Show a square hole inch in diameter cut through the center of the cylinder from end to end.

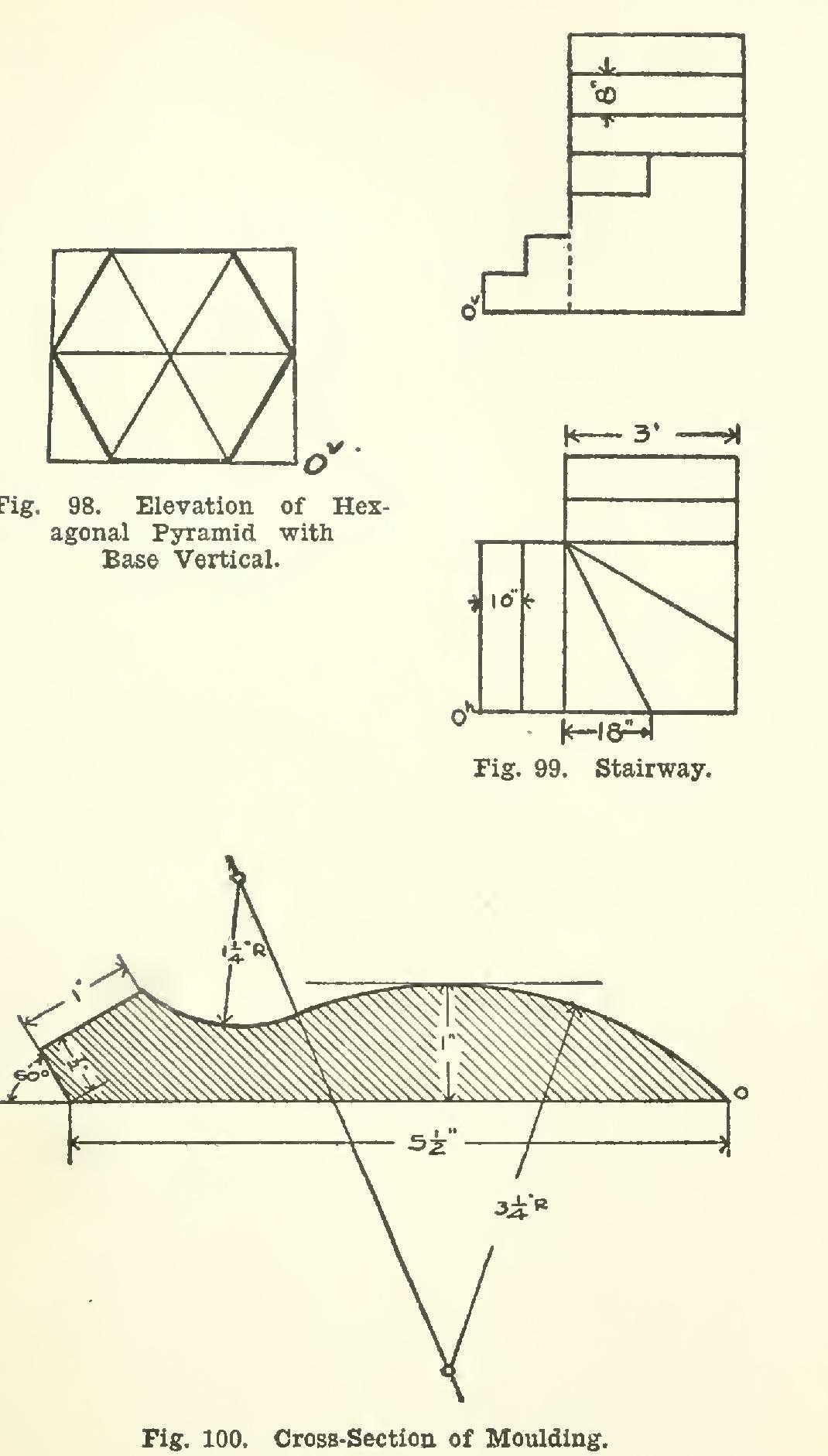
(b) Draw the isometric of a regular hex agonal pyramid when the base is in a vertical plane. Take for the lowest corner of the isometric, point 0 as indicated in the elevation, Fig. 98. Make each edge of the base inches long, and the altitude of the pyramid 4 inches.

(c) Make the isometric of the stairs shown in Fig. 99, taking 0 as the lowest corner of the isometric. Scale, in.=1 ft.

(d) Make the isometric of the moulding shown in cross-section in Fig. 100, taking 0 as the lowest corner. Make the length of the moulding 8 inches. This may be drawn half size, if desired. Before drawing the isometric, the section must be drawn from the given directions.

(e) Draw in oblique projection a right cir cular cone standing on its base. The diameter of the base is 2 inches, and altitude is 4 inches.

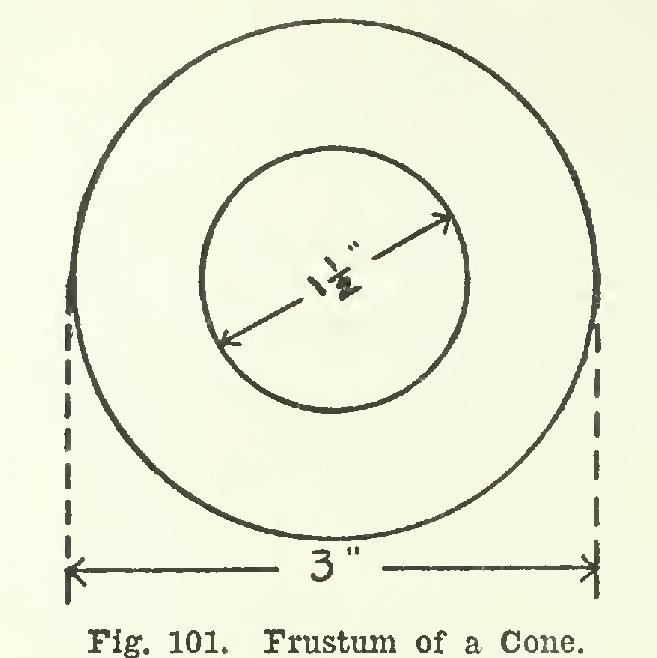
(f) Make the oblique projection of the frustum of a cone, which is shown in elevation in Fig. 101. The axis of the frustum is inches long.

(g) Draw the oblique projection of a wooden box, of which an end view is shown in Fig. 102. The length is 12 inches. The box, including the cover, is made of stock, with the ends nailed onto the sides, and the bot tom nailed to the ends and sides. Make the drawing one-quarter size.

(h) Draw in oblique projection the metal bathtub shown in Fig. 103, disregarding the thickness of the metal. Show the length hori zontal, and the width at 45 degrees: Scale 1 inch=1 ft.