Projection 49

60. Direction of Oblique Lines; Slope. A line may be parallel to one plane and oblique to the other, or it may be oblique to both planes. This latter position will be meant when a line is referred to simply as an oblique line. The term slope refers to the direction of a line oblique to one or both of the co-ordinate planes. In this treatise the word backward, when applied to the slope of a line, means away from the draftsman; and forward means toward the draftsman.

Thus, if a line is said to slope upward, back ward, and to the left, the upper end of the line must be away from the draftsman and toward his left. In the same manner, a line sloping downward, backward, and to the right, has its lower end away from the draftsman and toward his right. If a line slopes simply forward and to the left, for example, then neither end is lower than the other, and the line is in a hori zontal position, with its left-hand end toward the draftsman.

As illustrations of slope of lines, a-1 in Fig. 48 slopes downward and toward the left; a-4, downward and toward the right; a-2, down ward, backward, and toward the left; a-6, down ward, forward, and toward the left; a-3, downward, backward, and toward the right; and a-5, downward, forward, and to the right.

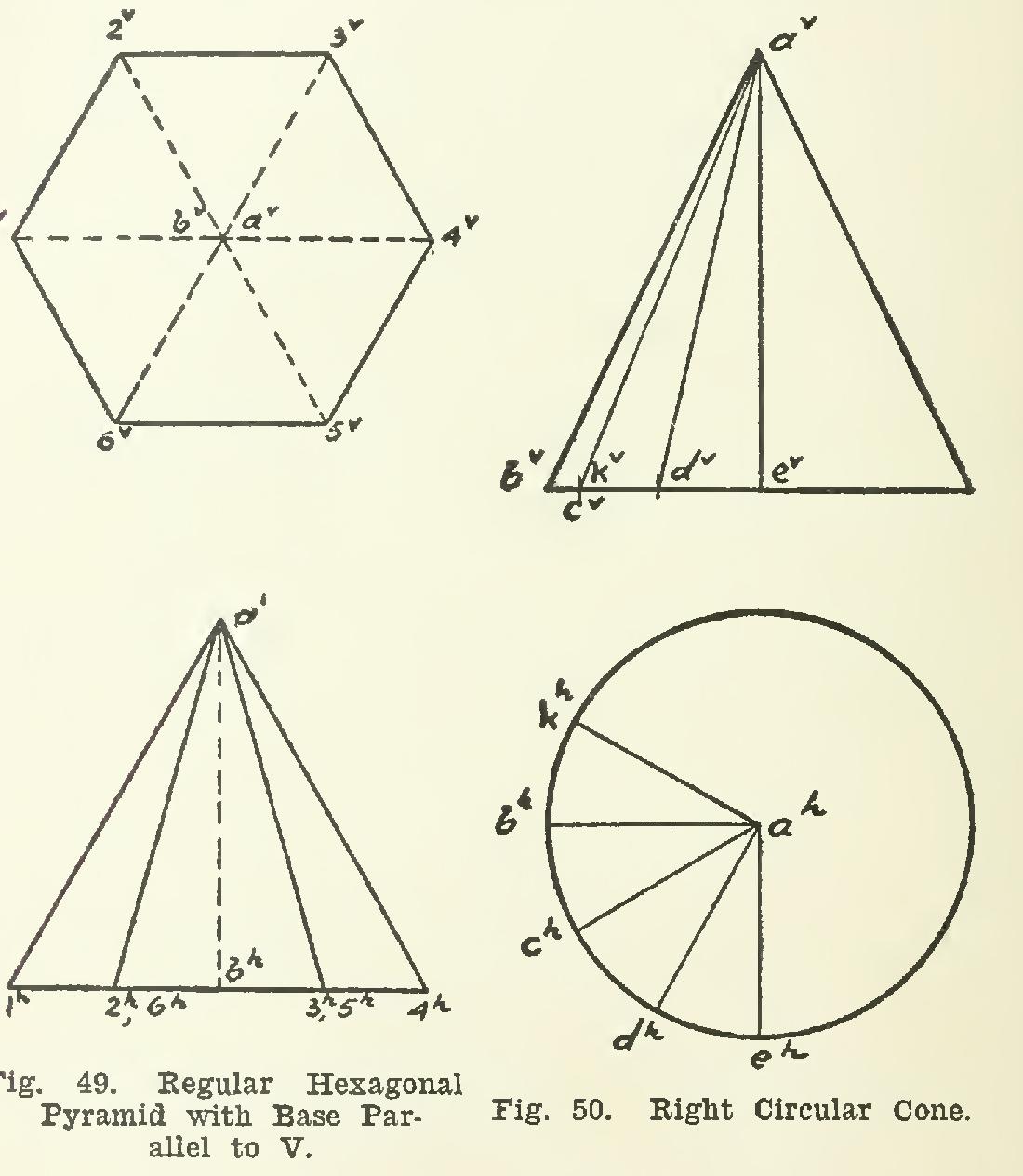
61. Projection of Oblique Lines. A right circular cone is shown in Fig. 50. The vertex is a; and a-b, a-c, a-d, a-e, and a-k are various elements of the cone. On reflection, it will be seen that all of these lines have the same actual length in space. These lines are also all equally inclined to the horizontal plane, and therefore the H projections are all of the same length. Next, referring to the elevation, a°-b° shows the actual length of a-b; a°-c°, a°-d°, and av-e° show gradually decreasing lengths, a°-e° being the shortest of all.

This difference in length corresponds to the fact shown in the plan, that a-e makes the greatest angle with the V plane. That is, the greater the angle that a line makes with a plane of projection, the less will be the length of its projection on that plane.

Observe also that ah-ch and ah-kh make the same angle with V; therefore the lines in space must make equal angles with V; and their V projections, being coincident, are of the same length. Hence lines of equal length which have the same inclination with V, are projected on V in equal lengths.

From the above, it follows that, for a line of definite length, the length of its projection on any plane is determined wholly by the angle the line makes with the plane. If the line makes

the greatest possible angle with the plane (90 degrees), then the projection on the plane has no length, but is simply a point.

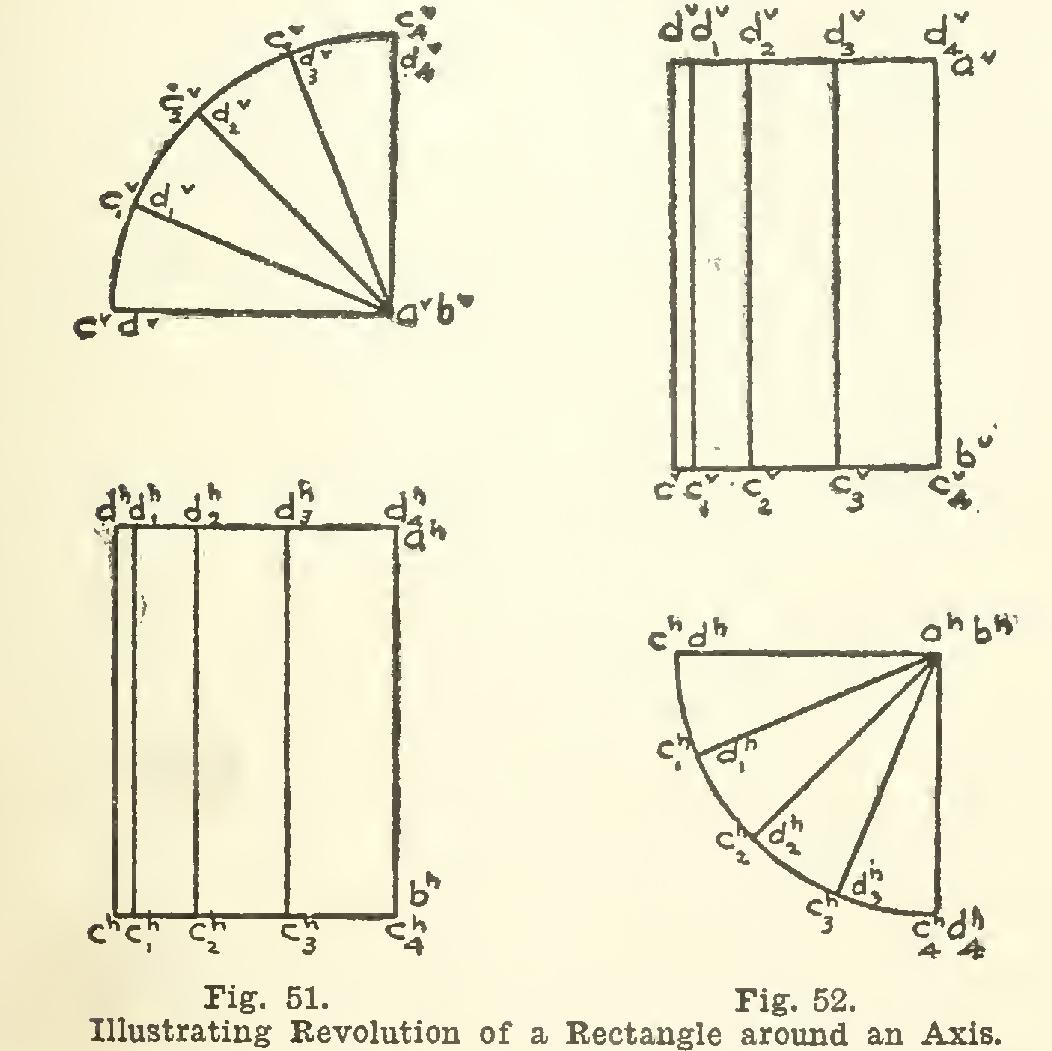
62. Revolution of a Figure around Some Line as an Axis. In Fig. 51, consider first the rectangle abed, placed horizontally, and having its long edges perpendicular to V. Then ebbed' is the true size and shape of the figure. The rectangle is perpendicular to V, and therefore (Article 58) is shown on V as a single line aye. Now let the rectangle revolve up like a trap door, on ahbh as an axis. Then points d and e will revolve in arcs of circles having points a and b respectively as centers. These circles will be perpendicular to the axis ab, and hence parallel to V, so that a circle drawn on V, with center at a'', and with radius a°-c°, will be the projection of the circles de scribed by points c and d in space.

As the rectangle turns about axis a-b, it remains always perpendicular to V, and its pro jection on V will remain a straight line. Then, when the rectangle has swung up through 45 degrees, for instance, its V projection will be a line making 45 degrees with the horizontal; and its plan or H projection, show ing less than the real width, will be The other oblique positions are found in the same way—the elevation first, then the plan. Finally, when the rectangle is revolved through 90 degrees into a vertical position, the H pro jection becomes merely the one line In Fig. 52, the rectangle abed is placed in a vertical position and parallel to V. It is then revolved like a door on its hinges about a-b as an axis, the successive positions appearing in plan at a etc., until the sup posed door is wide open in the position The corresponding elevations etc., are then constructed by projecting directly from the plan.

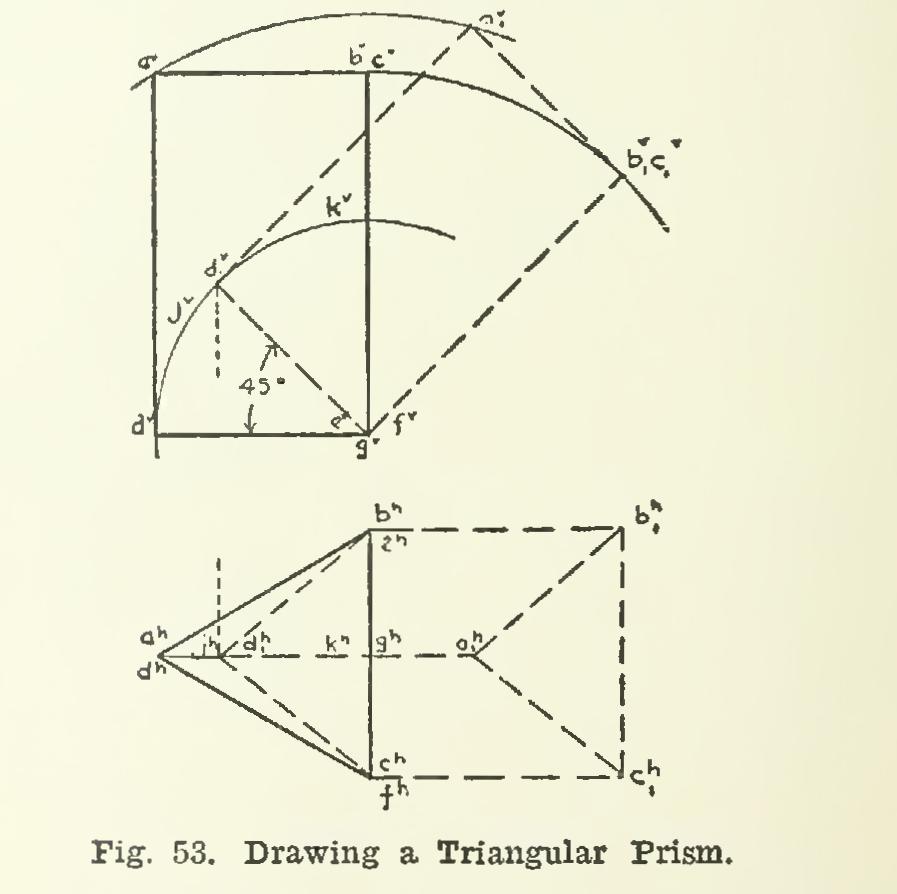
63. Suppose that it is required to draw a tri angular prism standing on one end, and with one edge of the base at right angles with the V plane, Fig. 53. According to the preceding directions, the base is drawn first, placed in a horizontal position, and with the right-hand side perpendicular to V. The elevation may then be drawn as before explained.