Key to Steel Square

To Find the Common Difference in the Length of Jacks multiply the length of the common rafter (14.42) by the number of inches in the spacing, and divide by 12. Thus, if the jacks be placed 16 inches on centers, 14.42x16=230.72; divide by 12=19 and two-twelfths inches.

To Find the Common Difference for the Octagon Jack multiply 14.42 by 2.4, and the product by the spacing, and divide by 12. Thus : 14.42 x2.4= 34.608 x 16=553.728 divide by 12=46 and one twelfth inches.

For the Side Cut of the Jack.

Take 12 on the tongue and 14.42 (14 and five-twelfths) on the blade. The blade will give the desired cut.

For the Side Cut of the Octagon Jack.—Take 5 on the tongue (because 5 is practically equal to the side of an octagon when the diameter is one foot) and 14 and five-twelfths on the blade, the blade giving the cut.

The figures that give the side cut of the jacks in either of the above cases will also give the cut across the face of the roof boards to fit in the valley or over the hip. The tongue gives the cut.

For the Side Cut of the Hip or Valley.

Take 17 on the tongue and 18.79 (18 and 19-24) on the blade, the blade giving the cut. Backing of the hip. Take 8 on the tongue and 18.79 on the blade. The tongue will give the required bevel. A quicker way, however, is to set off the thick ness of the hip along the line of the seat cut (or a line parallel with it), which will give the gauge point from which to remove the wood to the center of the back of the hip. The backing for the octagon hip is practically one-half of that for a hip resting on a square corner.

Table of Tangents.

Fig. 114a represents the table of tangents.

The figures in the two circles represent the degree. Those in the inner circle represent the tangents, and those in the outer represent the co-tangents, the sum of the two always equaling 90 degrees.

The set number is in either case 12 on the tongue and tangents on the blade. The blade gives the cut up to 45 degrees, then it reverses to the tongue from 45 degrees to 90 degrees.

Example: To Frame a Roof With

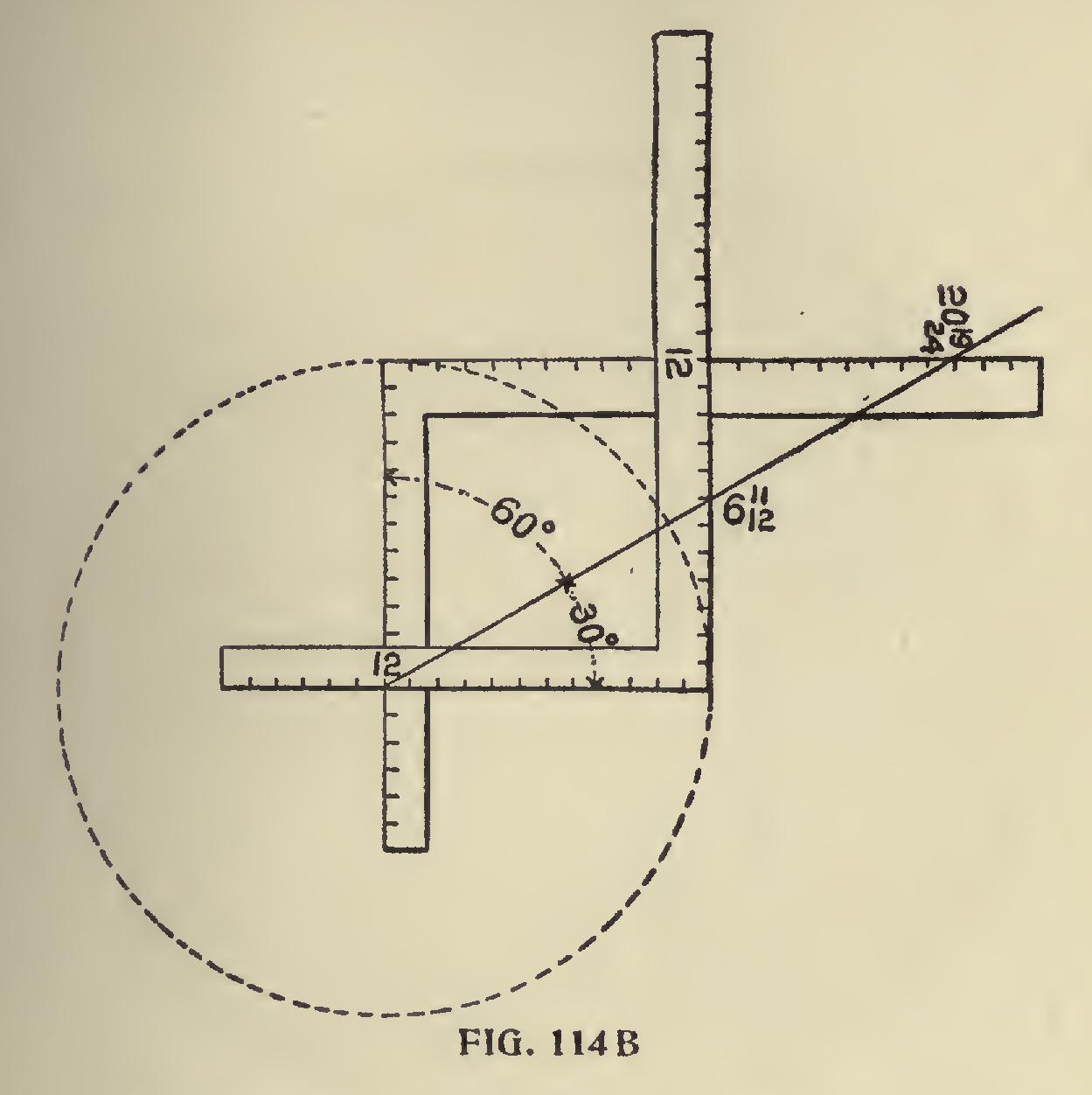
30 Degrees Pitch.—Operations: Turn the slot till it rests opposite 30 degrees and you have, as shown in Fig. 114b: Common Rafter.—Take 12 on the tongue and 6.93 (6 and 11-12) on the blade.

Octagon Hip.

Take 13 on the tongue and 6 and 11-12 on the blade.

Hip or Valley.

Take 17 on the tongue and 6 and 11-12 on the blade. The tongue in either of the above cases gives the seat cut and the blade the plumb cut.

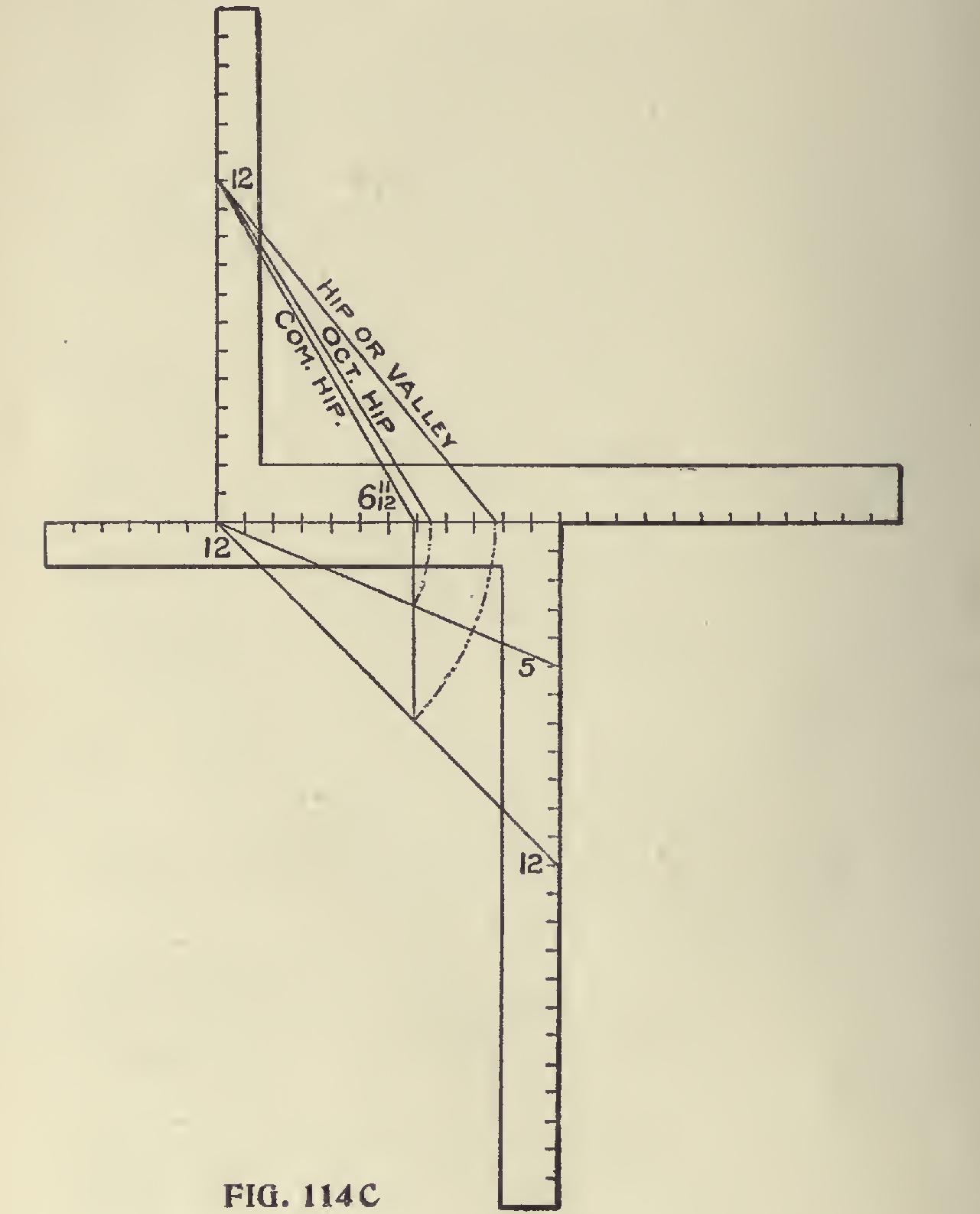
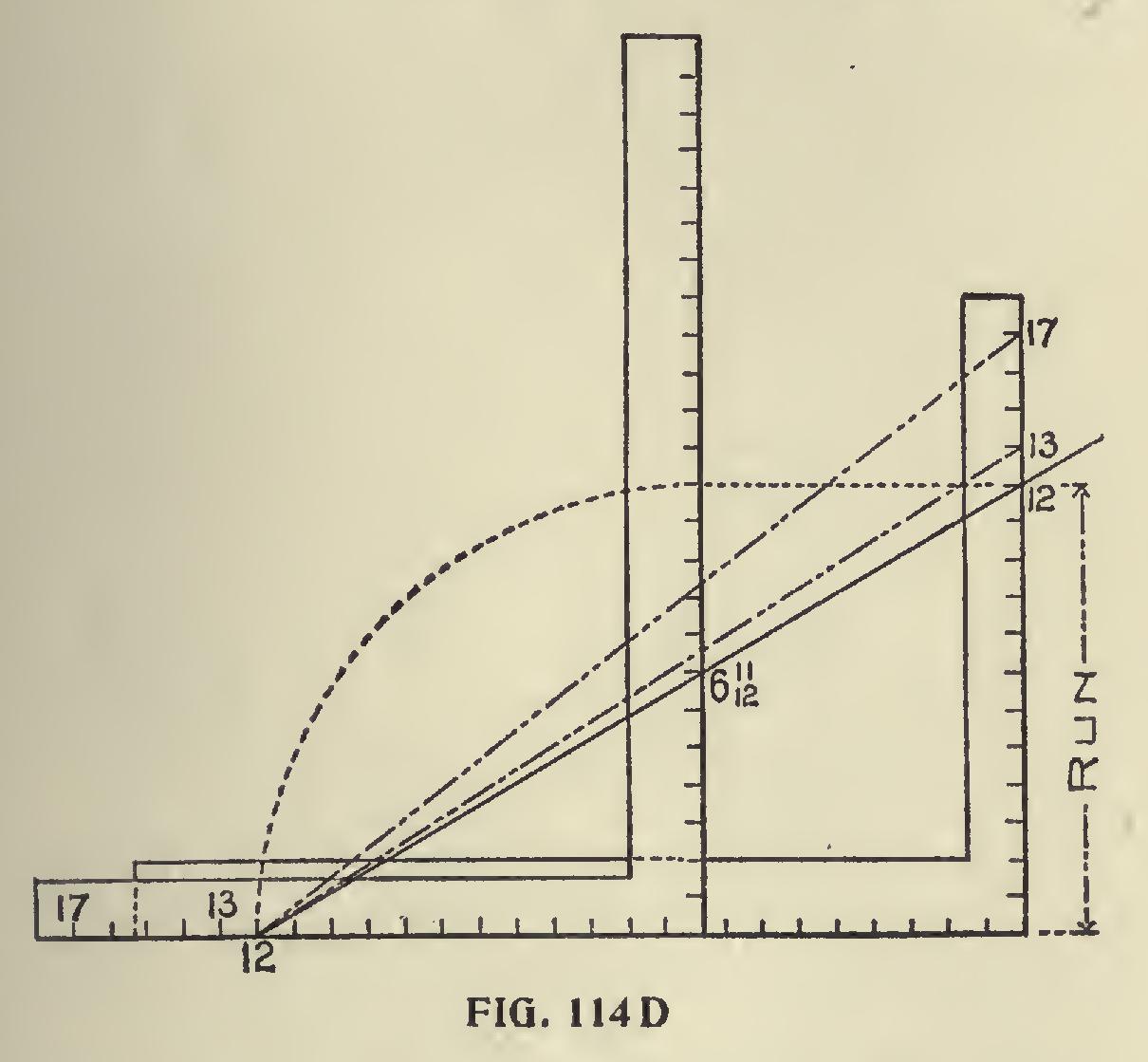
Side Cut of Jack.—Take 12 on the tongue and the diagonal length from 12 to 6 and 11-12 taken on the blade. The blade will give the cut. Side cut of octagon jack. Take 5 on the tongue and proceed as for the common jack Side Cut of Flip or Valley.—Take 17 on the tongue and the length from 17 to 6 and 11-12 taken on the blade. The blade will give the cut. If the roof be 60 degrees pitch proceed the same as for the 30 degrees pitch (using the same figures), but the cuts are reversed on the square. However, this only applies to the seat and plumb cuts of the common rafter. The same may be obtained for the hips, as shown in Fig. 114c, but the lengths of the rafters are not so readily obtained as before because what was the run is now the rise. To get the lengths by scale it is necessary to extend the pitch lines till the base or run of the common rafter equals 12 inches, as shown in Fig. 114d.

To Find the Miter for Any Regular Polygon.— Divide 180 by the number of sides in the polygon.

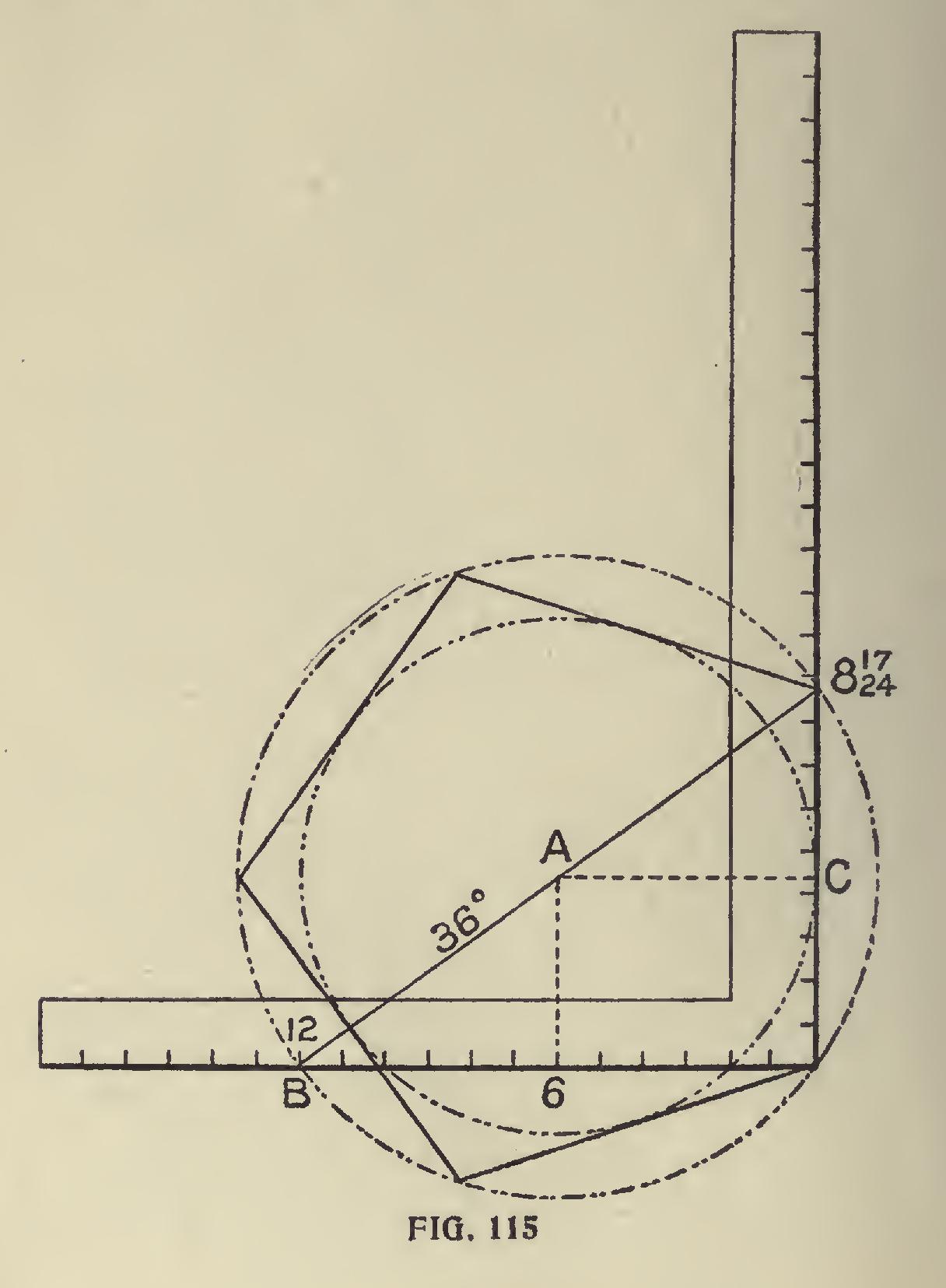
The quotient will be the degree of the miter. Example : Find the miter for a pentagon. 180 degrees divided by 5=36 degrees. Turn the slot to 36 degrees and we have 8.72 (8 and twenty-fourths). Take 12 on the tongue and 8 and 17-24 on the blade, the blade giving the miter. The figures on the blade also give the length of the sides of the pentagon when the inscribed diameter is one foot. By squaring up from 6 on the tongue as shown will locate the center at A. A-C is the radius for the inscribed diameter, and A-B the same for the circum scribed diameter.

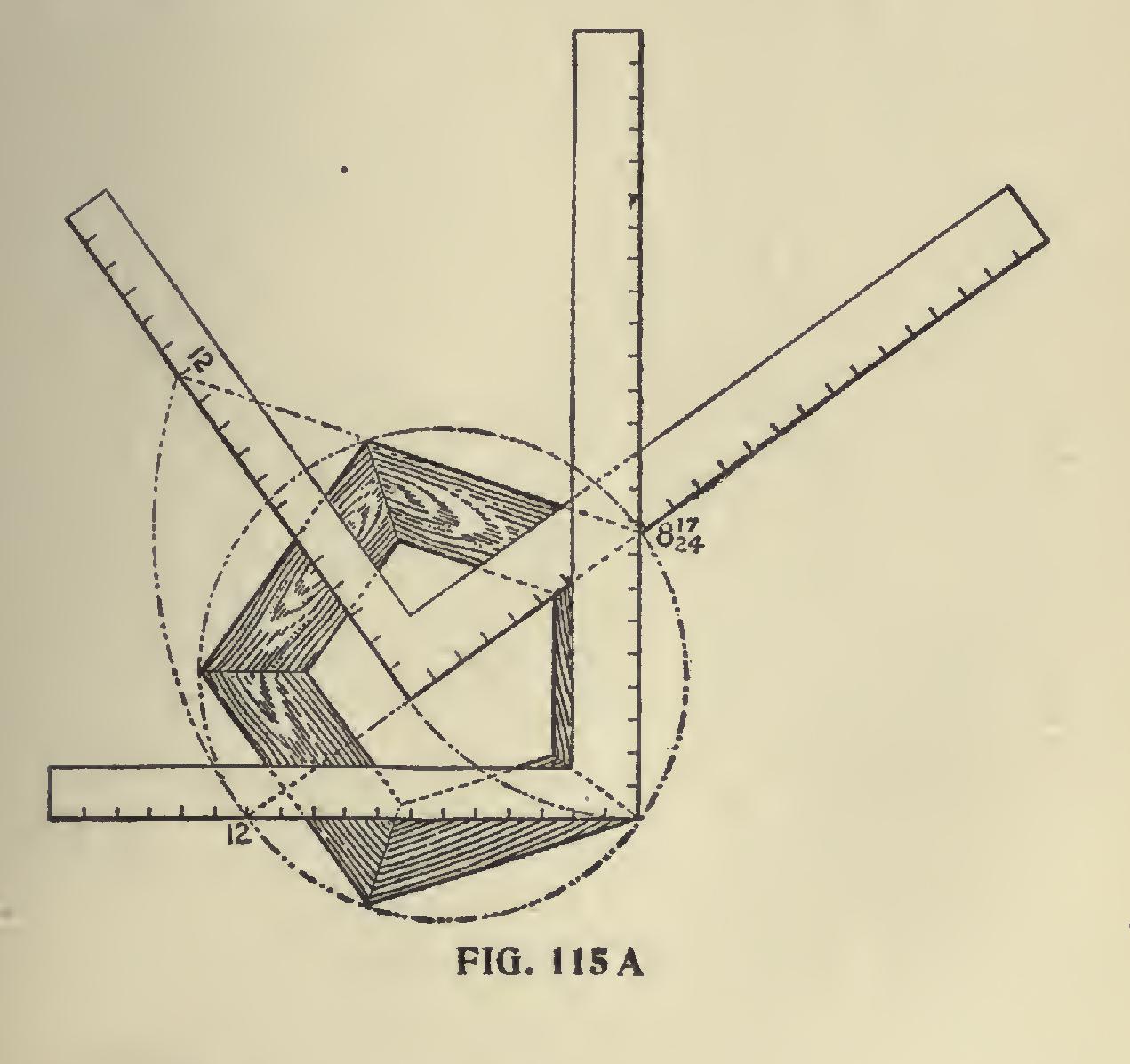
If we let 8 and 17-24 act as a pivot as shown in Fig. 115 and swing the blade till it rests along the 36 degree line, it will show as in Fig. 115a. The 12 on the tongue will rest in line with one of the sides of the pentagon and the blade will rest along the line of the miter, thus proving that the latter gives the cut. The figures 8 and 17-24 also represent the length of one of the sides when the inscribed diameter is one foot.