Key to Steel Square

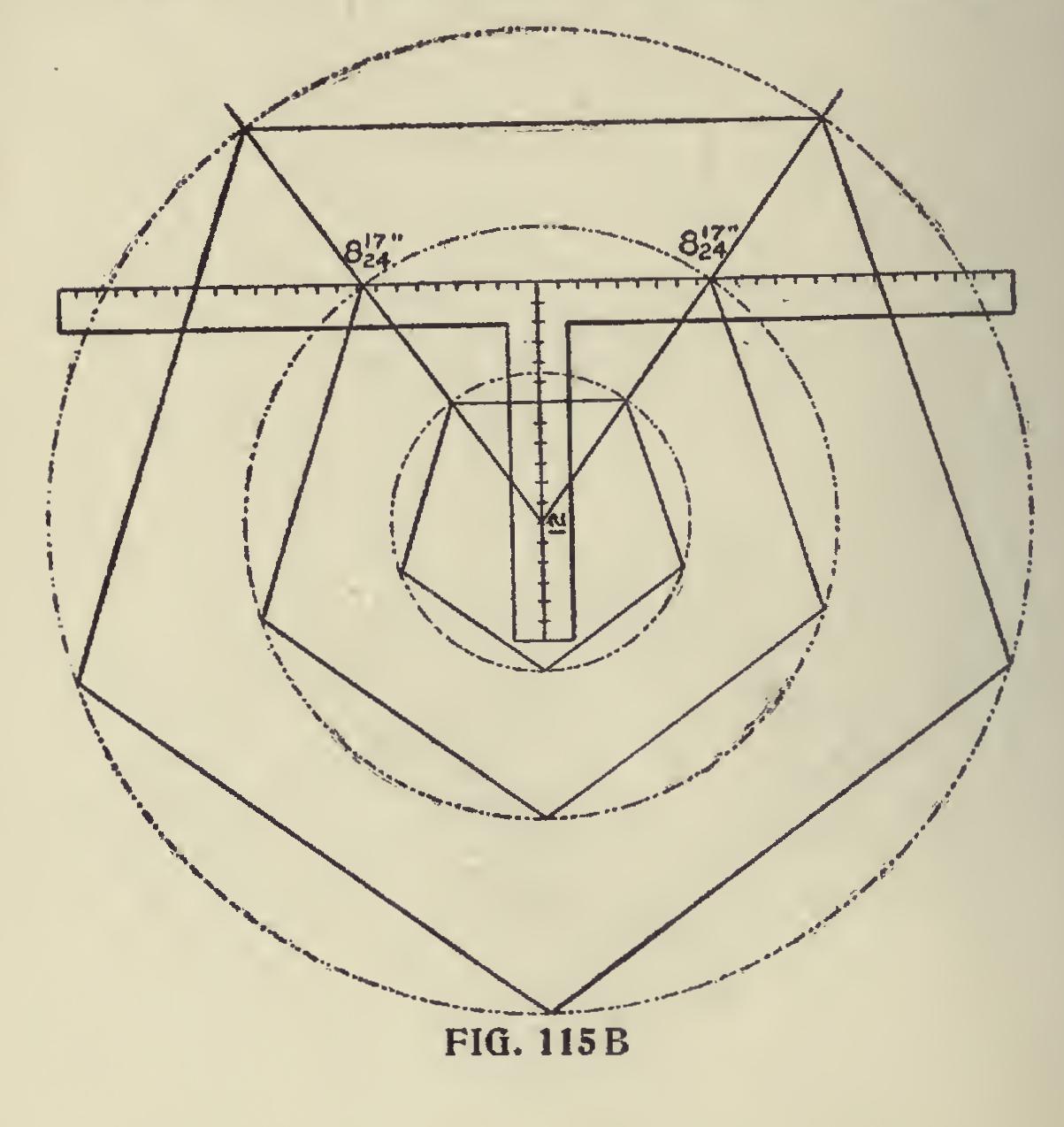
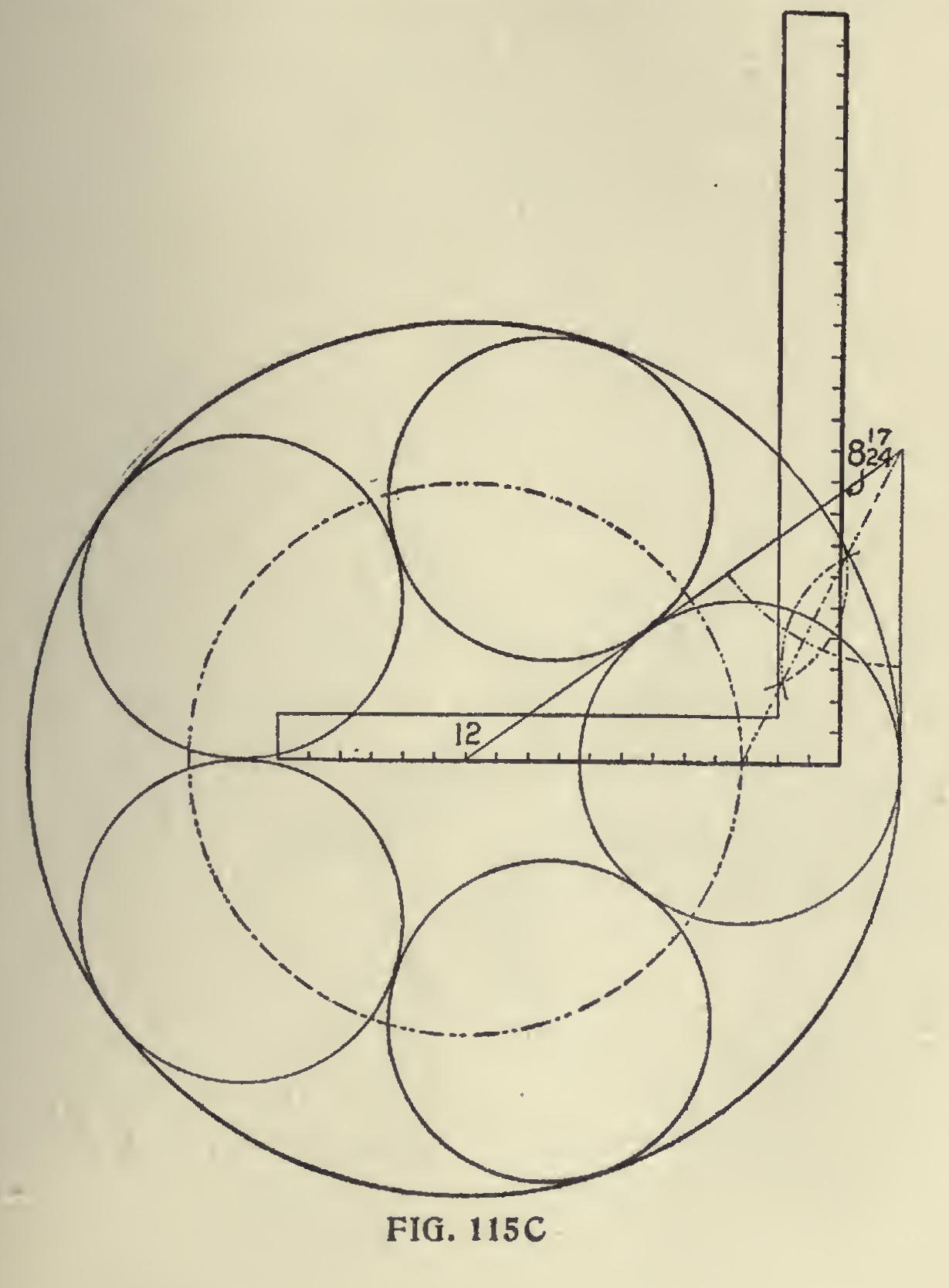
Polygons of any size may be drawn as shown in Fig. 115b. However, it is better to multiply the desired diameter by the decimal number given and reduce to feet and inches as follows : Suppose we wish to make a pentagon frame ten feet inscribed diameter, 10x8.72=87.20 inches, or 7 feet 3 and 5-24 inches will be the length of the sides. If we wish to put five circles inside of a large circle it may be done as shown in Fig. 115c. The given circle may be of any size and the figures used on the steel square are the same as those used in the preceding illustrations. From this it will be seen that it is the degree line that governs the layout of the diagram. If we wish to put four circles inside of a given circle then the degree line would rest at 45 degrees and intersect the blade at 12; or if we wish six circles, the degree line would rest at 30 degrees and the intersection on the blade would be at 6 and 11-12 inches.

If we wish to draw a five pointed star it may be done as shown in Fig. 116, and may be of any size desired by setting off the radius at a point directly above 12 on the tongue, and where the circum ference cuts the degree line as from 12 to A will be the proper spacing of the points of the star on the circumference.

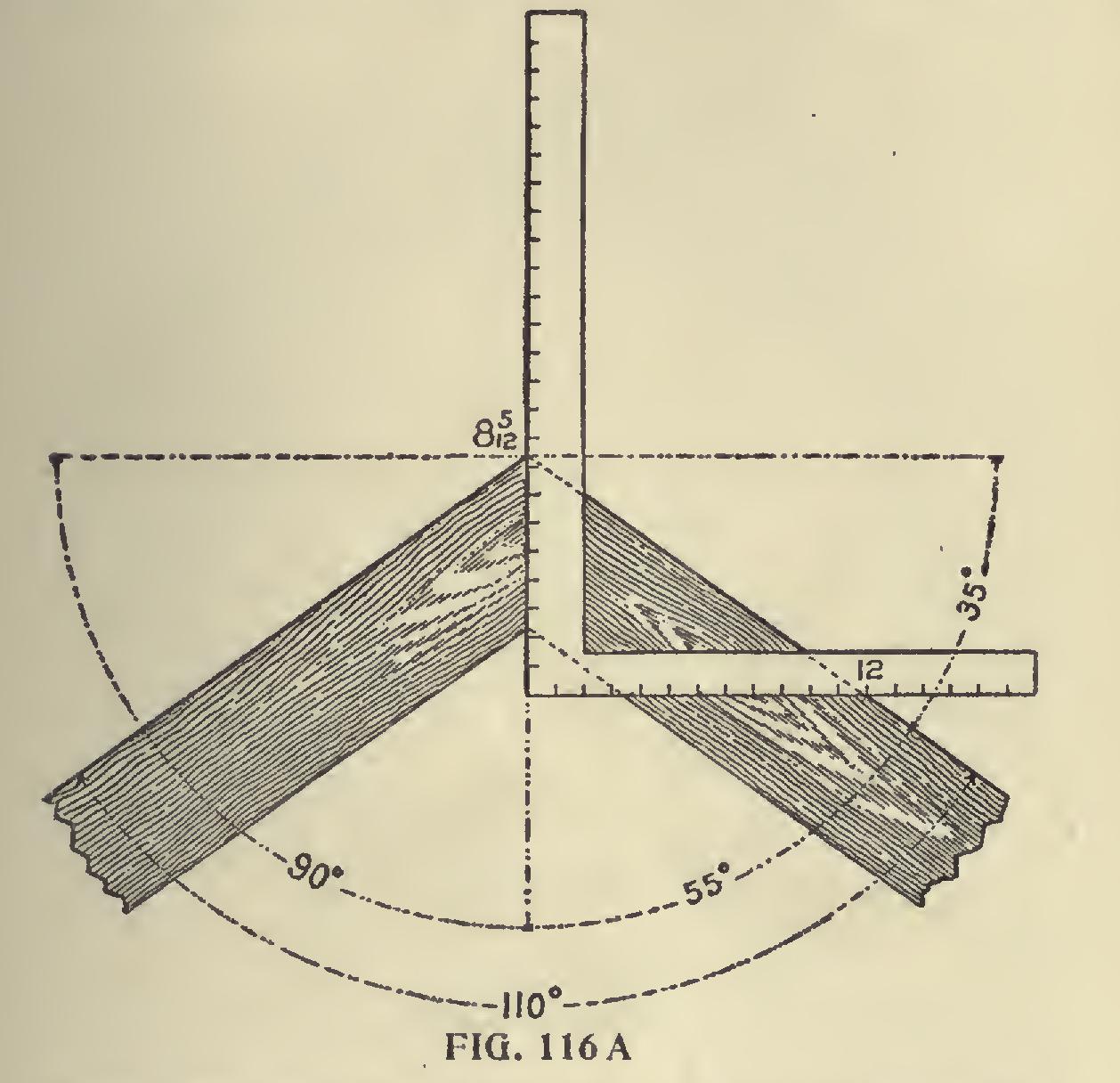
To Frame Timbers at Any Degree of Frame two pieces at an angle of 110 degrees. It is evident that the miter should stand at half way between the angle, or at 55 degrees and 55 degrees from 90 degrees leaves 35 degrees, and we find the tangent for 35 degrees is 8.4 (=8 and 5-12). Therefore, 12 on the tongue and 8 5-12 on the blade will give the miter, the blade giving the cut, as shown in Fig. 116a.

Though it may seem that some of these prob lems are of but little value on account of the small demand for their use, yet to know how to correctly handle the simpler forms is to know them all. It is true that the carpenter is not often called upon to frame polygonal roofs other than for the square or octagon shape, yet to be able to do so makes him a more finished and competent work man.

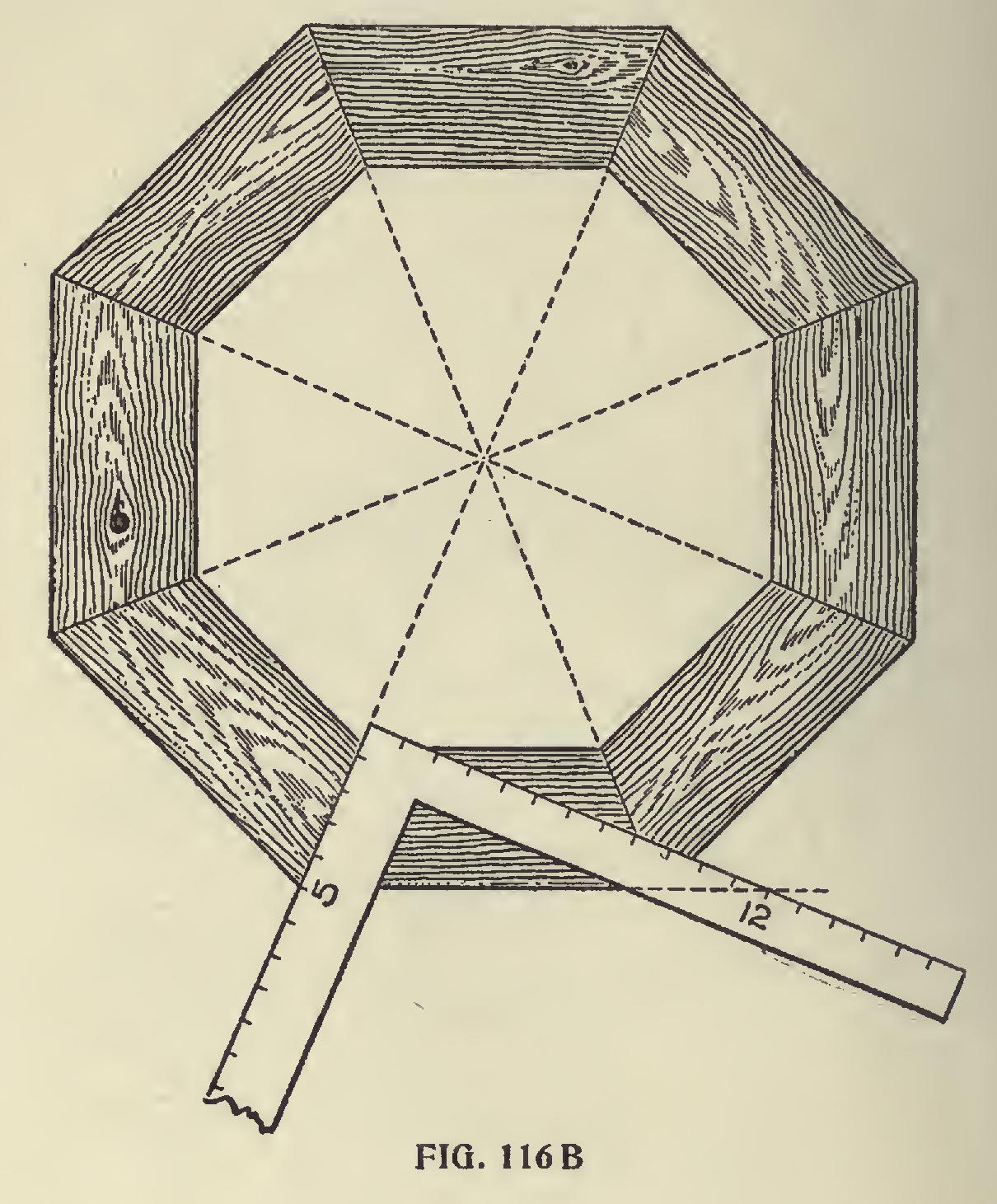
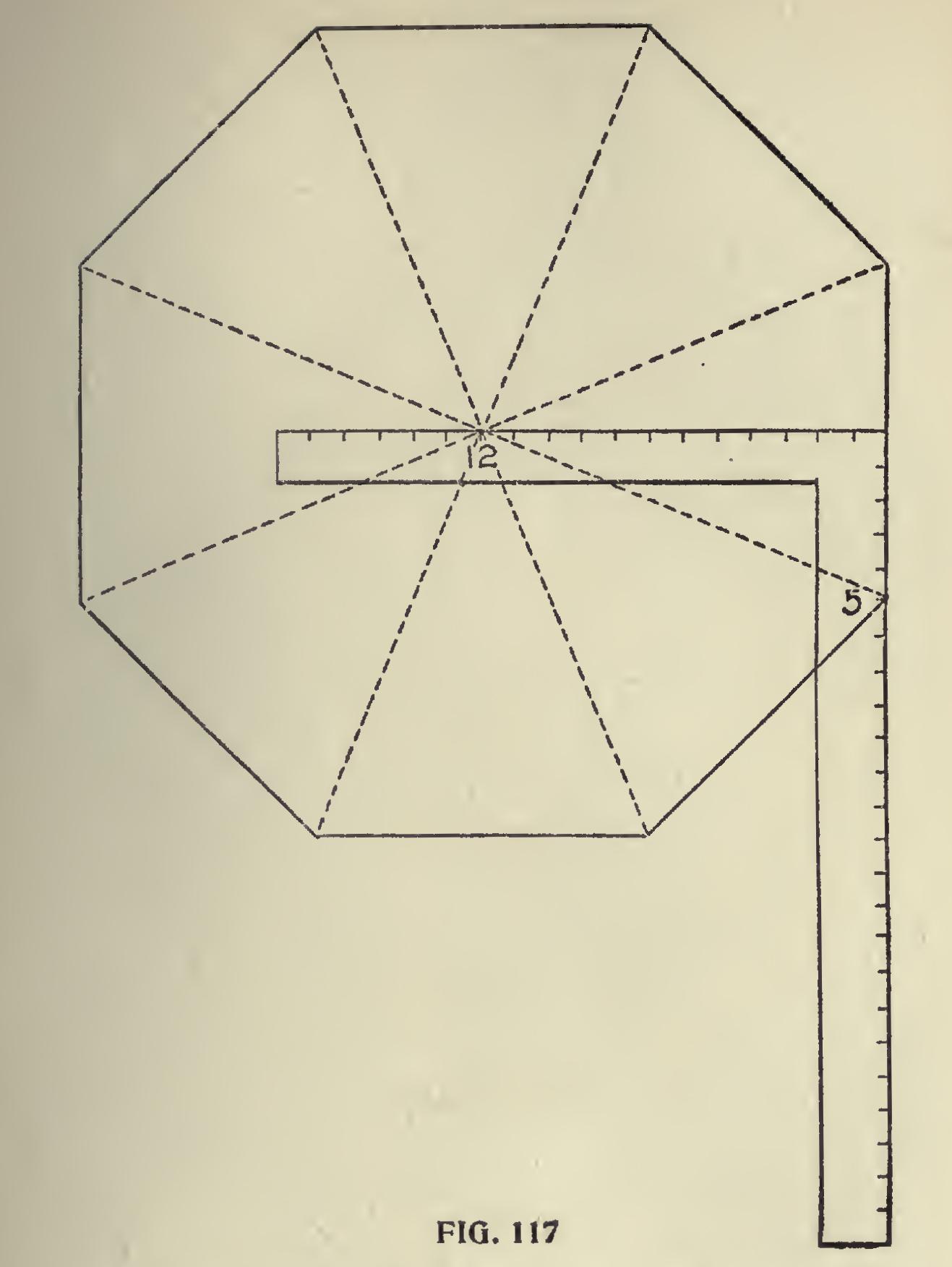
The Octagon for an Example.— With this in view we will take the octagon for an ex ample; we have found that 12 and 5 taken on the tongue and blade of the square give the miter as shown in Fig. 1168. These figures also form the angle that the hip rests with the common rafter as shown in Fig. 117. They also form the basis for all of the cuts. We also find for the true octagon the run of the hip diverges from the tongue 5 inches in a one foot run. Hence the side of an octagon one foot in diameter must be 5 inches at shown in Fig. 117A, or five-twelfths of its diameter.

This proportion always exists whether it be in ches, feet or yards. Thus the side of an octogan one inch in diameter would be five-twelfths of an inch. A 6-inch diameter would be 6x5-12= 30-12 or 21 inches, as shown in Fig. 117b.

Again from 12 to 5 measures 13 inches, a gain of one inch to one foot run of the common rafter, therefore the run of an octagon hip is one-twelfth longer than that of the common rafter.

The Curve for an Octagon Hip.—Now let us apply this proportion in developing the curve for an octagon hip.

In Fig. 117c draw BA. Place the square as shown, and draw line AC, and square down from B to C. AB is the run of the common rafter. A C is the run of the hip, and is one-twelfth longer than AB ; BC is equal to one-half the length of the plate, and is five-twelfths of the length AB. The whole figure bounded by A, B and C, is one-sixteenth of the plan, and is all that is necessary to draw.

Now, lay off the rise AD, and the desired curve for the common rafter, and draw any number of lines parallel with AB, from the rise to a few in ches beyond the curve of the common rafter. Now, measure these lines from rise to curve, and for each foot and fraction of a foot add to same line as many inches and twelfths of inches as there are feet and inches in length.

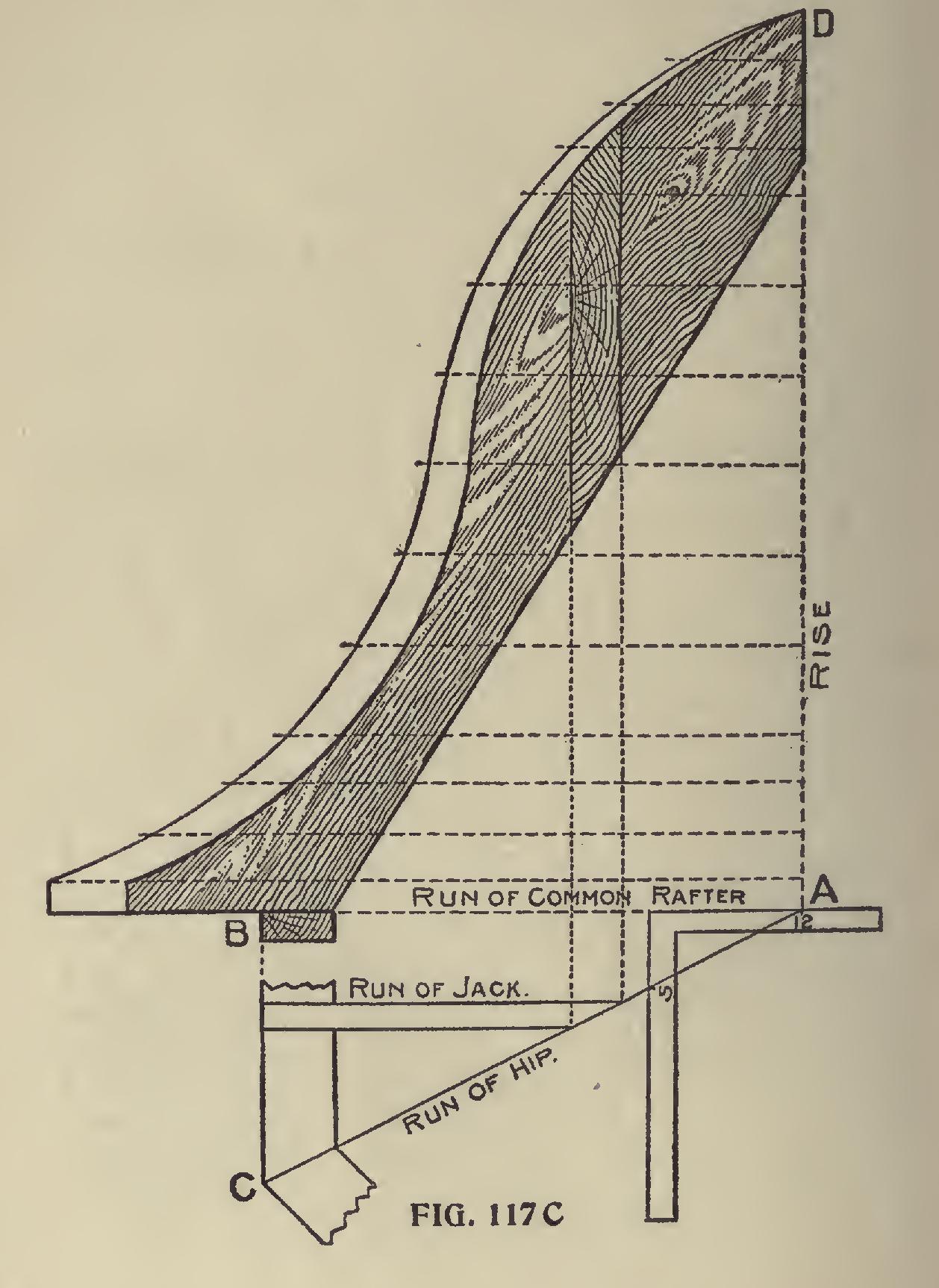
In other words, if a line 6 feet and 9 inches long, add to its length 6 and nine-twelfths inches and make a dot. After all lines have been thus measured, run an off hand curve through the dots, and the corresponding hip is determined.

To Find Shape of Jack.

The jack being a part of the common rafter, its shape is easily found by laying off the run and squaring up as shown.

It is thought better to run only the hips to center, and by using an octagon-shaped block or pole set with the sides, so that the hip will rest against it squarely, so as to get good nailing, as shown in Fig. 117d; besides letting the block extend above roof, furnishes an excellent stay for a finial.

To Find the Backing for a Curved Hip,

measure back from the face, on the horizontal lines, one-half the thickness of the hip and run an off hand curve, as previously done for the face line, and this will be the proper gauge line along the side of the hip. It is very important that the hips should be backed in roofs of this kind, because the shape is ever changing and the backing should corre spond.

Steel Square