Polygons and Miters

POLYGONS AND MITERS In the following paragraphs we present still further examples of the application of the steel square to the solution of problems that are to a greater or less extent of a mathematical nature, some of which are ordinarily solved only by the methods of geometry or trigonometry.

Polygons Inscribed in Circles.

In the follow ing table, set the bevel to the pair of numbers under the polygon to be inscribed.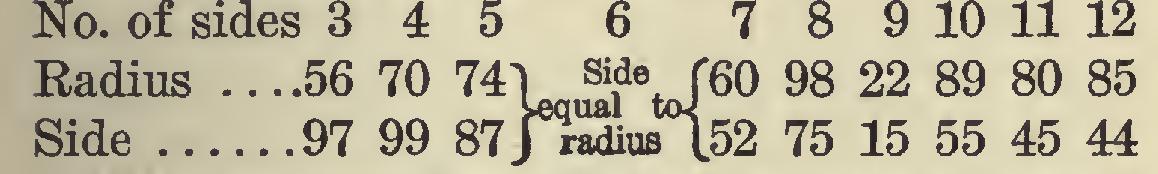

If we require the radius of a circle which will circumscribe an octagon 8 inches on a side, we refer to column 8, take 98 parts on the blade and 75 on tongue, and tighten the bevel. As the side of a hexagon equals the radius of its circle, the side of an octagon must be less than the radius; hence we shift to 8 inches, that end of the bevel blade which gives the lesser number, in this case, on the tongue of the square, as the 75 parts to which the bevel was set are less than the 98. The required radius is then indicated on the blade.

We will now explain the figures used in step ping round a circle forming inscribed polygons from three to twelve sides: Set bevel or fence to 12 on blade, and the number opposite each poly gon on tongue; move to diameter of circle; answer of the side of polygon on tongue.

Triangle 3 10.40 Square 4 8.49 Pentagon 5 7.05 Hexagon 6 6.00 Heptagon ... .... 7 5.21 Octagon 8 4.60 Nonagon 9 4.11 Decagon. 10 3.71 Undecagon 11 3.39 Dodecagon . . . 12 3.11 To Divide a Circle into a Given Number of Parts, multiply the corresponding number in column one and the product is the chord to lay off on the circumference. The side of the polygon being known, to find the radius of a circle that will circumscribe: Multiply the given side by the cor responding number opposite of polygon in column two.

No. of Names of Angle of Sides Polygons Angle Polygon Column 1 Column 2 3 Triangle 120 60 1.732 .5773 4 Square. 90 90 1.414 .7071 5 Pentagon 72 108 1.175 .8510 6 Hexagon , 60 120 Radius Side 7 Heptagon . 514- 1284 .8677 1.1520 8 Octagon . 45 135 .7653 1.3071 9 Nonagon , . 40 140 .6840 1.4863 10 Decagon, 36 144 .6180 1.6181 11 Undecagon 32-N .5634 1.7754 12 Dodecagon 30 150 .5176 1.9323

The Side of a Polygon Being Known, to Find the Length of Perpendicular.—Set bevel or fence to the tabulated numbers below. Example: The side of an octagon is 12, set bevel to 23 on tongue, on blade. Blade gives the answer.

No. of Sides.. .3 4 5 6 7 8 9 10 11 12 Perpendi cular . .9 1 30 13 27i 50i 281 51-1 26 Side of .

Polygon .314 2 351 15 26 23 37 18i 30i 14 Foundation of Miters.—We said that it was in the division of the circle that the whole subject of miters is founded, whether regular or irregular, and we believe there is no better way of illustrating this point than as shown in Fig. 181. If there is any one of the illustrations that we feel a little bit prouder of than the others, it would fall to this one.

In this figure are shown a number of the regular polygons. Here they are beginning with the triangle in their order up to twelve, then they skip to fifteen and they could keep on growing in number of sides until their lengths would repre sent only a very small fractional part of an inch. There is a whole lot of practical information that may be gathered from this illustration.

By dividing 360 (the number of degrees in a circle), by the number of sides in the desired polygon will give the angle that the miters stand with each other, but in order to obtain the angle on the steel square, it is only necessary to divide 180 by the number of the sides in the polygon and the quotient will represent the angle in degrees to use on the steel square to obtain the miter. The blade giving the cut. The figures used on the blade also give the length of the sides of the polygon when the inscribed diameter is one foot. These figures are also used for cuts in roof work.

Fractional Value of Decimals.—The following fractional numbers represent the value of the deci mal numbers shown on the degree lines and are the figures to use on the blade as follows: triangle, 20 19-24; square, 12; pentagon, 8 17-24; hexagon, 6 11-12; heptagon, 5 19-24; octagon, 4 23-24; nonagon, 4$; decagon, 3 11-12; undecagon, 31; dudecagon, 3 5-24; quindecagon, 2 13-24.