Oogenesis and Spermatogenesis Reduction of the Chromosomes

Balfour probably stated the exact truth when he said, " In the formation of the polar cells part of the constituents of the germinal vesicle, which are requisite for its functions as a complete and independent nucleus, is removed to make room for the supply of the necessary parts to it again by the spermatic nucleus " ('8o, p. 62). He fell, however, into the same error as Minot and Van Beneden in characterizing the germ-nuclei as " male " and " female." 2 Cher die Bedeutung der Kerntheilungsfiguren.

"ids," the latter being identified with the visible chromomeres or chromatin-granules. The ids finally are associated in linear groups to form the " idants " or chromosomes. Since the biophores differ qualitatively, it follows that the same must be true of the higher units formed by their aggregation. Hence each chromosome has a distinct and definite character of its own, representing a particular group of hereditary qualities. From this it follows that the number of 1 For division of the spermatogonia see Fig. 39 ; for the corresponding phenomena in var. univalens see Fig. 107.

specifically distinct chromosomes is doubled by the union of two germ-cells, a process which if unchecked would quickly lead to an infinite complexity of the chromatin or germ-plasm. The end of maturation, or reduction, is therefore to prevent " the excessive accumulation of different kinds of hereditary tendencies or germplasms " I through the progressive summation of ancestral chromatins.

We now come to the vital point of Weismann's hypothesis of reduction, about which all later researches have revolved. Assuming with Roux that the different qualities or " ancestral germ-plasms " are arranged in a linear manner in the spireme-thread and in the chromosomes derived from it, he ventured the prediction ('87) that two kinds of mitosis would be found to occur. The first of these is characterized by a longitudinal splitting of the thread, as in ordinary cell-division, " by means of which all the ancestral germ-plasms are equally distributed in each of the daughter-nuclei after having been divided into halves." This form of division, which he called " equal division " (Aequationstheilung), was then a known fact. The second form, at that time a purely theoretical postulate, he assumed to be of such a character that each daughter-nucleus should receive only half the number of ancestral germ-plasms possessed by the mother-nucleus. This he termed a "reducing division" (Reduktionstheilung), and suggested 2 that this might be effected either by a transverse division of the chromosomes, or by the divergence and separation of entire chromosomes without division. By either method the number of " ids " would be reduced ; and Weismann argued that such reducing divisions must be involved in the formation of the polar bodies, and in the parallel phenomena of spermatogenesis.

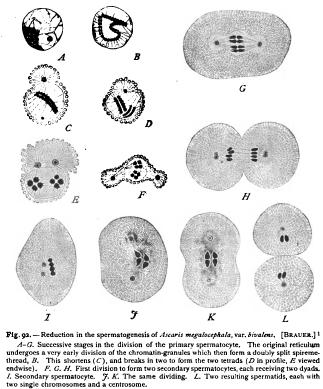
The fulfilment of Weismann's prediction is one of the most interesting results of recent cytological research. It has been demonstrated, in a manner which I believe is incontrovertible, that the reducing divisions postulated by Weismann actually occur, though not precisely in the manner conceived by him. Unfortunately, however, this demonstration has been made in only a few specific cases, — the complete demonstration, indeed, in but a single group, namely, the copepod crustacea, — while careful studies by the most accomplished observers have led to an entirely different result in other cases; namely, in Ascaris and the flowering plants. We are in fact confronted by an apparent contradiction of so absolute a character that no middle ground between the conflicting results can at present be discovered. We may best appreciate the nature of this contradiction by a preliminary consideration of the tetrad groups ; for it is plain that the nature of the maturation-divisions can only be approached through a study of the origin of the tetrads.