Roofs and Roof Construction

To find the dimensions of struts: Rule.—Multiply the square root of the length supported, in feet, by the length of the strut in feet, and the square root of the product multi plied by .8 will give the depth; which multiplied by .6 will give the thickness.

In a Queen=Post Roof.

To find the dimensions of the principal rafters: Rule.—Multiply the square of the length in feet by the span in feet, and divide the product by the cube of the thickness in inches; the quo tient multiplied by .155 will give the depth.

To find the dimensions of the tie=beam: Rule.—Divide the length of the longest un supported part by the cube root of the breadth, and the quotient multiplied by 1.47 will give the depth.

To find the dimensions of the queen=posts: Rule.—Multiply the length in feet of the post by the length in feet of that part of the tie-beam it supports: the product multiplied by .27 will give the area of the post in inches; and the breadth and thickness can be found as in the king-post. The dimensions of the struts are found as before.

To find the dimensions of a straining beam: Rule.—Multiply the square root of the span in feet by the length of the straining beam in feet, and extract the square root of the product; mul tiply the result by .9, which will give the depth in inches. The beam, to have the greatest strength, should have its depth to its breadth in the ratio of 10 to 7 ; therefore, to find the breadth, multiply the depth by .7.

To find the dimensions of purlins: Rule.—Multiply the cube of the length of the purlin in feet by the distance the purlins are apart in feet, and the fourth root of the product will be the depth in inches, and the depth multiplied by .6 will give the thickness.

To. find the dimensions of the common rafters when they are placed 12 inches apart : Rule.—Divide the length of bearing in feet by the cube root of the breadth in inches, and the quotient multiplied by .72 will give the depth in inches.

Beams acting as struts should not be cut into or mortised on one side, so as to cause lateral yielding.

Purlins should never be framed into the princi pal rafters, but should be notched. When notched they will carry nearly twice as much as when they are framed.

Purlins should be in as long pieces as possible. Rafters laid horizontally are very good in con struction and cost less than purlins and common rafters.

The ends of tie-beams should be kept with a free space around them to prevent decay.

It is an injudicious practice to give an excess ive camber to the tie-beam; it should only be drawn up when deflected, as the parts come to their bearings.

The struts should always be immediately un derneath that part of the rafter wheron the purlin lies.

The diagonal joints of struts should be left a little open at the inner part, to allow for the shrinkage of the heads and feet of the king and queen posts.

It should be specially observed that all cranks or bends in iron ties are avoided.

And, as an important final maxim, every con struction should be a little stronger than strong enough.

Flip=roofs.

The principles to be determined in a hip roof are eight, namely : 1st. Span or width of building to be roofed.

2d. Run of the building, which is one-half the span.

3d. The rise given the common rafter.

4th. The angle that the common rafter makes with the level of the plate; that is, the pitch of the roof.

5th. The length of the common rafter.

6th. The angle that the hip-rafter makes with the adjoining sides of the roof.

7th. The length of the hip-rafters.

8th. The distance from the corner of the build ing to the center line of the first jack ; that is, the common difference.

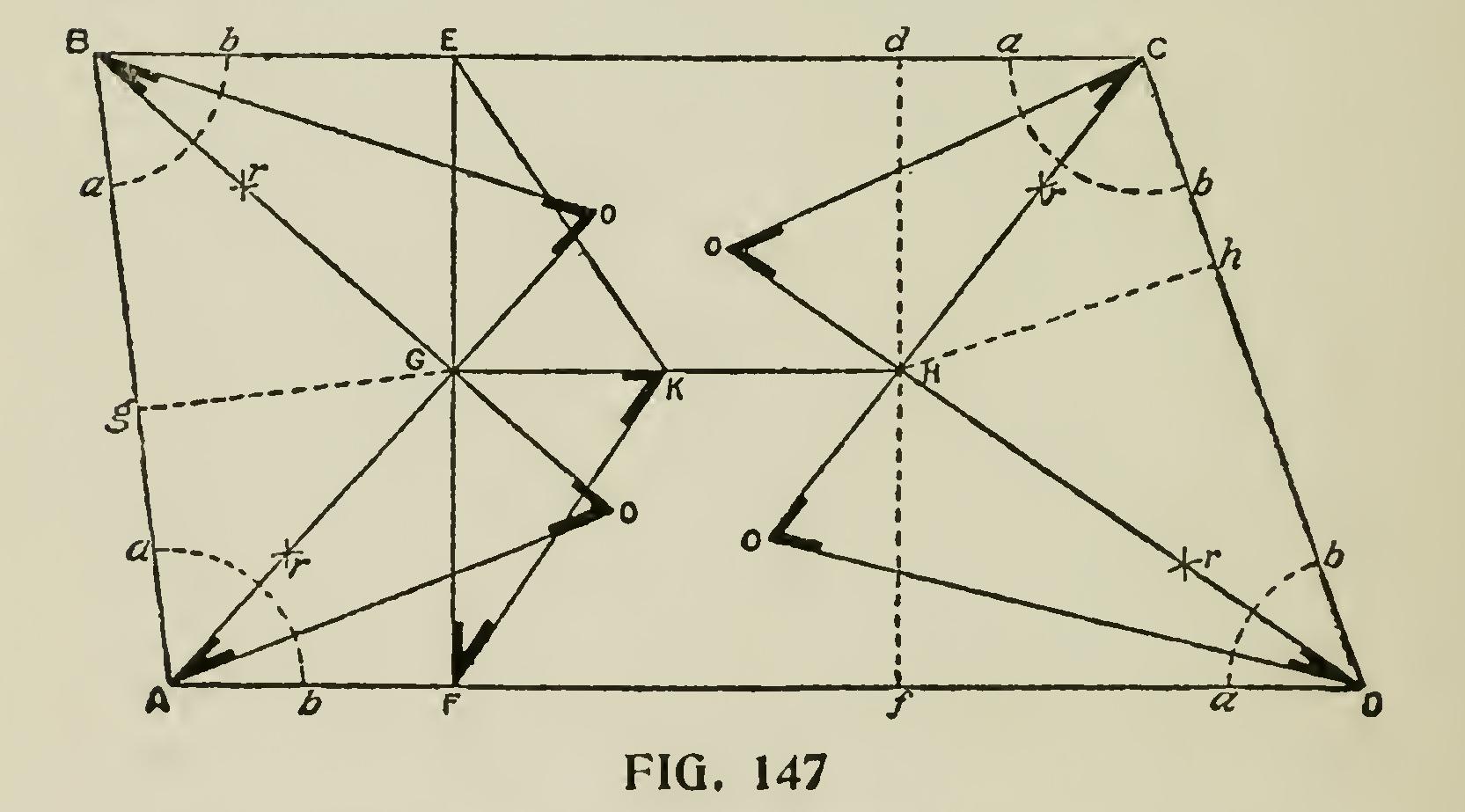
The 1st, 2d and 3d being given the others may be found, as will be shown in the following illus trations : Let ABCD, Fig. 147, be the plan of the roof. Draw GH parallel to the sides, AD, BC, and in the middle of the distance between them. From the points A, B, C, D, with any radius, describe the curves ab, ab, cutting the sides of the plane at a, b. From these points, with any radius, bisect the four angles of the plan at r, r, r, r, and from A, B, C, D, through the points, r, r, r, r, draw the lines of the hip rafters, AG, BG, CH, DH, cutting the ridge line, GH, in G and H, and pro duce them indefinitely. The cross lines, EF, df, are the seats of the last entire common rafters. Through point in the ridge-line, make GK equal to the height or rise of roof, and join EK, FK; then EK is the length of the common rafter. Make Go, Ho, equal to GK, the rise of the roof, and join Ao, Bo, Co, Do, for the length of the hip rafters. If the triangles, AoG, Bog, be turned round their seats, AG, BG, until their perpendicu lars are perpendicular to the plane of the plan, the points, 00, and the lines Go, Go, will coincide, and the rafters, Ao, Bo, be in their true positions.

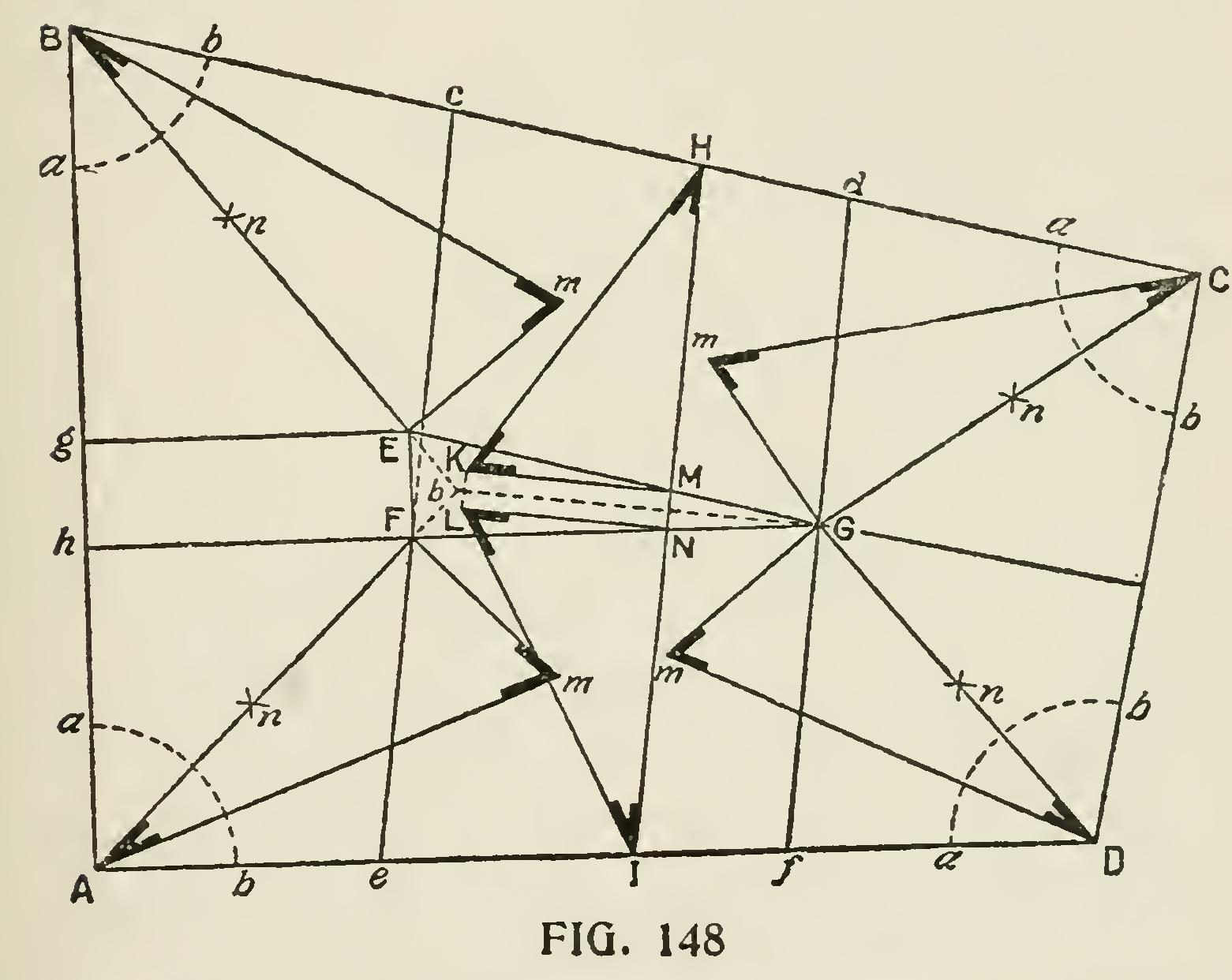
If the roof is irregular, and it is required to keep the ridge level, we proceed as shown in Fig. 148.

Bisect the angles of the two ends by the lines Ab, Bb, CG, DG, in the same manner as in Fig. 147; and through G draw the lines GE, GF, parallel to the sides, CB, DA, respectively, cutting Ab, Bb, in E and F; join EF; then the triangle EGF, is a flat, and the remaining triangle and trapeziums are the inclined sides. Join Gb, and draw HI perpendicular to it; at the points M and N, where HI cuts the lines GE, GF, draw MK, NL perpendicular to HI, and make them equal to the rise; then draw HK, IL for the lengths of the common rafters. At E, set up Em perpendicular to BE; make it equal to ME or NL, and join Bm, for the length of the hip rafter, and proceed in the same manner to obtain Am, Cm, Dm.

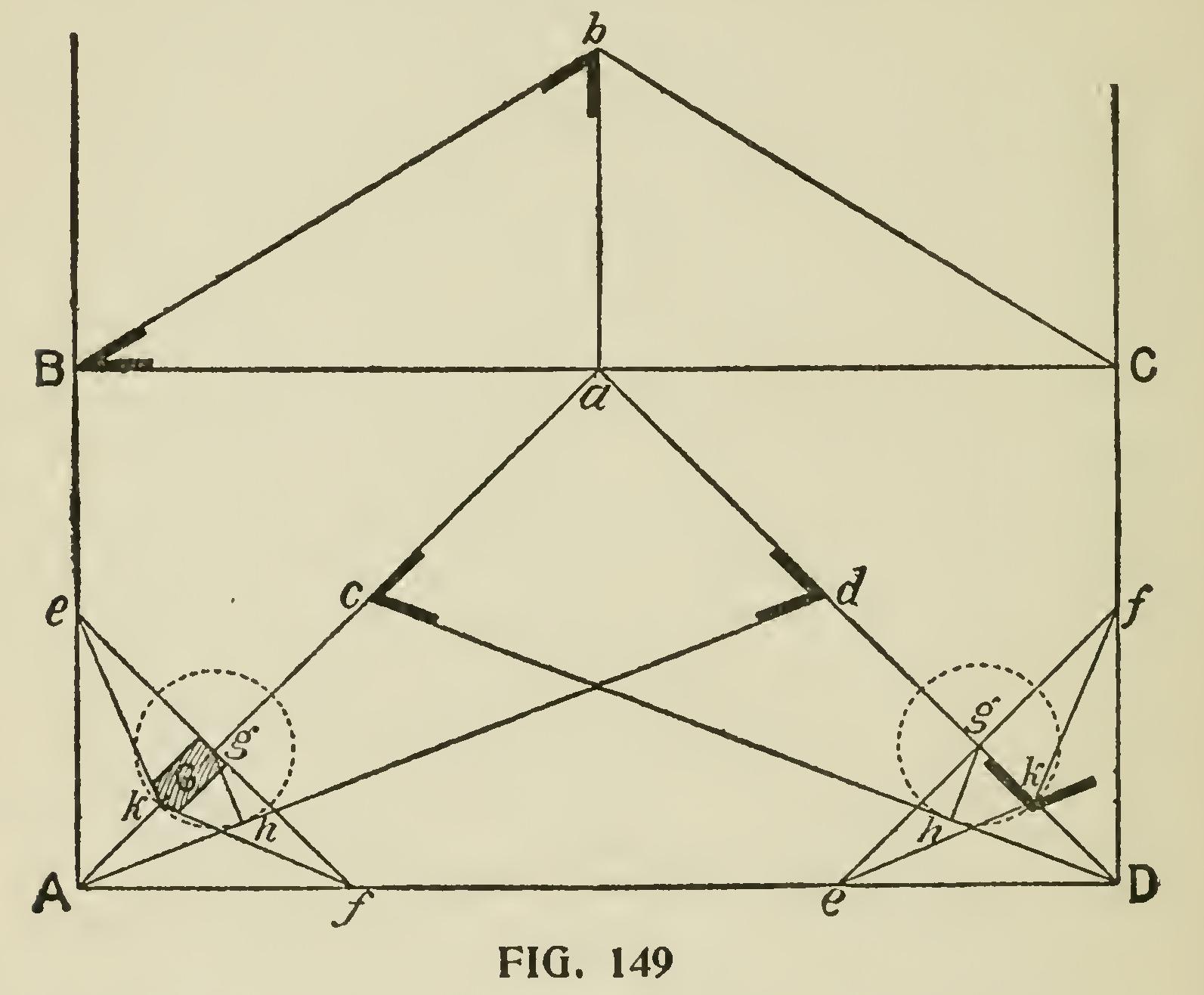
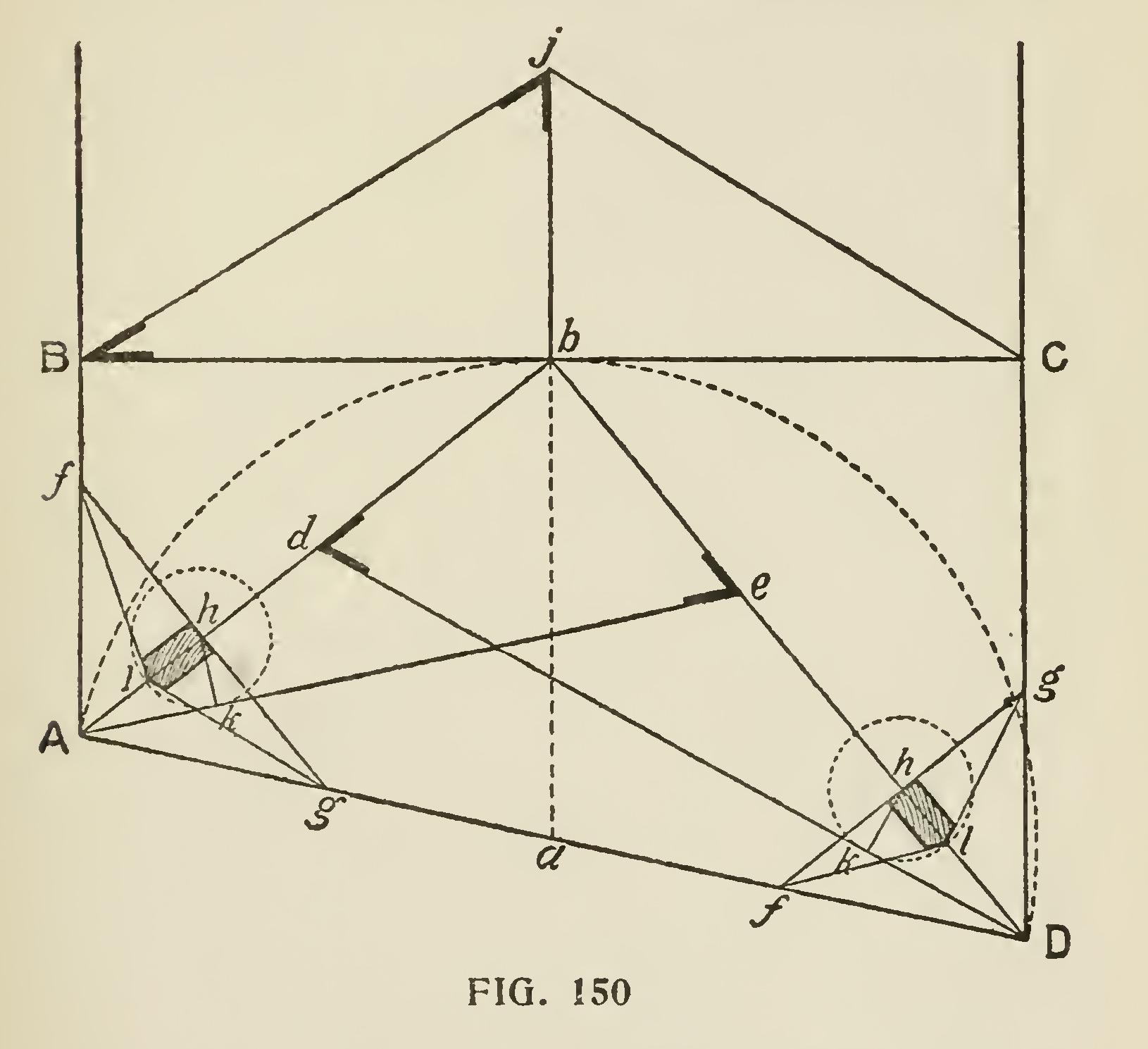
To find the backing of a hip rafter, when the plan is right-angled, we proceed as shown in Fig. 149. Let Bb, bC be the common rafters, AD the width of the roof, and AB equal to one-half the width. Bisect BC in a, and join Aa, Da. From a set off ac, ad equal to the height of the roof ab, and join Ad, Dc; then Ad, Dc are the hip rafters. To find the backing from any point h in Ad, draw the perpendicular hg, cutting Aa in g ; and through g draw perpendicular to Aa the line ef, cutting