Right Jack Fig21

RIGHT JACK FIG.21 run of the right common rafter on the tongue. Blade gives the cut of the left jack. Vice versa for the right jack. Figs. 20 and 21 illustrate these cuts.

Projecting Cornice.—Here is another problem that comes in connection with the uneven pitched roof. Where a projecting cornice is desired, with planceer, the valley will not rest on the angle of the plate, but at a point in line with the inter section of the cornice.

This necessitates the plate on the steeper pitch being raised as much as the difference in the rise of the pitches; in the width of the cornice.

Thus, if the cornice be 18 inches wide, the rise of the half pitch is 18 inches, and that of the one third pitch is 12 inches, a difference of six inches. Therefore the proper height of the plate above that of the lower pitch is six inches.

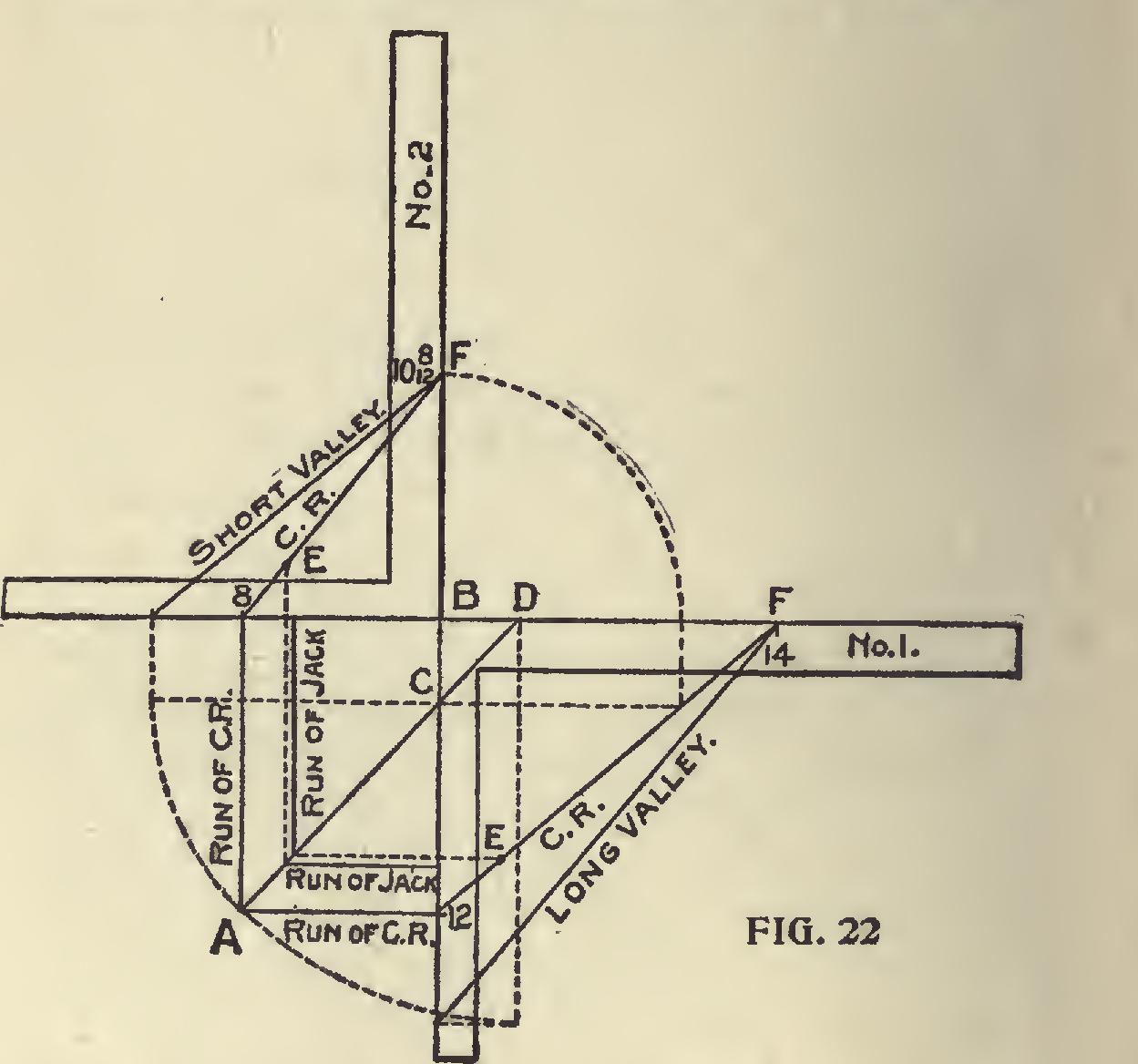
To Find the Length of Rafters Where the Rises in the Roof are of Different Height; for example, we will suppose the main gable, Fig. 22, to be 24 feet wide with a 14-foot rise, and the side gable to be 16 feet wide with a 10-foot 8-inch rise. In a case of this kind it is better to let one of the valleys extend on up to the ridge board of the main gable and let the other valley rest against it (the long valley). But how to locate them on the square is the main question. 1st. Place the squares as shown. On square No. 1 lay off the run and rise of the wide gables, and the same for the narrow gable on square No. 2.

2d. By connecting the run and the rise, as shown by the diagonal line on each of the squares will be the length of the common rafter.

3d. Square out from the tongue as shown, till they intersect at A, which will be the runs of the gables or of the common rafters.

4th. Set compasses at B, and open to equal the rise of the narrow gable and swing to the blade of No. 1, and square in to the common rafter, thence run an imaginary line parallel to the blade, and where it intersects the tongue establishes the point where the ridge of the narrow gable or dies intersects on main roof and which point we will call C.

5th. A line drawn from A to C represents the run of the short valley and by ex tending the line on to the blade of No. 1 establishes point D, from which to B, represents the run of the long valley, and these lengths taken on the tongues as shown, and connected with their respective rises, will be lengths.

6th. The lengths of the jacks are found as shown from E to F, which we trust is clear enough without fur ther explanation.

The cuts and bevels are all contained in this dia gram.

The Pitch of the Tower Roof may be obtained along with all the bevel lines by the proper use of the steel square, as shown in Fig. 23, which illustrates some unus ual pitches. It is evident that if the run of 1 foot is 12 inches, the span must be double that or 24 inches; therefore the rise must be that proportion of the span. Then the first inch in rise is one-twenty fourth, the second one-twelfth, the third one eighth, etc. The twenty-fourth inch rise being equal the span, it is therefore one pitch. As the rise continues above this point, it is simply a rep etition of the above with a 1 prefixed, thus : The twenty-fifth inch rise being one and one-twenty fourth pitch, etc. ; but we are now beyond the limits of the full scale as applied to the square, so we must reduce the scale. By letting the vertical line B represent the blade we will have reduced the scale one-half. The pitches would center at 6 on the tongue instead of 12, as in the full scale. We must now use the half inches above 12 on the blade for each rise of one inch till we reach the twenty-fourth inch, which will be equal to two pitches or 48-inch rise to the foot. For steeper pitches it is necessary to again change the scale. If we let the blade rest at A the pitches will center at 3 on the tongue (making the scale size), and by letting the inches above 12 on the blade represent the full inches in rise will give the cuts, etc., from the forty-eighth inch rise to the ninety-sixth inch rise to the foot, or 4 pitches.