Practical Carpentry

Problem 12.—To describe a square equal to any number of given squares: Let it be required to construct a square equal to three given squares A, B and C (Fig. 35). Take the line DE, equal to the side of the square C. From the extremity D erect DF perpendicular to DE, and equal to the side of the square B: join EF; then a square described upon this line will be equal to the sum of the two given squares C and B. Again, upon the straight line EF erect the perpendicular FG, equal to the side of the third square A; and join GE, which will be the side of the square GEHK, equal in area to A, B and C. Proceed in the same manner for any given number of squares.

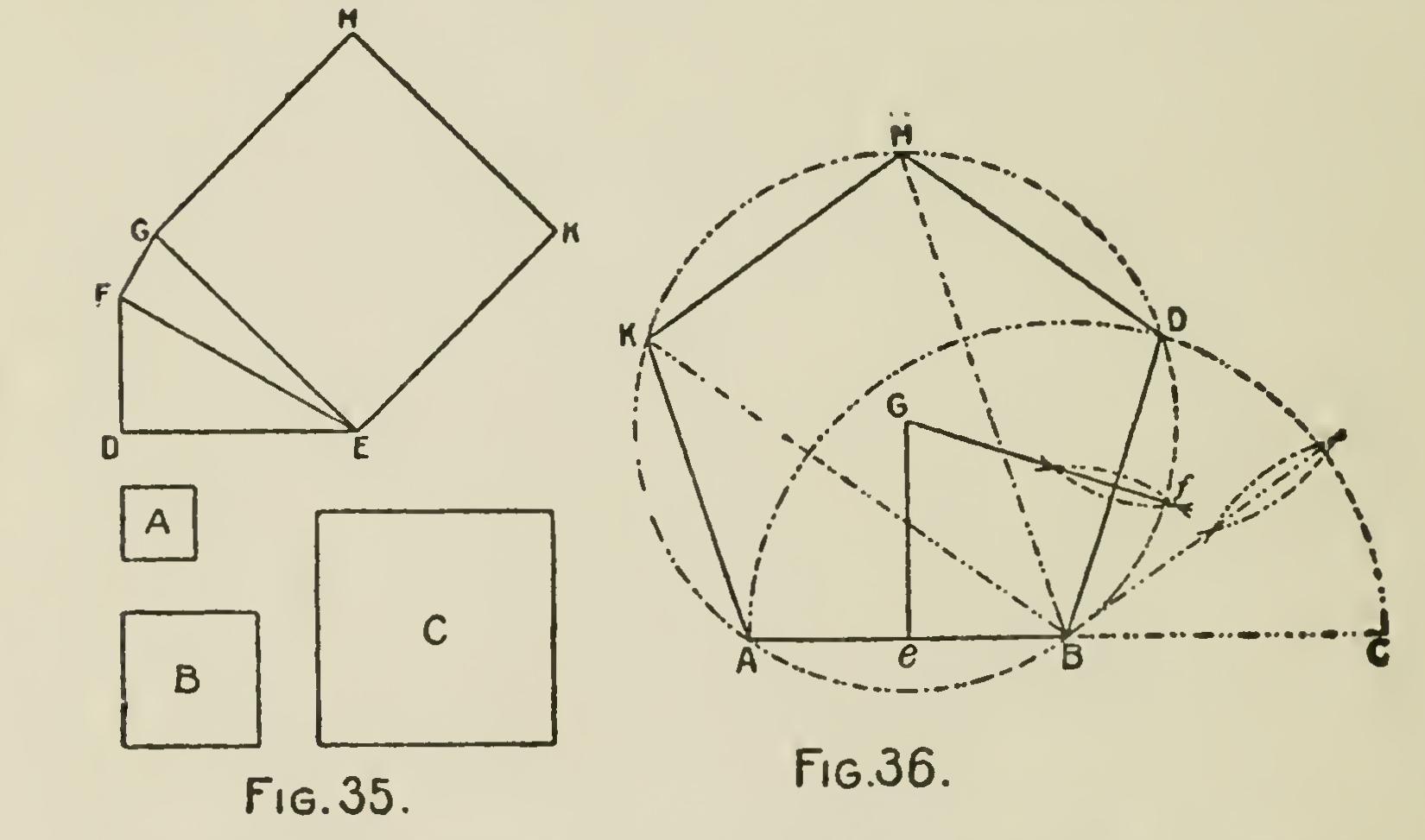
Problem 13.—Upon a given straight line to describe a regular polygon: To produce a regular pentagon draw AB to C (Fig. 36), so that BC may be equal to AB ; from B as a center, with the radius BA or BC describe the semicircle ADC; divide the semi-circumference ADC into as many equal parts as there are parts in the required poly gon, which, in the present case, will be five; through the second division from C draw the straight line ED, which will form another side of the figure. Bisect AB at e, and BD at f, and draw eG and fG perpendicular to AB and BD ; then G, the point of intersection, is the center of a circle, of which AB and D are points in the cir cumference. From G, with a radius equal to its distance from any of these points, describe the circumference ABDHK; then producing the dot ted lines from the center B, through the remain ing divisions of the semicircle ADC, so as to meet the circumference of which G is the center, in H and K, these points will divide the circle ABDHK into the number of parts required, each part being equal to the given side of the penta gon.

From the preceding example it is evident that polygons of any number of sides may be constructed upon the same principles, because the circumference of all circles, when divided into the same number of parts, produce equal angles; and, consequently, by dividing the semi-circum ference of any circle into the number of parts required, two of these parts will form an angle which will be subtended by its corresponding parts of the whole circumference. And as all regular polygons can be inscribed in a circle, it must necessarily follow, that if a circle be de scribed through three given angles of the poly gon, it will contain the number of sides or angles required.

The above is a general rule by which all regular polygons may be described upon a given straight line; but there other methods by which many of them may be more expeditiously con structed, as shown in the following examples : Problem 14.—Upon a given straight line to

describe a regular pentagon: Let AB (Fig. 37) be the given straight line; from its extremity B erect Bc perpendicular to AB, and equal to its half. Join Ac, and produce it till cd be equal to Bc, or half of the given line AB. From A and B as centers, with a radius equal to Bd, describe arcs intersecting each other in e, which will be the center of the circumscribing circle ABFGH. The side AB, applied successively to this circum ference, will give the angular points of the penta gon; and these being connected by straight lines will complete the figure.

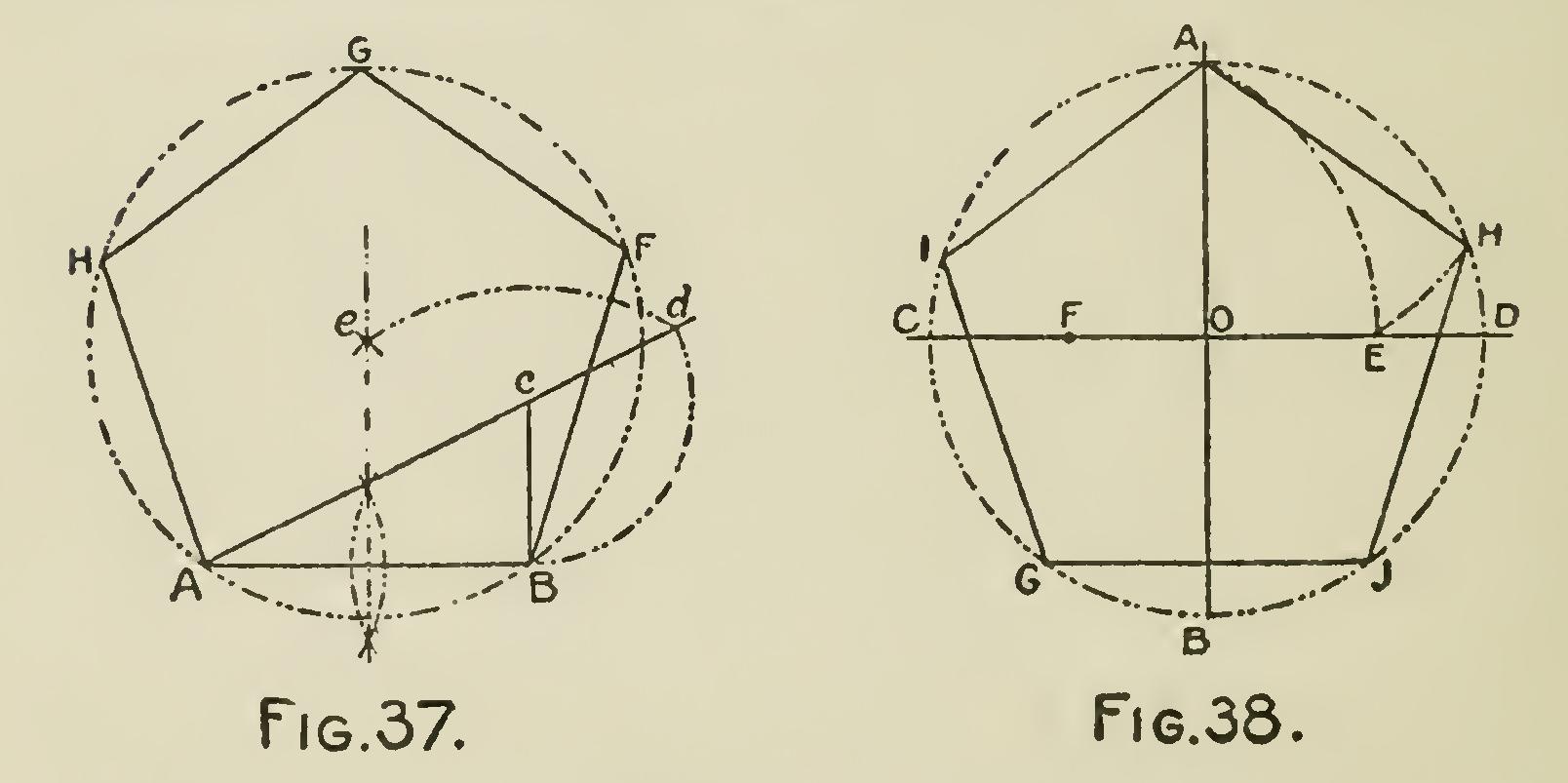
Problem 15.—Another method of inscribing a pentagon in a circle: In Fig. 38, draw two dia meters AB and CD, at right angles to each other, as at 0. From 0 as center describe the desired circumference. Bisect the radius C 0 at F ; with F as a center and FA as a radius, describe the arc cutting 0 D at E. With A as a center and AE as a radius, describe the arc HE cutting the cir cumference of the circle at H, with the same radius describe an arc cutting the circumference of the circle at I. With these points as centers and using the same radius AE describe arcs cut ting the circumference of the circle at J and G. Join HAIG and J and we have the inscribed regular pentagon.

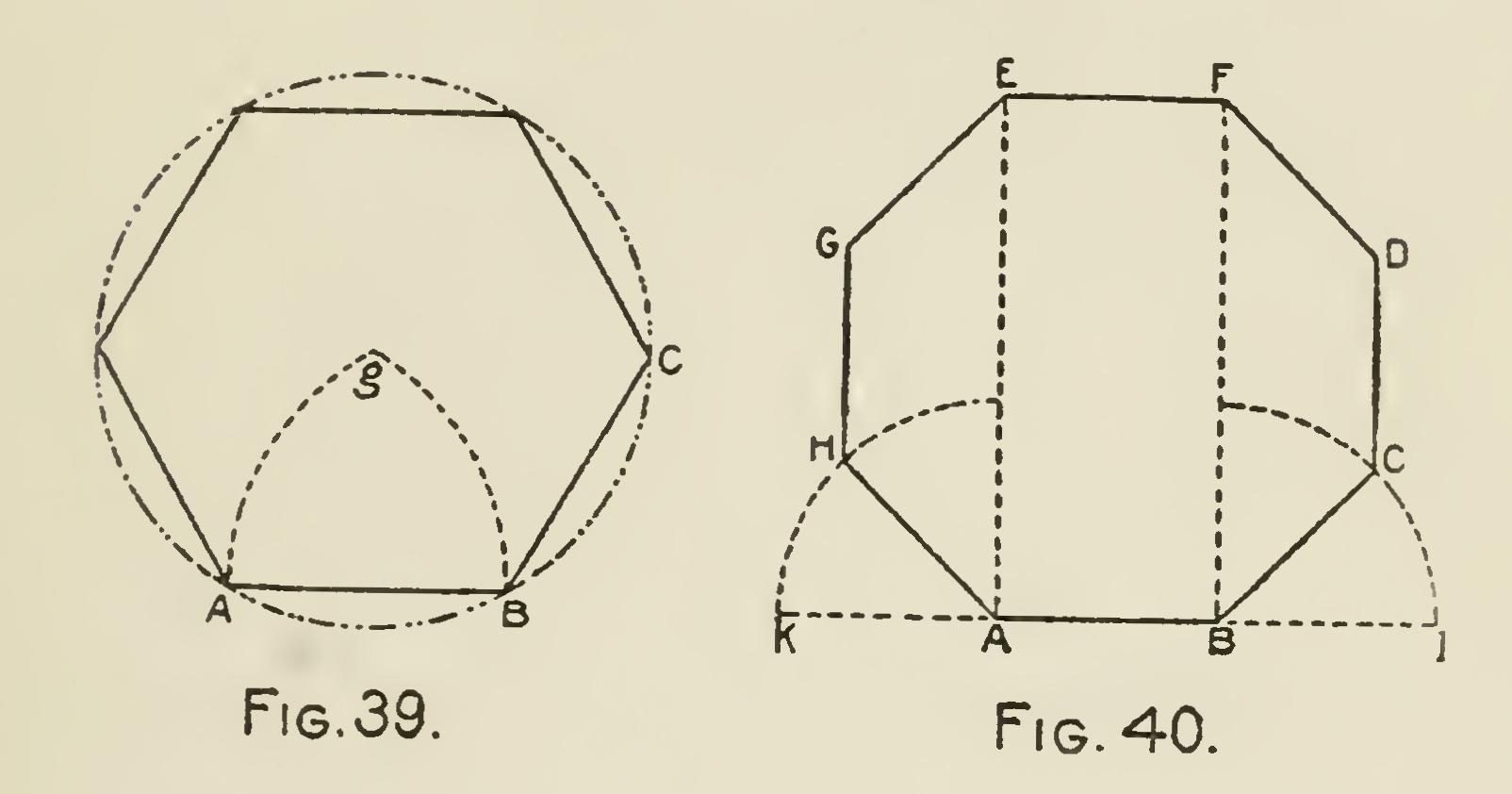
Problem 16.—Upon a given straight line describe a regular hexagon: Let AB (Fig. 39) be the given straight line. From the extremities A and B as centers, with the radius AB, describe arcs cutting each other in g. Again, from g, the point of intersection, with the same radius, describe the circle ABC, which will contain the given side AB six times when applied to its cir cumference, and will be the hexagon required.

Problem 17.—To describe a regular octagon upon a given straight line: Let AB (Fig. 40) be the given line. From the extremities A and B erect the perpendiculars AE and BF; extend the given line both ways to k and 1, forming external right angles with the lines AE and BF. Bisect these external right angles, making each of the bisecting lines All and BC equal to the given line AB. Draw JIG and CD parallel to AE or BF, and each equal in length to AB. Draw from G, GE parallel to BC, and intersecting AE in E, and from D draw DF parallel to All, intersecting BF in F. Join EF, and ABCDFEGH is the octagon required. Or from D and G as centers, with the given line AB as radius, describe arcs cutting the perpendiculars AE and BF in E and F, and join GE, EF, FD, to complete the octagon.