Hoppers and Hopper Bevels

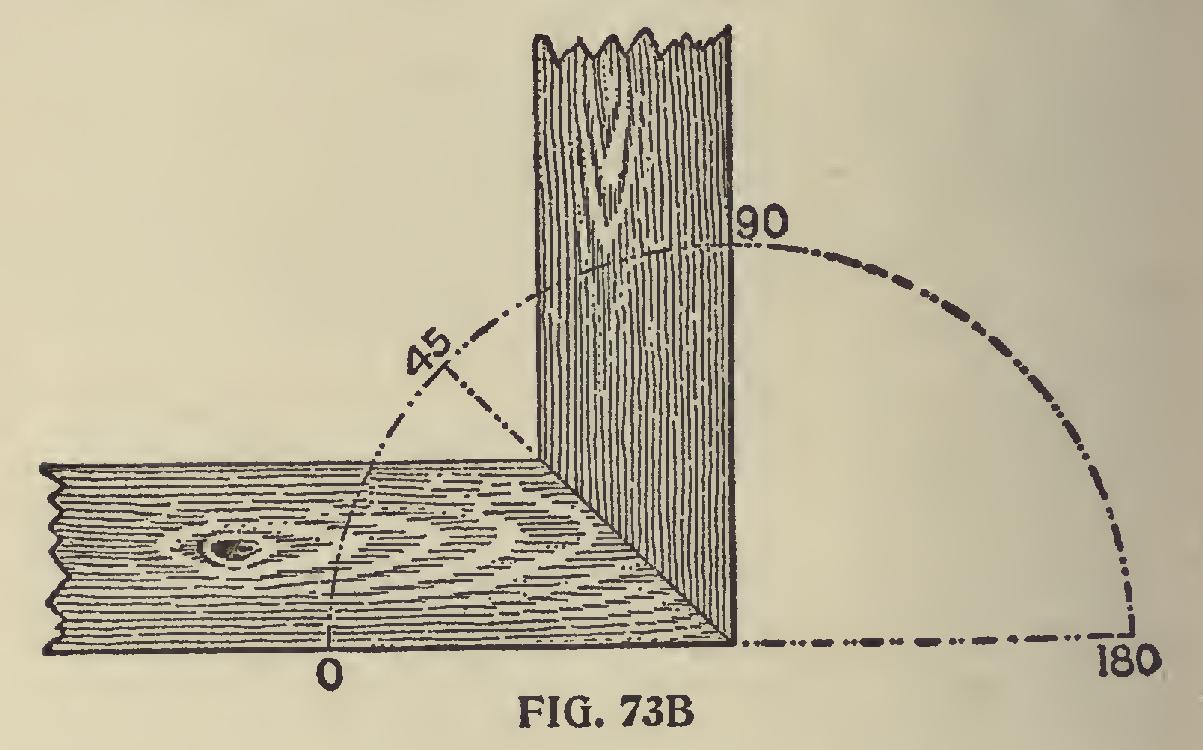
The casual observer sees nothing in the square beyond a simple measuring tool, or for squaring off the end of a board, which is the simplest of all the movements of the square. Yet as simple as it is, it is governed by the degrees, as will be shown in referring to Fig. 73a.

In all cases a straight line, which may be the edge of a timber, represents one side of an angle from which the other side of the desired angle is reckoned, and in reality represents 180 degrees. Now, since the arms of the square set at an angle of 90 degrees with each other, just that much will it take from 180 degrees having the angle stand at 90 degrees as shown.

In Fig. 73b is shown the simplest of all miters, and it is used more than all others. The knowing ones give the definition of the word miter as, "Joining two timbers at an angle of 45 degrees," without reference to any other angle. This is contrary to general belief and we see no reason why it does not apply equally as well to any other angle, and will treat them as such, but dividing them into two classes, of regular and irregular miters. The former applies to polygonal corners, where the line of juncture is midway between the outer edge of the timbers, as shown in Fig. 73b, and the latter to corners where the line of juncture does not rest midway between the outer edge of the timbers, as shown in the lower left hand corner in Fig. 73c.

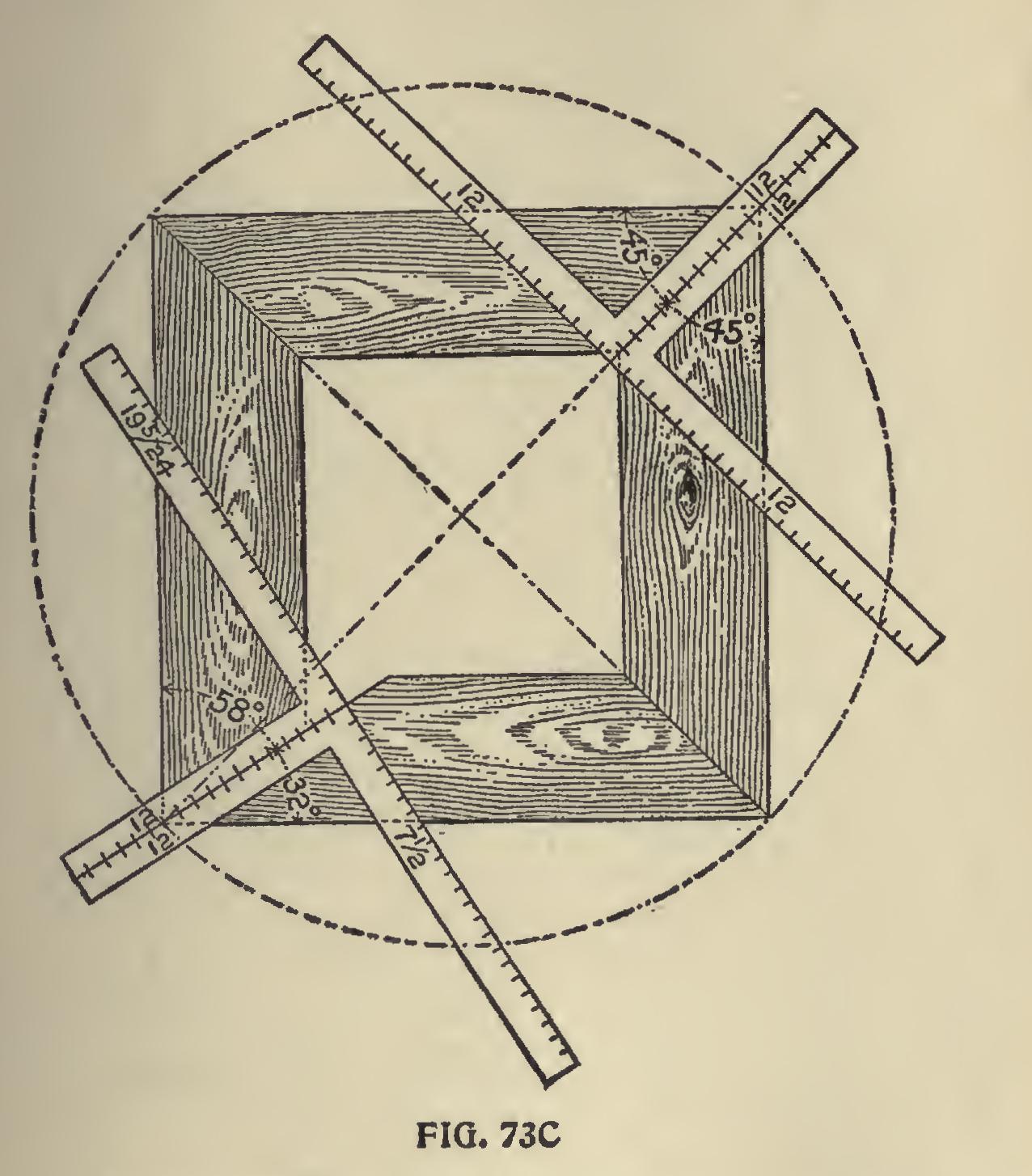
In this illustration we show both the regular and irregular miters for a square cornered frame, though it could be any polygonal corner. In this it will be seen that the *regular miter is at 12 and 12 on the squares, and at 45 and 45 degrees from the edge of the timbers. In the irregular, the angle is at 58 and 32 degrees from the edge of the timbers, and on one of the squares it is at 12 and 19 5-24, and 12 and 7i on the other, but either of the squares gives the same result as far as the miter is concerned.

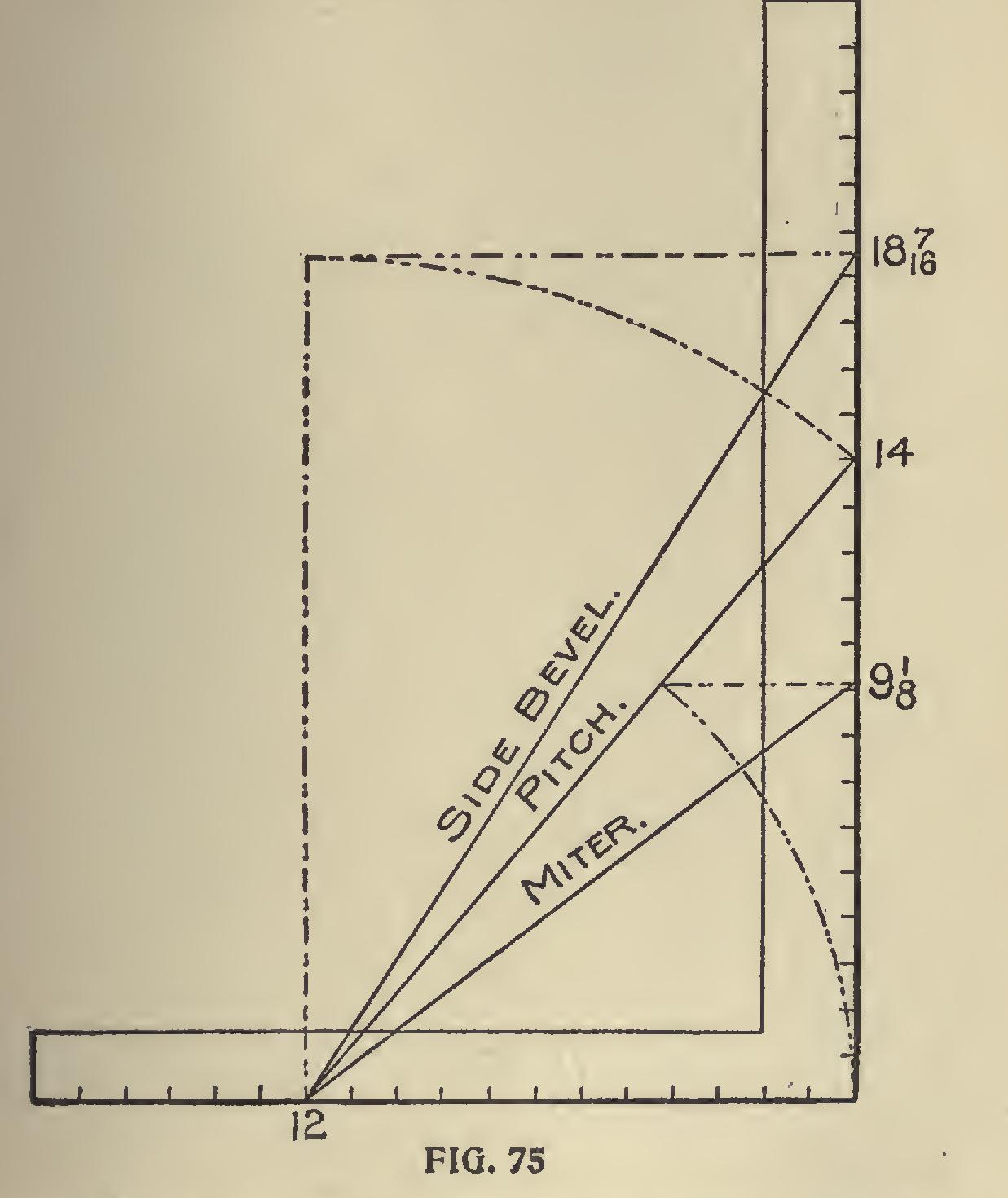
The following is another article by Mr. Woods on bevels and hopper cuts generally, which owing to its excellency, we have thought worthy of a place in this work. The author starts out by saying: If there was no given pitch, then the sides would be vertical. Now with 12 on the tongue as center, draw arc of same radius from the heel to a point directly above and square over the blade; 12 and 12 will give the miter, Fig. 74. Simple enough, but do you know that

this simple rule applies when there is a pitch given? At the point where the arc intersects the pitch taken on the blade will give the miter, the blade giving the cut. See Fig. 75. For the side bevel across the board, transfer the length of the pitch to the blade, the tongue giving the cut. These figures also give the side cut of the jacks for a roof of same pitch. The blade in this case giving the cut.

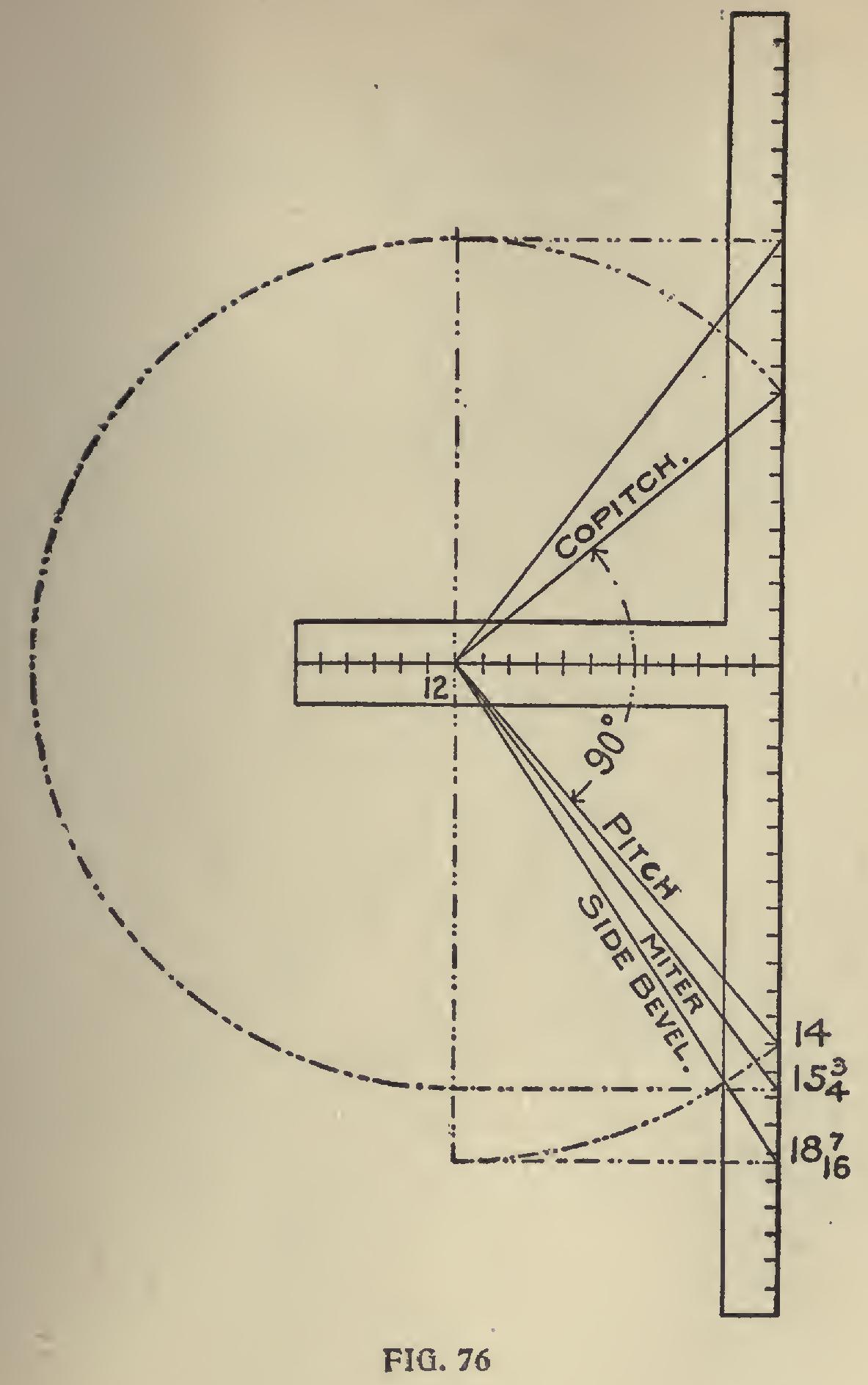
Now we will give another method of finding the miter. In all roofs and hoppers there is an unseen pitch which we will call co-pitch. Assum ing that the edges of our board are square the co-pitch would stand at an angle of 90 degrees with the given pitch. See Fig. 76.

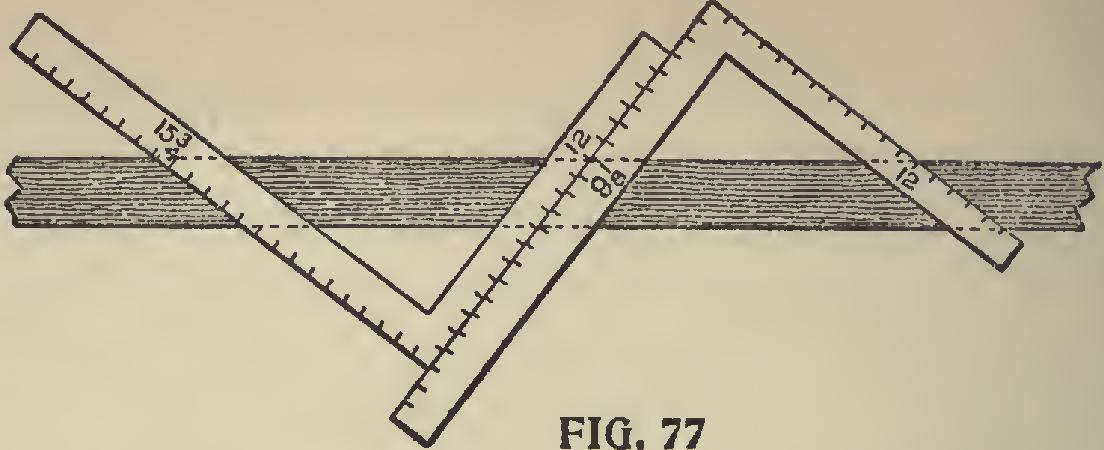
The rule given in Fig. 75 for the side bevel will apply to the miter, but instead of using the length of the given pitch substitute that of the co-pitch, and by referring to Fig. 76 we find this to be 154 inches on the blade. Now for proof, see Fig. 77. Twelve and 9i first method, and 12 and 154 second method. The blade giving the cut in the former, and the tongue in the latter.

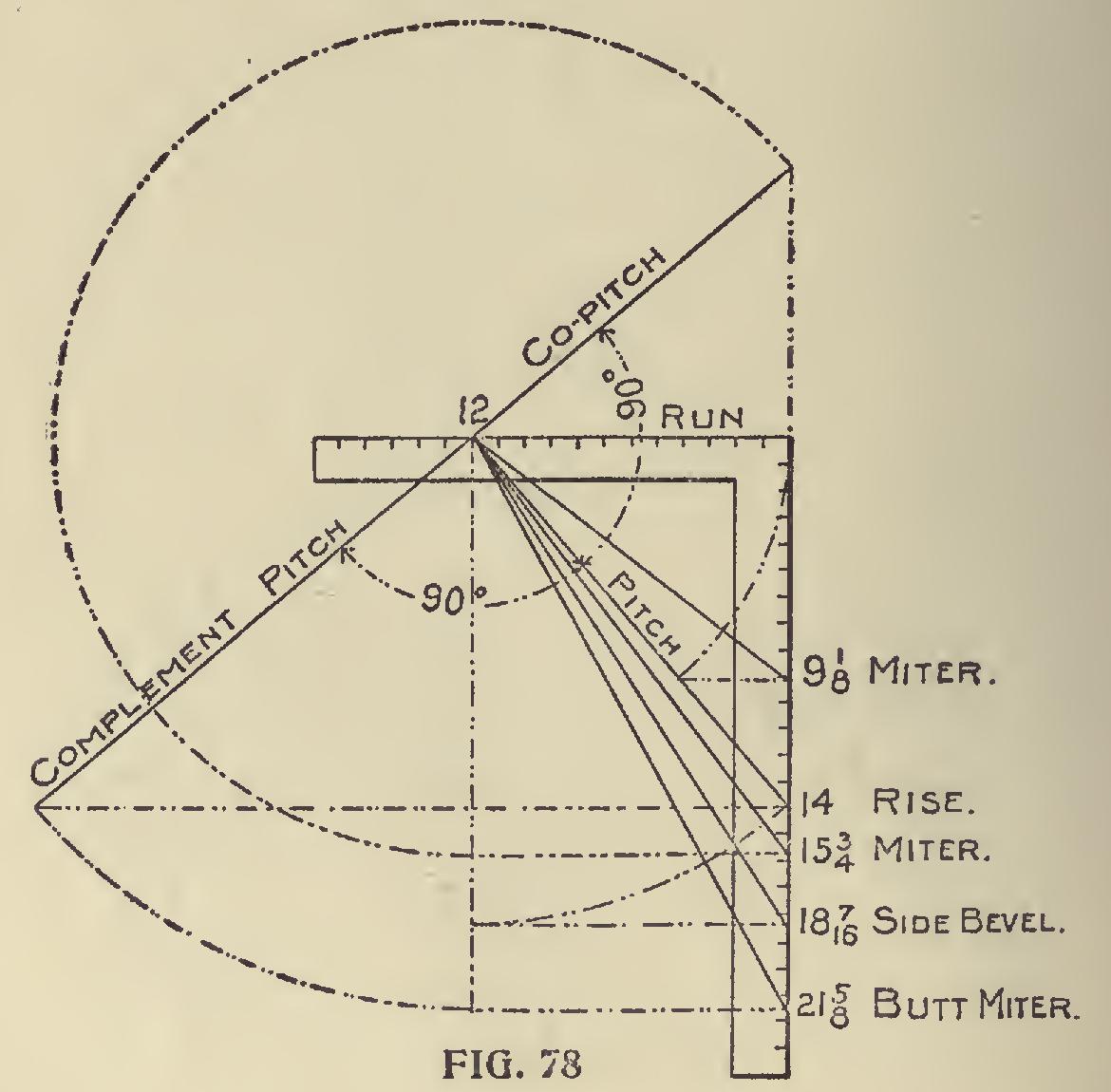
In Fig. 78 is shown all that is contained in the other figures, besides showing another pitch. It is an extension of the co-pitch to a point of the given pitch. This we will call complement pitch. The length of this pitch transferred to the blade will give the butt-joint or miter: the tongue giving the cut.

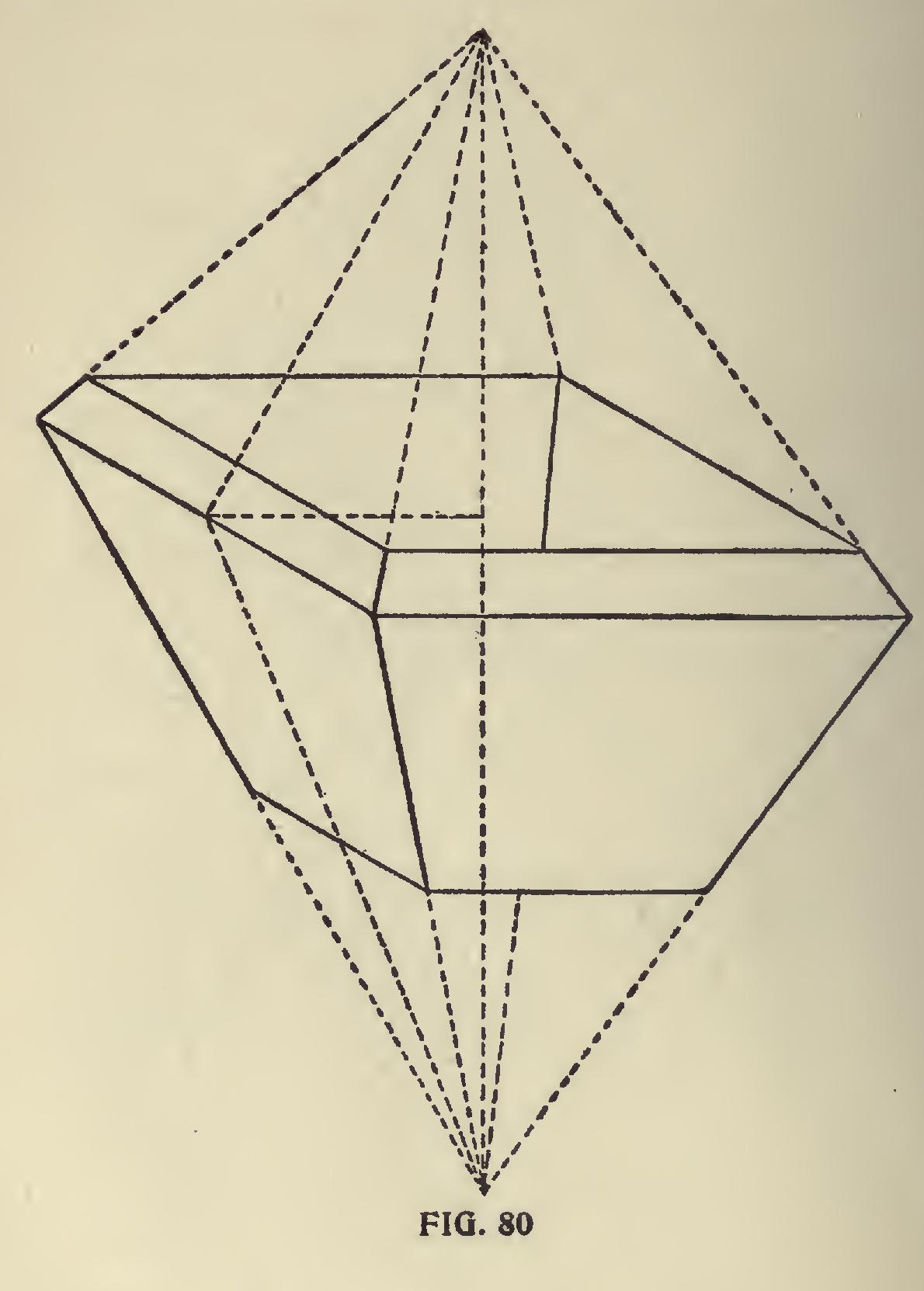
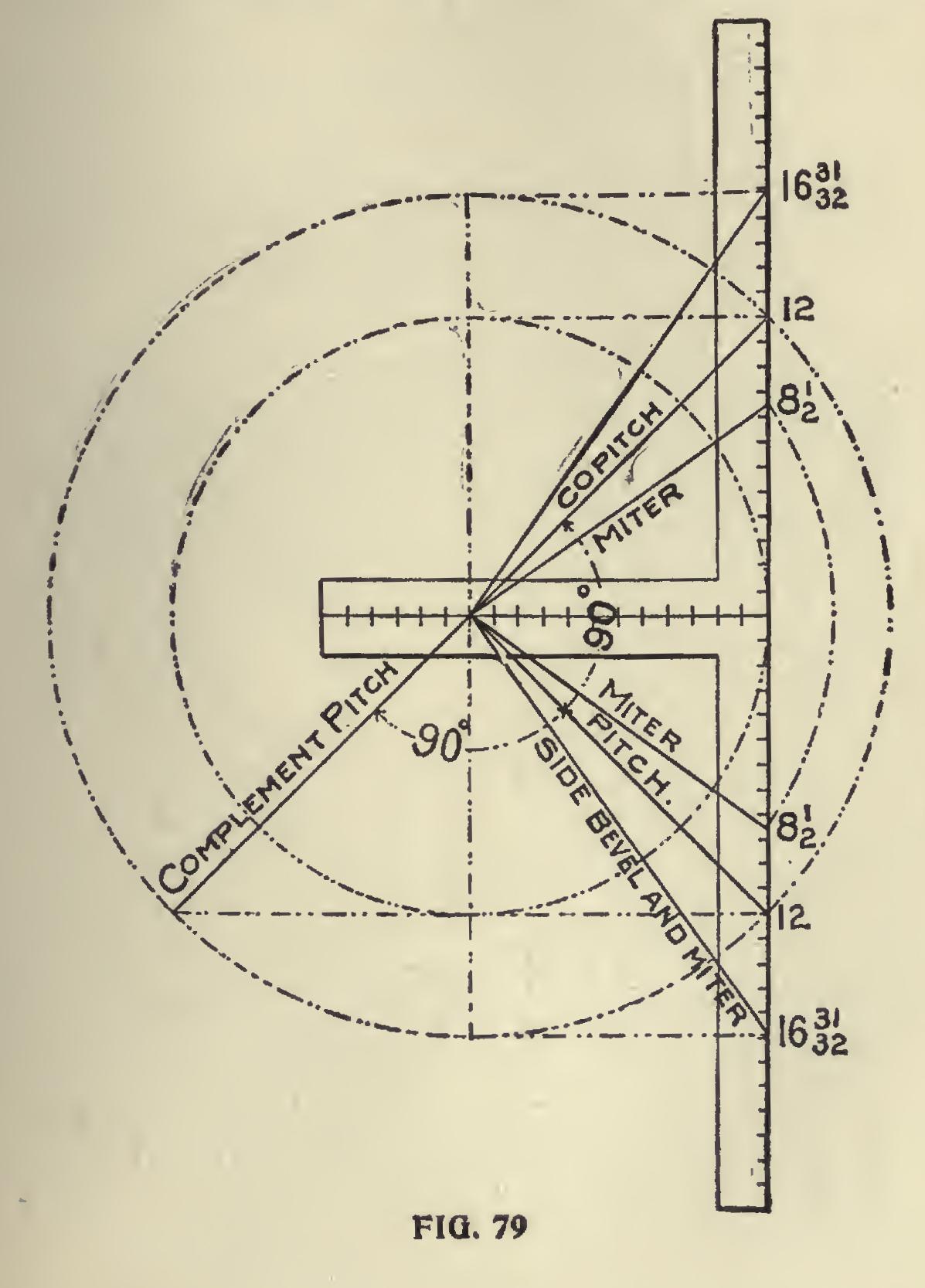
In Fig. 79 is shown a diagram for a hopper of one-half pitch. In this all of the pitches are of equal length, therefore 12 and 16 and thirty one-thirty-seconds will give all of the cuts; the tongue giving the cuts in each case. Fig. 80 and 81 are simply fillers and self-explanatory.

From the foregoing it will be seen that the standard of measurement is 12 on the tongue of the square, and this applies to any run or flare given the hopper. The preceding illustrations apply only to the square cornered hopper, but the rule therein used applies to any regular polygonal hopper. For example we will take the pentagon or five sided hopper, and in this we will show two methods of obtaining the miter bevel.