Stair Building

Another excellent method for obtaining the section of a raking mould that will intersect a given horizontal moulding, is given below, also the manner of finding the cuts for a miter box for same. The principles on which the method is based being, first, that similar points on the rake and horizontal parts of a cornice are equally distant from vertical planes represented by the walls of a building; and, second, that such similar points are equally distant from the plane of the roof. Representing the wall faces of a building by the line DB (Fig. 111), and a section of the horizontal cornice by DBabcdef, Bab being the angle of the roof pitch; draw lines aa", cc", ff", parallel to DB and intersecting the line ka", which is drawn at right angles to DB through the point B; then, with B as a centre, describe the arcs a"k, c"1", etc., intersecting the same line ka" on the opposite side of DB; after which extend lines from the points r"1"k, parallel to DB. This gives the point k at the same distance from DB as the points a and a", and the line 11" at the same distance as cc". The rest of the same group of parallel lines are found to be simi larly situated with respect to DB.

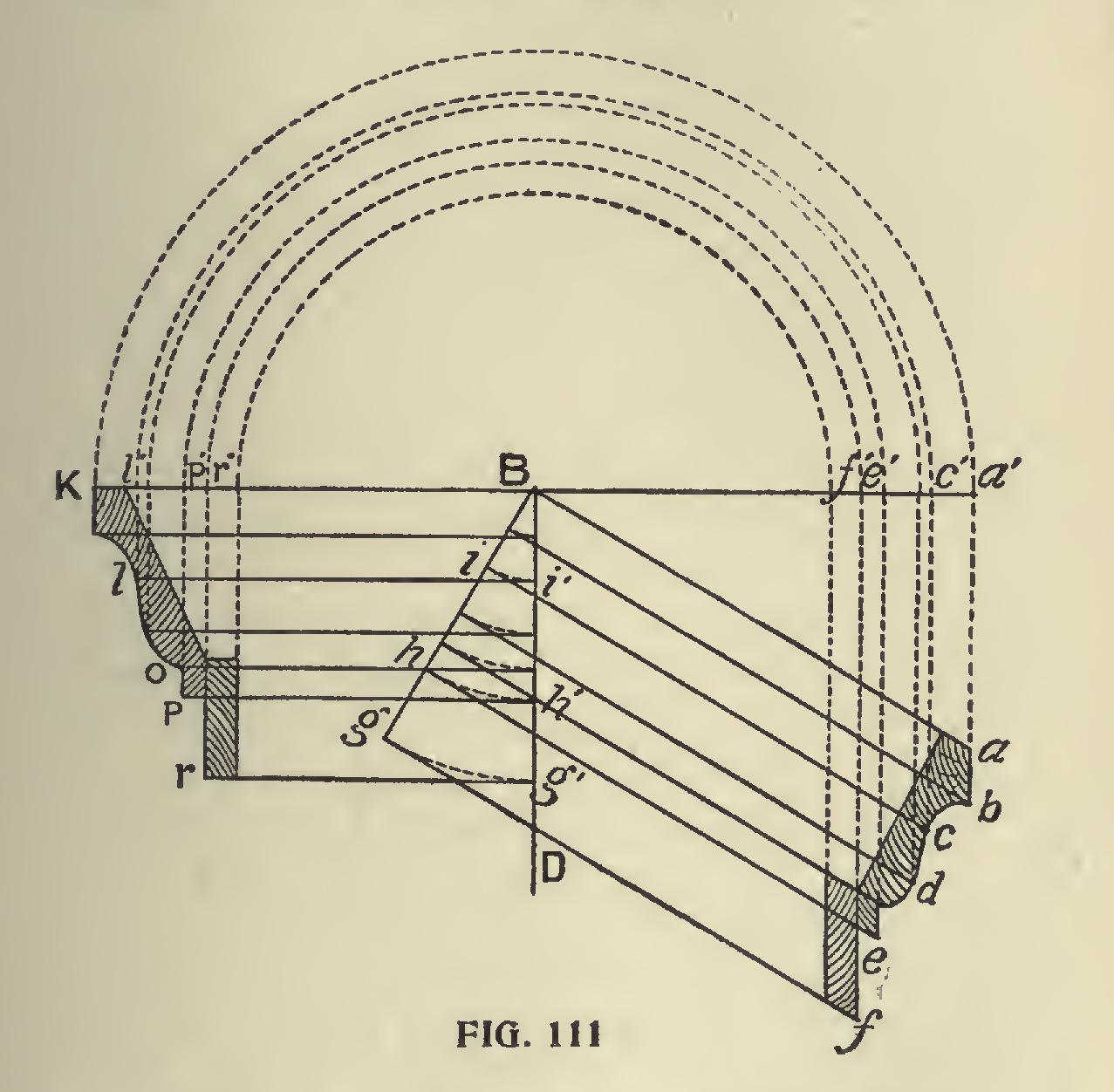
From Descriptive Geometry we have the prin ciple, that if we have given two intersecting lines contained in a plane, we know the position of that plane; hence we may represent the plane of a roof by the line Ba and Bk (Figs. 111 and 112); and since it will be most convenient to measure the distances required in a direction perpendicular to that plane, in following out the principle draw lines from the points cef, etc., parallel to Ba and intersecting the line Bg, which is made perpendicular to Ba. This gives us on Bg the perpendicular distance of the points cef, etc., from the line Ba. From the intersections

of these lines with Bg, and with B as a center, describe arcs intersecting the line DB at i", h", g", etc.; from these intersections with DB draw lines i"1, h"p, g"r, etc., parallel to Bk, until they intersect the first group of lines drawn from the same point on the horizontal section which will give the similar point of the rake section. Taking the point 1, for example, we have, as before proved, 1 at the same distance from DB as c, and i being at the same distance from Ba as c, Bi being equal to Bi", and Bi" equal to 11", 11" is equal to Bi", and consequently, 1 is the same distance from Bk as c is from Ba, which is in accordance with principle already shown. The intersection of each set of lines being found and marked by a point, the contour of the moulding may be sketched in, and the rake moulding, of which the section is thus found, will intersect the given horizontal moulding, if proper care has been taken in executing the diagram.

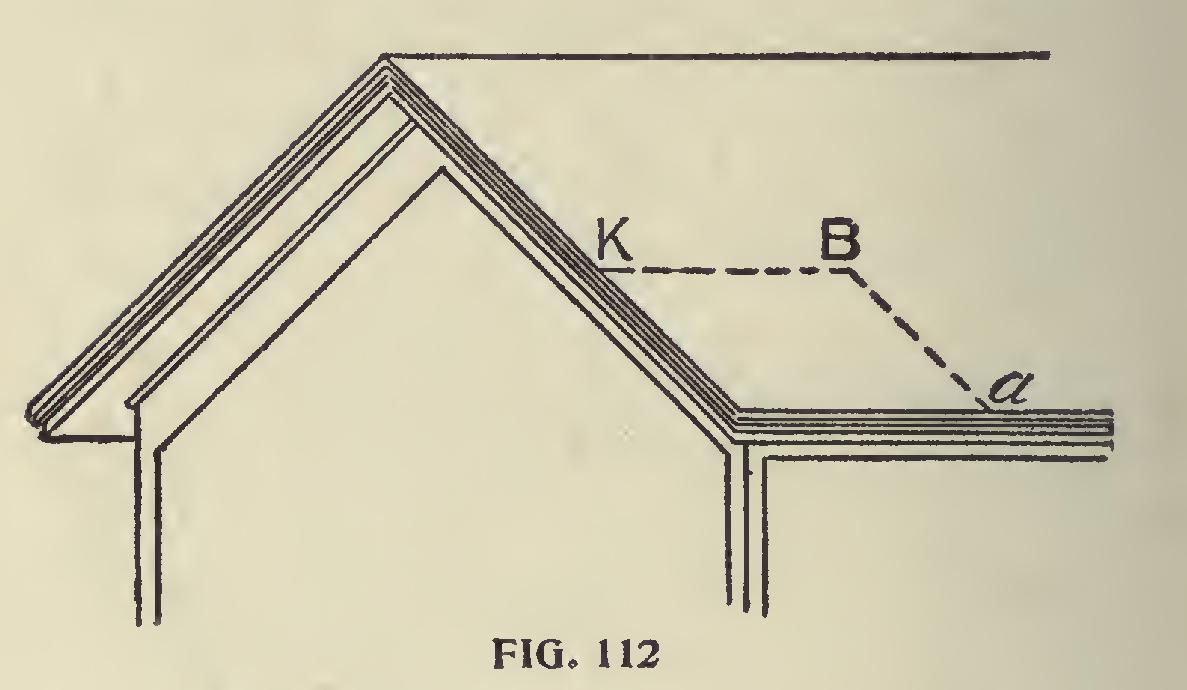
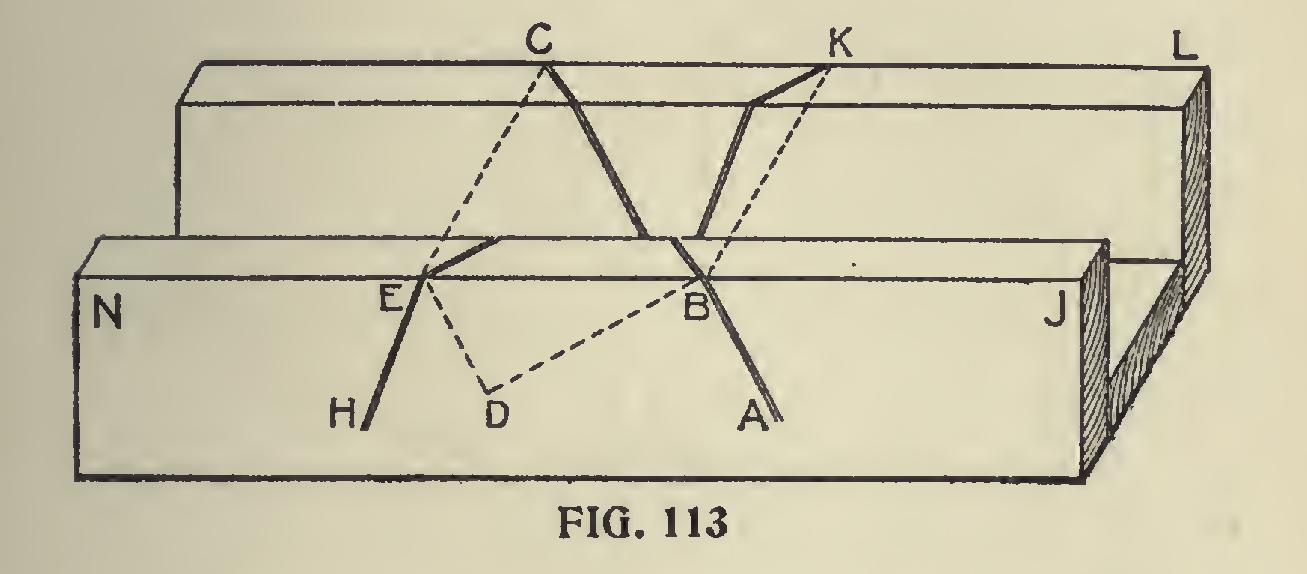
Fig. 113 shows how to find the miter cut for the rake moulding, the cut for the horizontal one being the same as for any ordinary moulding.

Take an ordinary plain miter box, NJL, and draw the line AB, making the angle ABJ equal to the pitch angle of the roof. Draw BD per pendicular to AB, and extend lines from B and E square across the box to K and C; join BC and EK. ABC will be the miter cut for two of the rake angles; HEK will be the cut for the other two anglesTthe angle HEN being equal to the angle ABJ. In mitering, both horizontal and rake moulding, that part of the moulding which is vertical when in its place on the cornice, must be placed against the side of the box.