Intersection and Development 75

86. In Fig. 68 is shown a right circular cone standing on its base, and intersected by a plane X, which is at right angles with V. The base may be divided into any number of parts—in this case twelve—and the elements of the cone drawn, as 0-1, 0-2, 0-3, etc. These elements are cut by the plane in points showing in elevation as a, b, c, etc., and these points are then pro jected to corresponding elements in plan.

The points d and m are located in the plan as follows: Pass a plane Z through the points d and m, and parallel to the base of the cone. Then Z will cut the cone in a circle whose diam ter is x-y; and this circle, lying on the surface of the cone, will evidently pass through the d and m. The circle x-y is drawn in plan, and, by its intersection with the elements 04 and 040. fixes the position of the points d and m. A smooth curve drawn in plan through the points a, b, c, d, etc.. is the projection of the re quired intersection. The section is an ellipse, and its real size and shape are not in plan.

We shall now proceed to the development of the cone and the section cut by plane X. The cone may be supposed to be placed with its vertex at 0'. and the element 0-1 at 0'-1'; the cone is then rolled until all of the curved surface has come into contact with the paper. As the cone rolls on the plane. the various elements will take positions such as o'-2', 0'-3',---0'-6' to 0'4", and the edge of the base will develop into the curve passing through the points 1', 2', 3', 1". As all of the elements of the cone are the same length, the points 1', 2', 3', etc., will all be at the same distance from 0'; that is, they will lie on the arc of a circle struck from 0' as center. The radius of the circle is the true length of any element of the cone, as shown by 0-1 in eleva tion. The positions of the points 2', 3', etc., are found by taking in the dividers the distance be tween any two consecutive points of the base as seen on H, and laying this off from 1' twelve times. Lines joining these points with 0' will represent the positions of the elements in development.

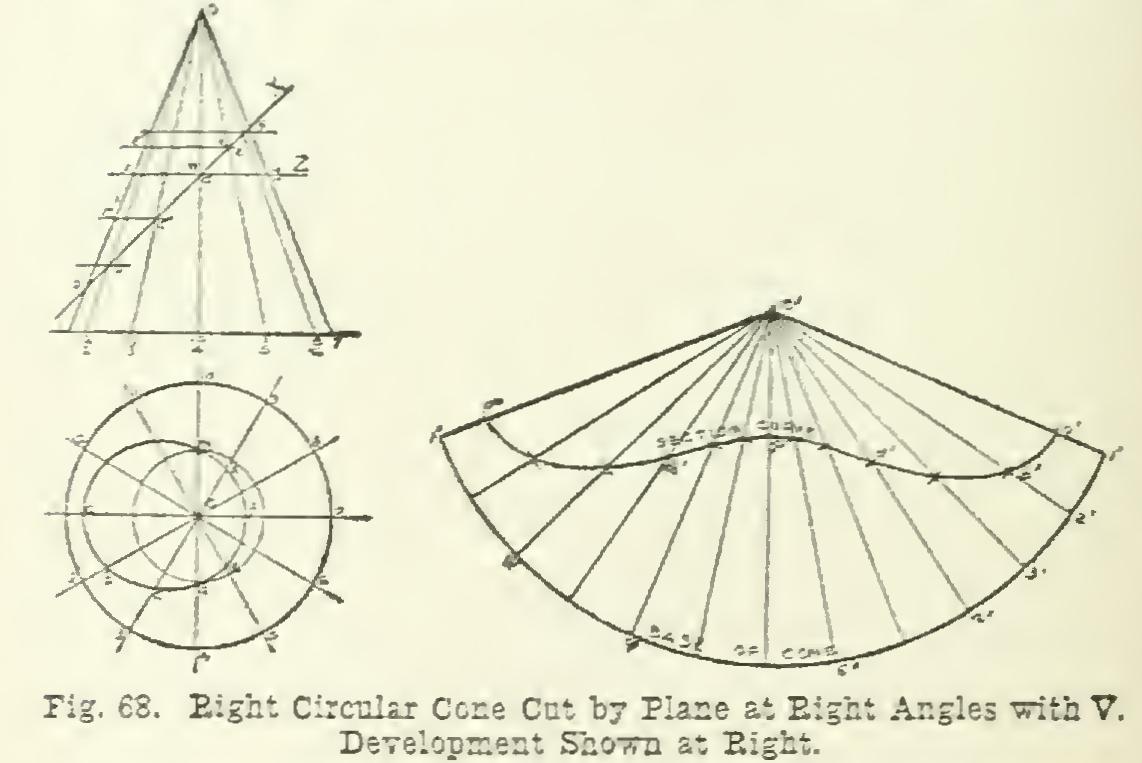
As regards the development of the section cut by plane X, the different points of the curve may be found on the elements by laying off from 0' the true distance from the points of intersec tion to the vertex 0. The distance 0-a in ele vation is a true length, since 0-1 is parallel to V (Article 73, e). The point a' is then located at

once. The true distance of the other points from the apex may be found by projecting hori zontally from the points in elevation to 0-1, on which line their true distances from 0 are shown. These distances are then laid off from 0' on the respective elements; and a smooth curve drawn through the points will be the section curve required.

Attention is called to the fact that the length of the developed base 1', 2', 3',--6'-1" is not exact, since, in the first place, it is impossible with the dividers to measure exactly the length of a curve; and in the second place, because it is likewise impossible to apply exactly with the dividers any given distance along a curve. It should be said, however, that by taking points sufficiently close together a very good approx imation indeed can be obtained.

87. Fig. 69 shows an example of a cone stand ing on its base and intersected by a plane Y perpendicular to H.

Elements of the cone are drawn as before, except that it is unnecessary to draw any on the further side of the cone. In plan, the elements are seen to intersect plane Y in points a, b, c, d, and e, which are then projected to the elevation onto the corresponding elements. It will be noticed that in elevation the points a and b are quite a considerable distance apart; so two more elements are drawn in plan, one between 0-2 and 0-3, and one between 0-5 and 0-6. These ele ments determine two more points on the curve. The highest point c cannot be found in elevation by direct projection, but is located by a special construction.

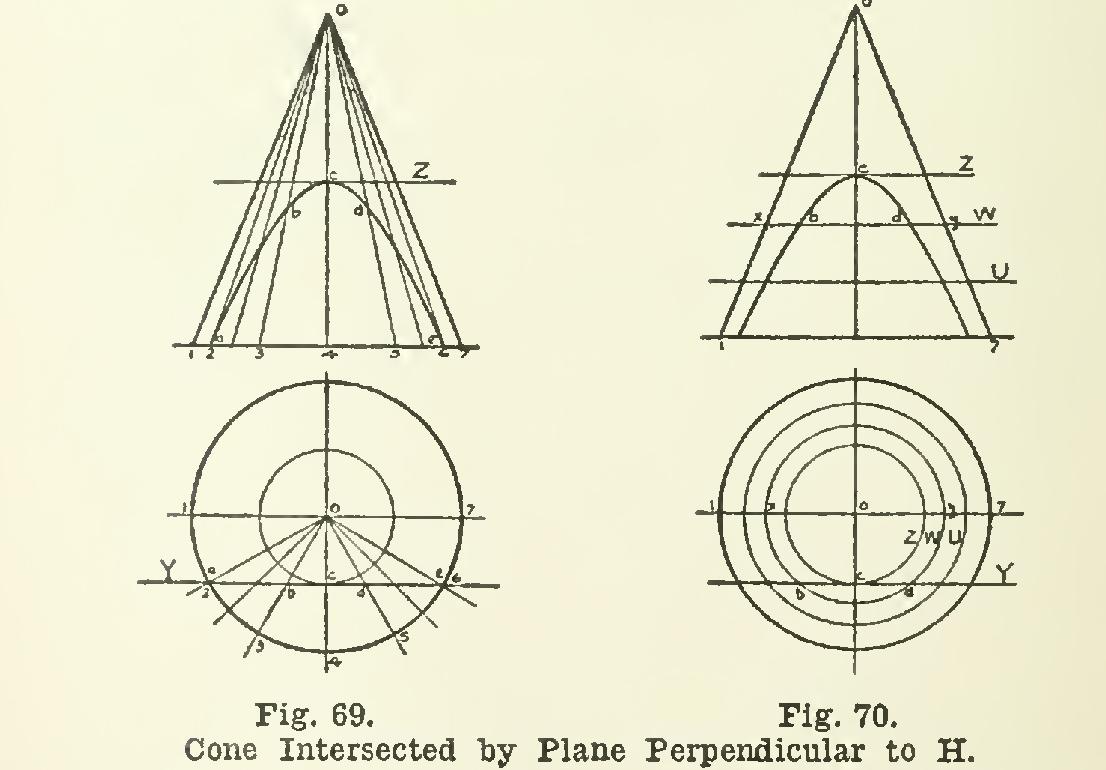
A circle with center 0 is drawn on the plan passing through c. Considering this circle as lying on the surface of the cone, it will intersect all of the elements, and will lie in a plane parallel to the base. For convenience, the points in which the circle intersects the two outside elements, 0-1 and 0-7, are used, and projected to 0-1 and 0-7 in elevation; then the plane Z is the plane containing the circle, and c in eleva tion is where Z cuts element 0-4. This section curve is shown in its true size and shape in ele vation, and is known as a hyperbola., this name being given to the curve cut from any cone by a plane parallel to the axis.