Intersection and Development 75

The development of the section curve is obtained by locating the points a, b, c, etc., in the development on their respective elements, and at the true distance from the foot of the element. These distances are all shown in the elevation, and consequently may be transferred at once to the development; and a smooth curve drawn through a', b',...e'. ..n'. . . a" will be the developed curve.

Intersection of Solids 92. Points on the intersection of solids— that is, on the intersection of their surfaces— are the points in which lines of either surface intersect the other.

93. Visibility of the Lines of Intersection. The intersection of two solids, viewed from any given direction, is in general partly visible and partly invisible. The rule for visibility is that visible parts of the intersection must always be the intersection of visible parts of each sur face. Thus the intersection of the upper parts of two surfaces would be visible in plan; while the intersection of the upper side of one with the under side of the other would not be visible.

94. Intersection of Solids Bounded by Plane Surfaces. When one solid of this el ass—as. for example, a pyramid—intersects another pyra mid or prism, the intersection will consist of one or two figures bounded by straight lines. Points on such an intersection may be deter mined by finding where the edges of either solid intersect or pass into the faces of the other.

95. A square prism standing on its base, is intersected by a triangular prism with its axis parallel to both V and II, Fig. 73. The end view at the right shows the left-hand end of the horizontal prism. The points in which the edges of the triangular prism intersect the faces of the other prism, will be shown at once in plan, since in plan the surfaces of the square prism are seen edgewise. The edge 3-4 inter sects the face adef at a point seen in plan as and the V projection my is found in eleva tion on 3Y-4v.

Similarly, edge 2-6 cuts the same side adef at point n. Then the line m-n is the intersection of one side 2-3-4-6 of the triangular prism with the side of the square prism. In elevation, will be a visible line (Article 93).

The next edge, 1-5, evidently does not inter sect the face adef, but cuts the adjoining side abgf. The face 1-2-6-5 must then cut both faces

of the other prism in a broken line, running from point n to the point in which the face 1-2-6-5 cuts the edge a-f, and continuing from this point to point q on the face abgf. The point where the plane 1-2-6-5 cuts the edge is found in the end view. In the end view, a part of the edge is shown as the T-square line aP-x. The plane 1-2-6-5 is seen edgewise in line 1P-2P, and cuts aP-x at point o.

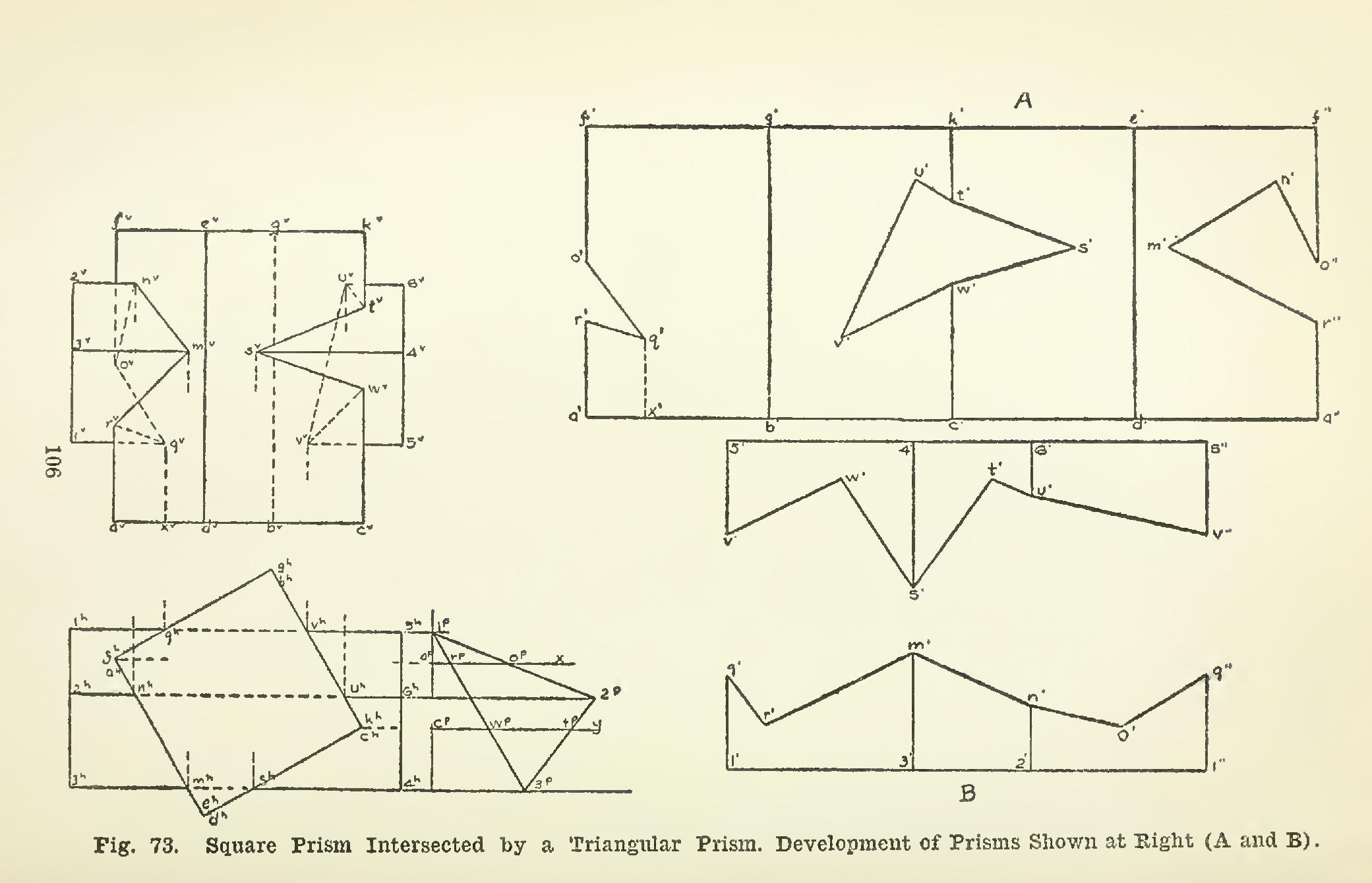
The point 0 on edge a-f is at a distance higher than the edge 1-5; hence the length aP-oP is laid off in elevation above 1-5, locating o°. The intersection of face 1-2-6-5 is the broken line In a similar way, the under side 1-3-4-5 breaks around the edge a-f, the point r also being located from the end view. The figure mnoqrm is the intersection of the tri angular prism with the left-hand sides of the vertical prism.

By the same method, the intersection on the two right-hand faces is found to be the figure stuvw. The visibility of the intersection and of the edges of the solids, should be studied until perfectly understood.

Development of the Prism. The square prism is shown developed at A, Fig. 73 (the ends are not shown in the development). The four sides of the prism are equal rectangles whose length is shown in elevation, and width in plan. Beginning with face abgf, the devel oped faces of the prism will appear as the four equal rectangles shown in the figure.

Location of the Intersection on the Develop ment. Beginning with face abgf, the points r and 0, which fall on the edge are located at the same distance from a as in elevation. The point q is at a perpendicular distance from the edge and at a distance above equal to the height xv-qv as shown in elevation. The point q' is then located by means of these two distances, and then joined with o' and r'.

Next consider the intersection tuvw on the face bckg. Points t and w are located at once on the edge c'-k' at t' and w'; and u and v are determined in position at If and v' in the same way as for point q.

It is essential to note that the distance of if and v' from the edge c'-k' must be taken from the plan, and not from the elevation. The figure t'u'v'w' is the developed intersection on this face.