Intersection and Development 75

For the next face, cdek, the points t' and w' are already found, and s' may be determined as already explained. On the face dafe, the intersection develops as shown at o"n'm'r".

Development of the Triangular Prism. The triangular prism is developed at B, in the same figure. The method is similar to the preceding one, the distances of the points from the end of the prism being measured in either the plan or the elevation, and the distance from the long edges measured on the end view of the prism. The corresponding points have been lettered the same in both developments.

96. Intersection of a Prism with a Pyramid. In Fig. 74 is shown a rectangular prism inter secting a square pyramid. The pyramid stands on its base, and the prism has its edges but not its faces parallel to the H plane.

In this case, none of the sides of either solid are seen edgewise in either plan or elevation; hence another view is necessary. This view, drawn at X, is taken in the direction of the arrow so as to show the prism endwise; for in this position the faces of the prism are seen edgewise as straight lines, and the intersection may be determined in part as in the pre ceding case.

In the projection X, the base of the pyramid is at right angles to the direction of the view that is perpendicular to the edges of the prism, and the height of the pyramid is the same as in elevation.

In this example, the edges of the pyramid and prism have been lettered with capitals, and the points when found have been numbered. The plan will be adopted of beginning at some point, and tracing the intersection around in the same direction until completed.

Starting with the edge A of the pyramid, it is found in view X to intersect face FE of the prism at point 1, and lh and r are located. Next, B cuts the same face FE in point 2, and 1 and 2 are joined in plan and elevation, the line 1-2 being visible in plan and invisible in eleva tion. The next edge of the pyramid, C, does not cut the face FE. There must, however, be an intersection of FE with the side BC of the pyramid, since FE cuts the edge B at 2.

Let it be imagined for a moment that face FE is extended in width so that C cuts it at m, then a line joining 2 and m would be the intersection of FE with side BC of the pyramid.

The imagined widening of FE would not alter the direction of the intersection, but only the length, so the portion 2-3 of 2-m is the actual intersection wanted.

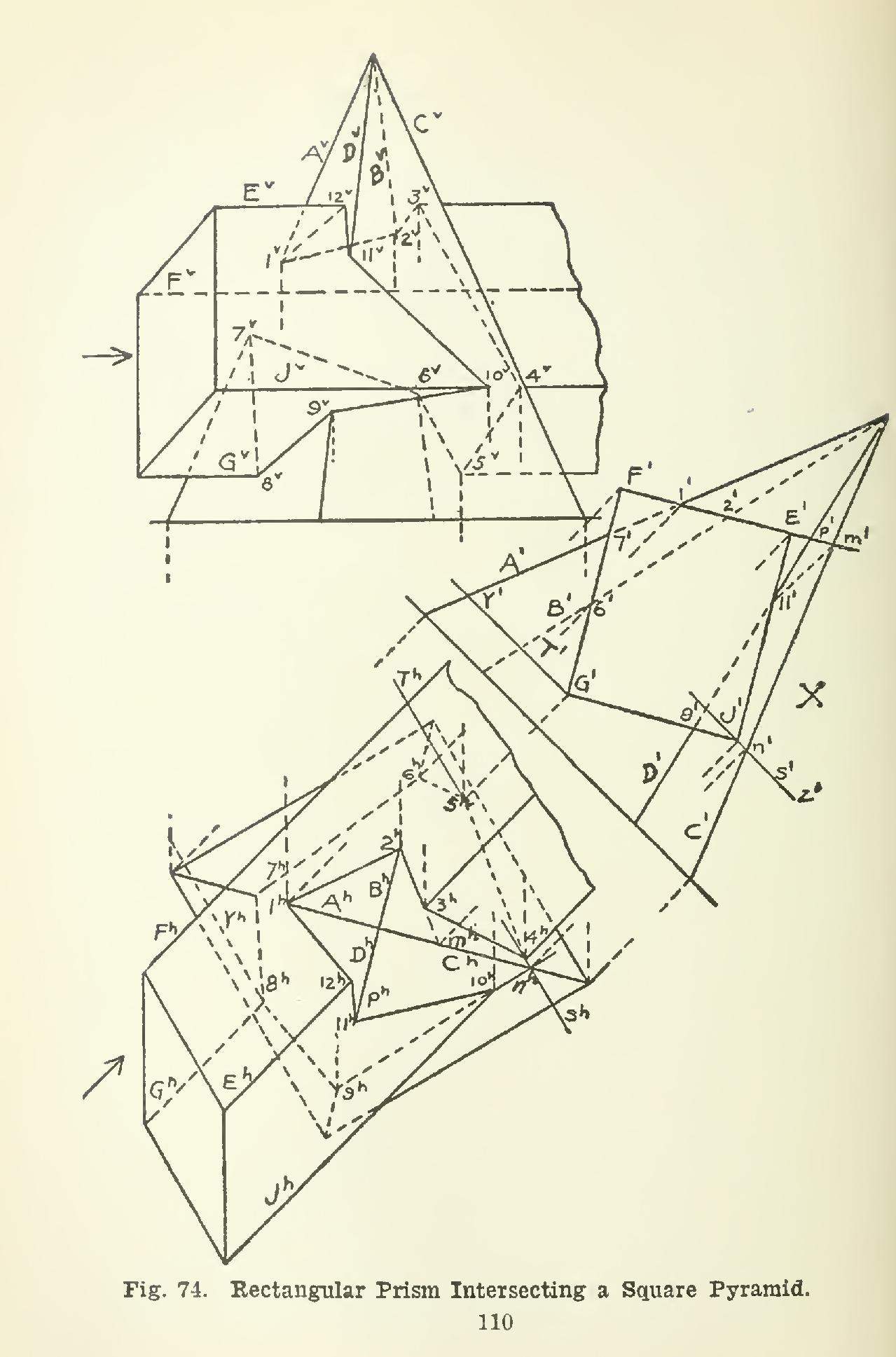
It should also be noted that point 3 is where edge E intersects the face BC of the pyramid. The intersection is continued on BC by the intersection of face EJ of the prism, running from 3 to where J cuts the face BC. This point on J is found in this way: If a plane parallel to the base be passed through J, it will cut the pyramid in a square parallel to the base (Arti cle 79); and one corner of the parallel square is shown in view X as n' on C'; and line S on face BC, and parallel to the edge of the base, is one side of the square. The edge J intersects line S (see view X), and, as line S is on face BC of the pyramid, this point (4) is where J cuts the face of the pyramid. Point 4 is then connected with 3.

Similarly, by the use of line T, edge G is found to pierce the face BC at point 5, which is the next point of the intersection. The remainder of the intersection is found in the same way. The visibility in plan and elevation is determined as previously explained (Article 93).

In

projecting the points from the plan to the elevation onto the edges B and D, it is diffi cult to determine the exact V projections, owing to the steep slope of B and D. • The position of the points in elevation, however, may be tested by observing that in view X the perpendicular distance of any point from the base is simply the height of the point, and the height of the point in elevation should be the same.

97. Intersection of a Cylinder with a Prism. Fig. 75 represents the intersection of a circular cylinder and an irregular four-sided prism. The two are placed in the first angle, the prism standing on its base and the axis of the cylinder parallel to both V and H.

The intersection in this case will consist of three curved lines, one on face .AB, one on BC, and the third on CD. The cylinder may be con sidered as piercing the prism, and points will be found in which lines on the cylinder intersect the faces of the prism.