Intersection and Development 75

Development of the Cylinder.

Beginning with the element L, which passes through point 10, and placing 10 at the outline of the cylinder is developed as a rectangle, as in Fig. 72, except that, instead of making a new divi sion of the base into equal parts, the points already found are used. Thus the points 9, 8, 7, 6, etc., are taken from the end view, and spaced off at 7„ etc., in the development. The are between 1 and 10, Fig. A, is divided into three equal spaces. The right-hand end of the cylinder is made the lower side of the development.

Development of the Curve of Intersection. The points of the intersection are located sym metrically on either side of X-Y; so X-Y is drawn on the development at X'-Y', at the same distance from the end of the cylinder as in plan.

Beginning with point 1 on X'-Y', the dis tances from X-Y of the other points, 8, 7, 6, etc., are measured in the plan; and then, in the development, these distances are laid off on the corresponding elements, both above and below X'-Y', thus obtaining at once both halves of the developed intersection.

Approximate Developments 99. Of curved surfaces, it may be said in general that only those can be truly developed which contain straight lines on their surfaces, and which, in addition, when brought into con tact with a plane, will touch in only one straight line.

100. It is possible, however, to construct for non-developable surfaces one or more figures which will have nearly the same total area as the given surface, and which, when properly joined and bent or curved, may be made to assume nearly the shape of the original surface. Such a figure is called an approximate development.

Essential Principles of Intersection and Development 101. When a plane cuts one or more lines, an edgewise view of the plane will determine the various points of intersection.

102. If a cone, cylinder, pyramid, or prism be cut by a plane parallel to the base, the section will always be a figure parallel to the base and similar to it in shape.

103. The intersection of a plane with a curved surface is determined by means of the points in which the plane cuts lines on the sur face. These lines may be either straight or curved, according to the nature of the surface.

104. The intersection of two surfaces is determined by means of the points in which lines on either surface intersect the other.

105. For the intersection of two surfaces, the points are first found in the projection which shows an end view of one of the solids. Two such end views may be necessary.

106. A development shows the true length of any line, straight or curved, which lies on the given surface.

107. A right circular cone develops into a sector of a circle, in which the radius is equal to the length of an element of the cone.

108. A right circular cylinder with both ends parallel will develop into a rectangle, whose length is that of the cylinder and breadth is equal to the circumference of the base.

109. We shall now make some applications of the principles of intersection and develop ment to the solution of practical problems.

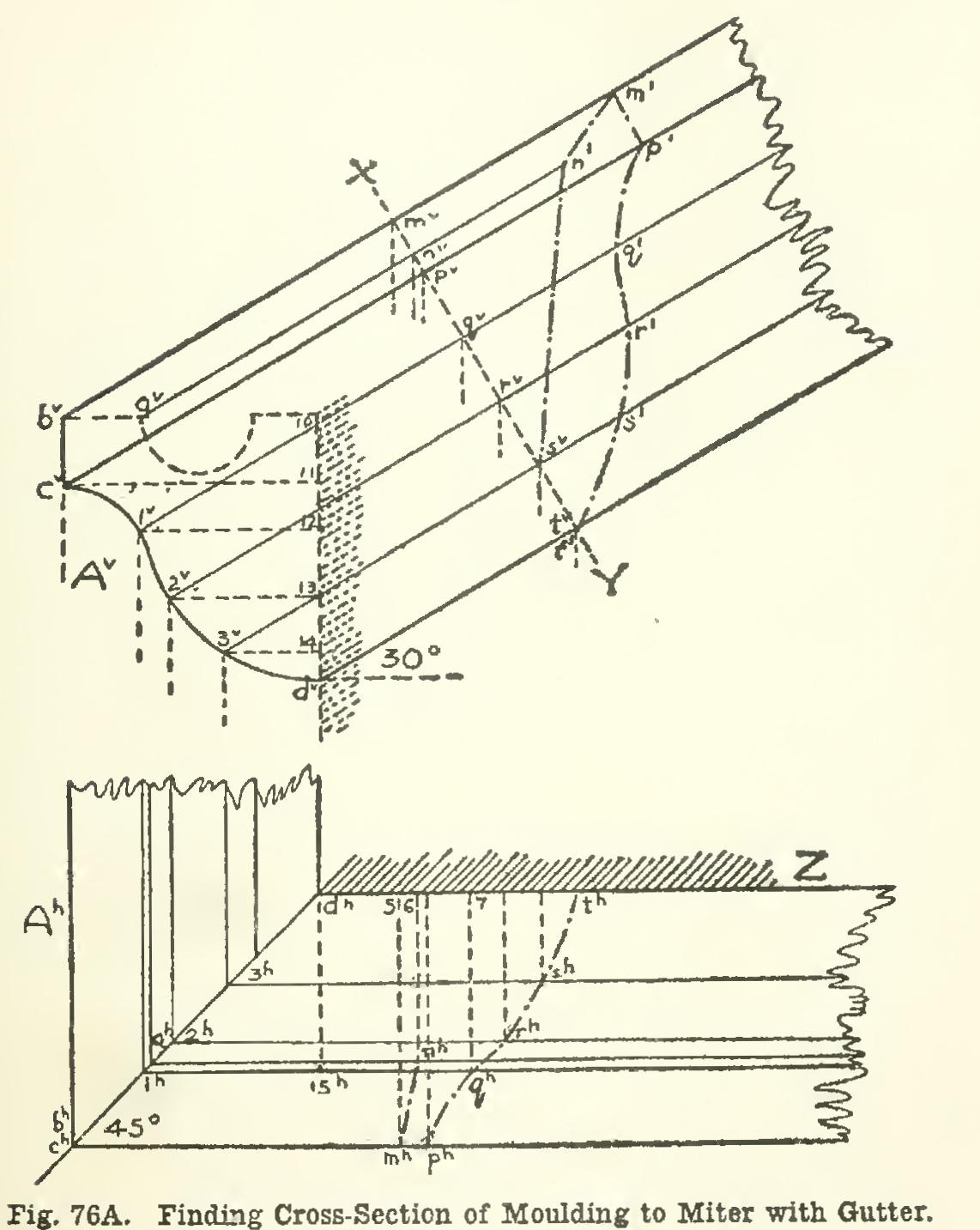
Given Cross-Section of Gutter, and Pitch of Roof, to Find Cross-Section of Rake Moulding which will Miter with Gutter Let the cross-section of the gutter be as shown in A°, Fig. 76A, and let the slope of the roof be 30 degrees. The angle of miter, as given in the plan, is 45 degrees. Lines drawn from av, bv, c°, and cr, parallel to the pitch of the roof, will represent edges of the raking mould ing, these same edges being shown in plan parallel to the V plane, which may here be con sidered as the end wall of the house.

To find the cross-section of the moulding is an application of the principles just studied. A plane cutting the moulding at right angles to its length will show the true cross-section required.

As the edges of the moulding are parallel to V, the cross-section plane will be perpen dicular to V, and will be seen edgewise on V. It may be taken at any convenient distance from the gutter, as in the position X-Y. This plane will intersect the edges drawn from a, b, etc., in the points n, m, p, and t. Since the surface between p and t is curved, it will be necessary to make use of lines drawn on the curved sur face, starting from points such as 1, 2, and 3 on the curved outline of the gutter. The plane X-Y cuts these lines at the points q, r, and s. The plan of the section cut by plane X-Y is not the true size and shape, since plane X-Y is not parallel to H (Article 54).