Miscellaneous Rules

MISCELLANEOUS RULES In connection with the work of construction, problems frequently arise that are ordinarily supposed to involve the necessity for more or less complicated mathematical computation in their solution. In the case of many of these problems, it will be found that a familiar knowl edge of the possibilities of the steel square and an intelligent use of this instrument will afford a simple and at all times available solution. Such problems are, for example, to measure a pile of lumber, to estimate the number of square yards in a job of plastering or painting, etc.

The following rules and examples have been gathered from various sources, and although they touch upon topics already treated, they are here presented with the confident belief that the reader will find among them a number of easy solutions of problems of more or less complexity that heretofore have caused him much time and trouble to work out.

Measurement.

Let us suppose that we have a pile of lumber to measure, the boards being of different widths, and say 16 feet long. We take our square and a bevel with a long blade and proceed as follows: First we set the bevel at 12 inches on the tongue of the square, because we want to find the contents of the board in feet, 12 inches being one foot; now we set the other end of the bevel blade on the 16 inch mark on the blade of the square, because the boards are 16 feet long. Now, it must be quite evident to any one who would think for a moment, that a board 1 foot wide, and 16 feet long, must contain 16 feet of lumber. Now let us take a board 11 inches wide, and 16 feet long, we just move our bevel from the 12 inch mark to the 11 inch mark, on the tongue, and look on the blade of the square for the true answer ; and so on with any width, so long as the length is 16 feet. If the stuff is two inches thick, double the answer, if three inches thick treble the answer, etc.

Now, if we have stuff 14 feet long, we simply change the bevel blade from 16 inches on the square blade, to 14 inches, keeping the other end of the bevel on the 12 inch mark, 12 inches being the constant figure on that side of the square.

To Find Number of Yards of Plastering or Painting.—If we want to find out how many yards of plastering or painting there are in a wall, it can be done by this method quite easily. Let us suppose a wall to be 12 feet high and 18 feet long, and we want to find out how many yards of plastering or painting there are in it, we set the bevel on the 9 inch mark on the tongue (we take 9 inches because 9 square feet make one square yard, (we take 18 inches, one of the dimen sions of the wall, on the blade of the square; then after screwing the bevel tight, we slide it from 9 inches to 12 inches, the latter number being the other dimension, and the answer will be found on the blade of the square. It must be

understood that 9 inches must be a constant figure when you want your answer to be in yards, and in measuring for plastering it is as well to set the other end of the bevel on the figure that cor responds with the height of the ceiling, and then there will be no movement of the bevel required further than to move it on the third dimension. This rule is a very simple and a useful one; of course openings will have to be allowed for, as this rule gives the whole measurement.

To Divide a Board Into Equal Parts.

Fig. 145 shows how to divide a board into an even number of parts, each part being equal, when the same is an unequal number of inches, or parts of an inch in width. Lay the square as shown, with the ends of the square on the edges of the board, then the points of division will be found at 6, 12, and 18, for dividing the board into four equal parts; or at 4, 8, 12, 16, and 20, if it is desired to divide the board into six equal parts. Of course the common two-foot rule will answer this purpose as well as the square, but it is not always con venient.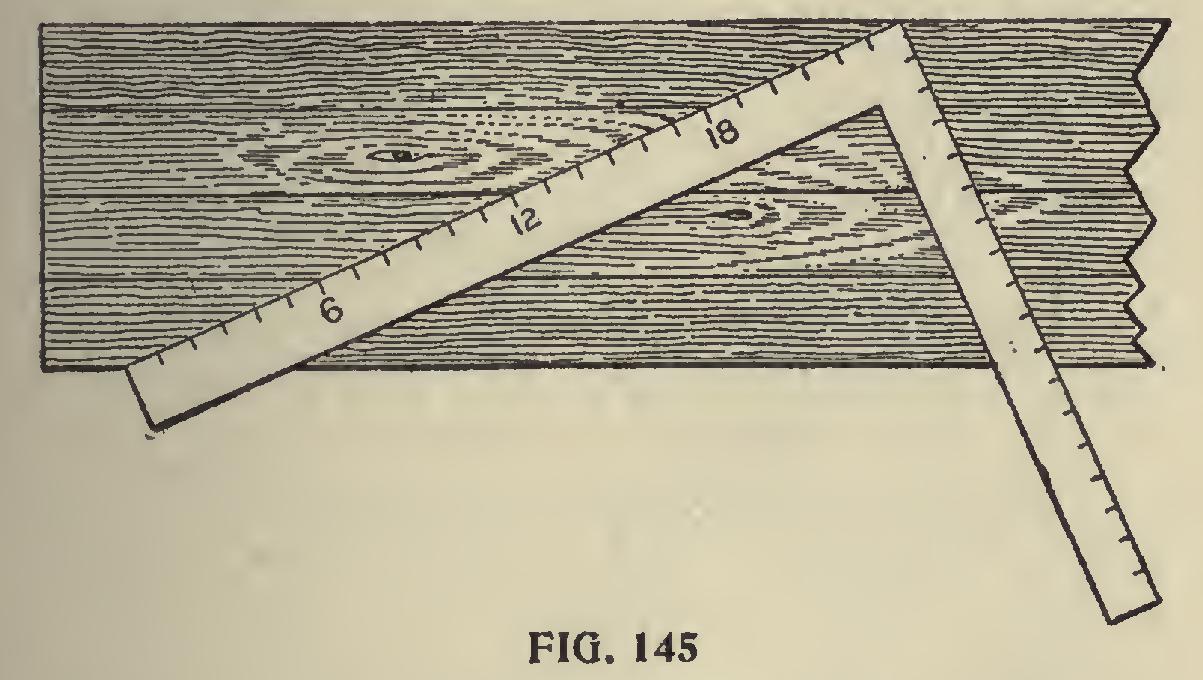

To Obtain Diagonal of Parallelogram. — If the diagonal of a parallelo gram withint he range of the square is required, it can be obtained as fol lows: Set the blade of the bevel on 81 inches on the tongue of the square, and 121 inches on the blade; securely fasten the bevel at this angle. Now, suppose the parallelogram or square as in Fig. 146 to be 11 inches on the side, then move the bevel to the 11 inch mark on the tongue of the square, and the answer, 15 and 9-16, will be found on the blade. All problems of this nature can be solved with the square and bevel as the latter is now set. There is no particular reason for using 8i- and 124, only that they are in exact proportion to 70 and 99. and 6 3-16 would do just as well, as they are in the same proportion.