Miscellaneous Rules

Let A B, in Fig. 150, be a straight line, or the straight edge of a board; then apply the square as shown, placing the 16 inch mark on the blade at C, and the 5 inch mark on the tongue at D. See that the junctions of the blade and tongue of the square with the line A B, are accurately placed, for on this depends the truth of the results. Now, suppose we wish to ascertain the circumference of a circle whose diameter is 8 inches; commencing at the point, C, we space off the diameter, 8 in ches, three times, on the line C 0, as shown at 8" 8" 8"; then square down the line 8" F, then C F will be the circumference of a circle whose diam eter is 8. It will be seen, by dotted lines in the cut, that the circumference equals the diagonal of a rectangle whose sides are respectively 24 and 7 and 15-32 inches; so that by adopting these figures (24 and 7 and 15-32), it enables the op erative to use the full length and capacity of the square. The better way however, is to work from a basis of 16 and 5, and draw the lines, C 0 and A B, to considerable length, so that they may be made available for dimensions beyond the range of the square . Now, let us suppose an instance where the circumference of a circle is wanteo: whose diameter is 10; we simply space off three tens, or thirty inches, on the line C 0, which, in this case, is at K. Square down from K to R, and C R is the length sought.

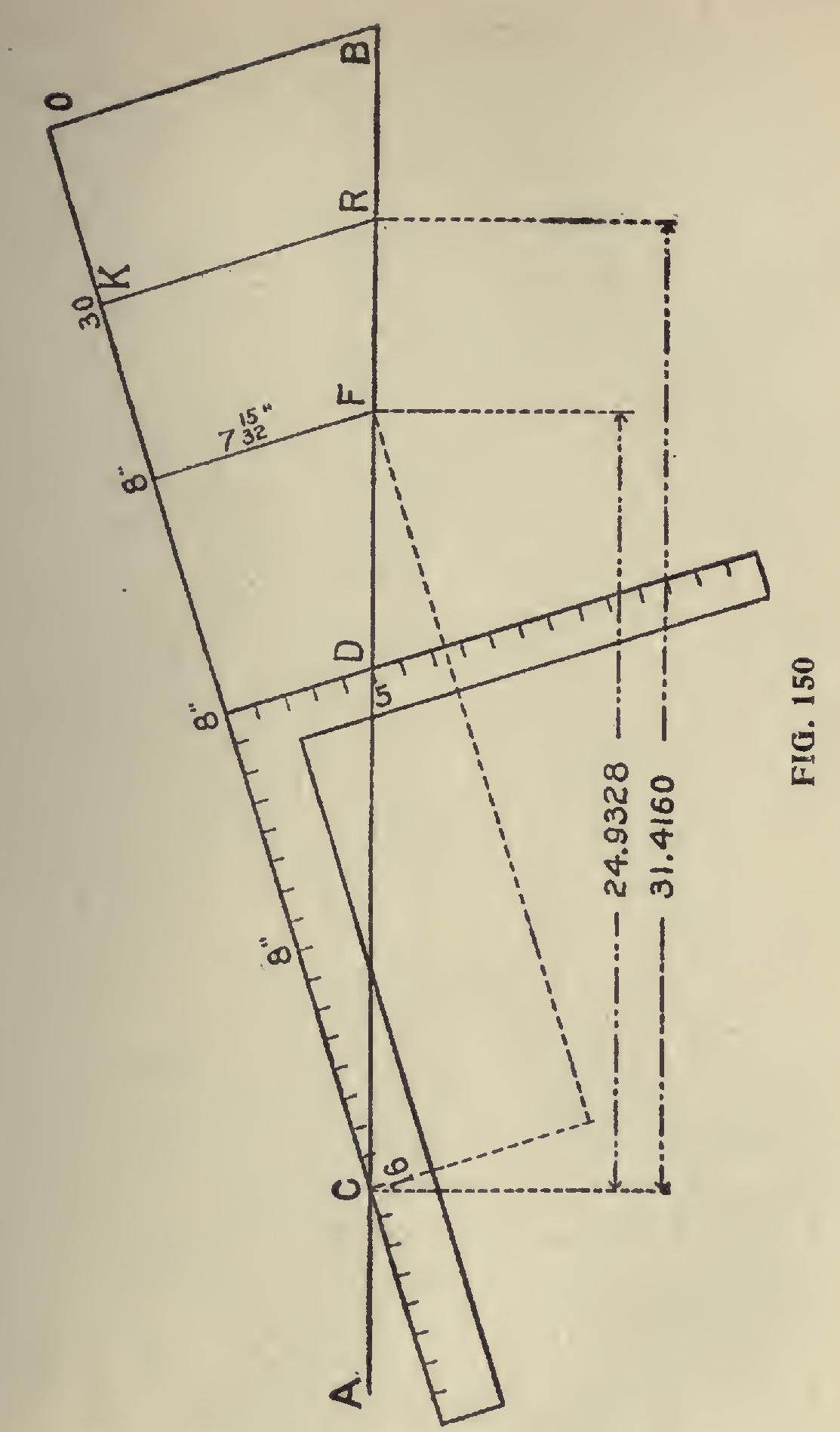
Now, to prove this, let us proceed as follows: Diameter = x 3.1416 = 31.4160, or nearly thirty-one inches and fifteen thirty-seconds of an inch. Now, if we measure C R, we will find that the distance is exactly 31 . 4160 inches, and is, therefore, the answer sought. It will be seen by these ex amples that the circumference of circles may be easily obtained when the diameters are known. So, also, may the diameters be found when the circumferences are known, for by laying off the circumference on the line A B, as C D in Fig. 150 for instance, and then applying the square as there exhibited, and dividing the distance from the heel of the square to the point C into three equal parts. One of these parts is the diameter of the circle whose circumference equals the distance from C to D.

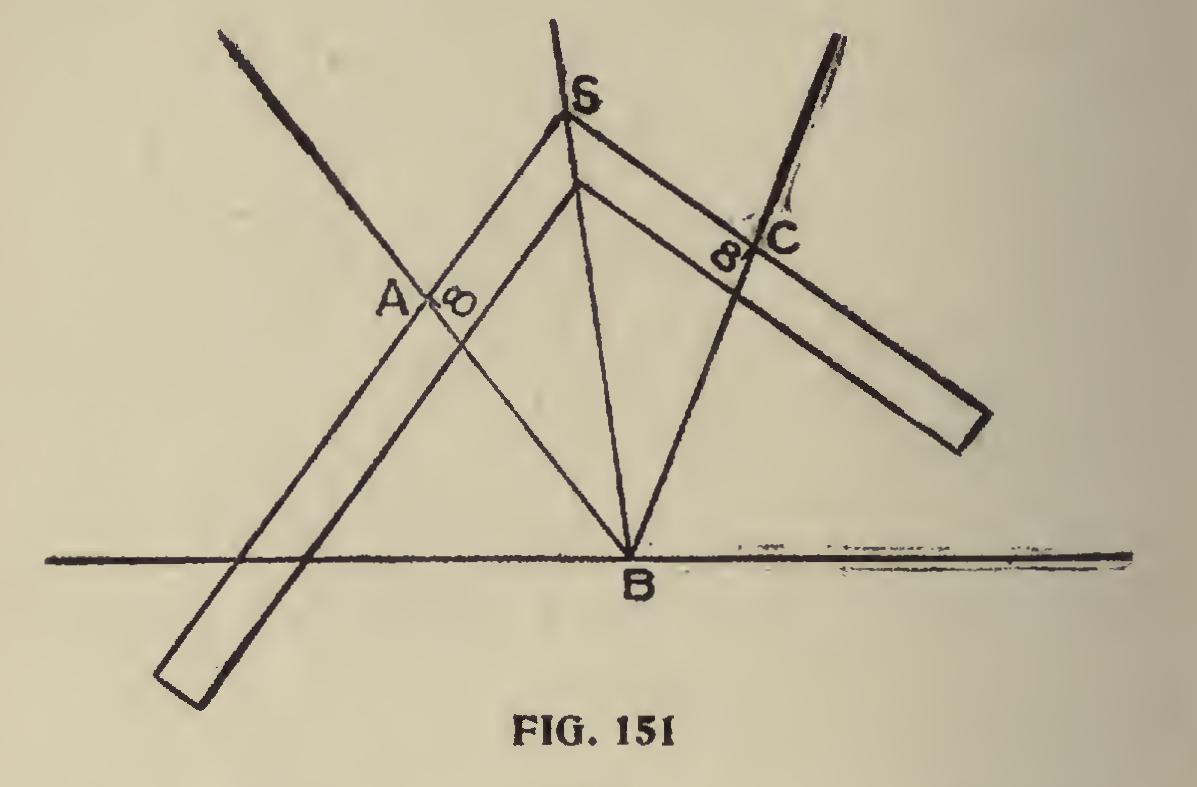
Method of Dividing Angles.—A B C, Fig. 151, is an acute angle. We wish to divide it. Measure up from B to A any distance, make B C the same distance, place the square on the points as shown on A and C, keeping the distance on the blade and tongue the same, then the heel or corner of the square, S, will give the points through which to draw a line passing through the angle at B, and the division will be complete.

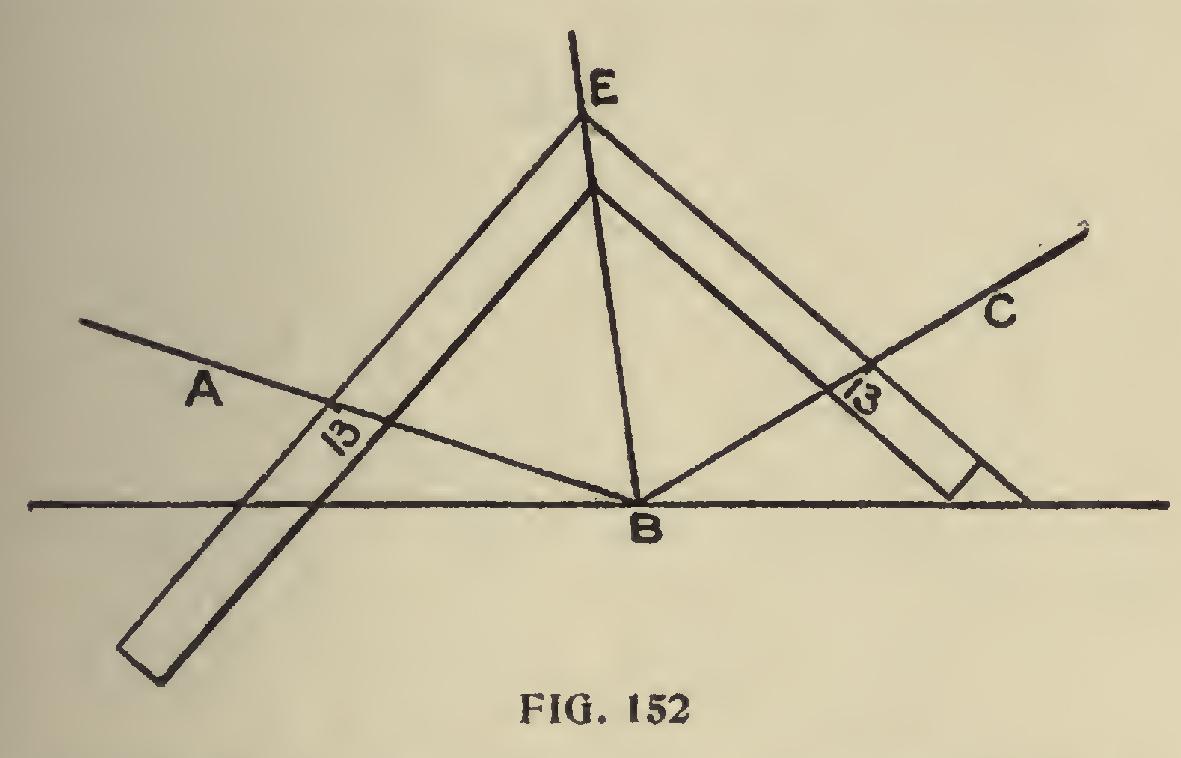
Again: Let Fig. 152 be an obtuse angle; make B A and B C equal. Apply square as shown, keeping equal distances on the blade and tongue at the points of contact A and C. The point E on the heel of the square will be one point from which to draw a line through B, which forms the division of the angle.

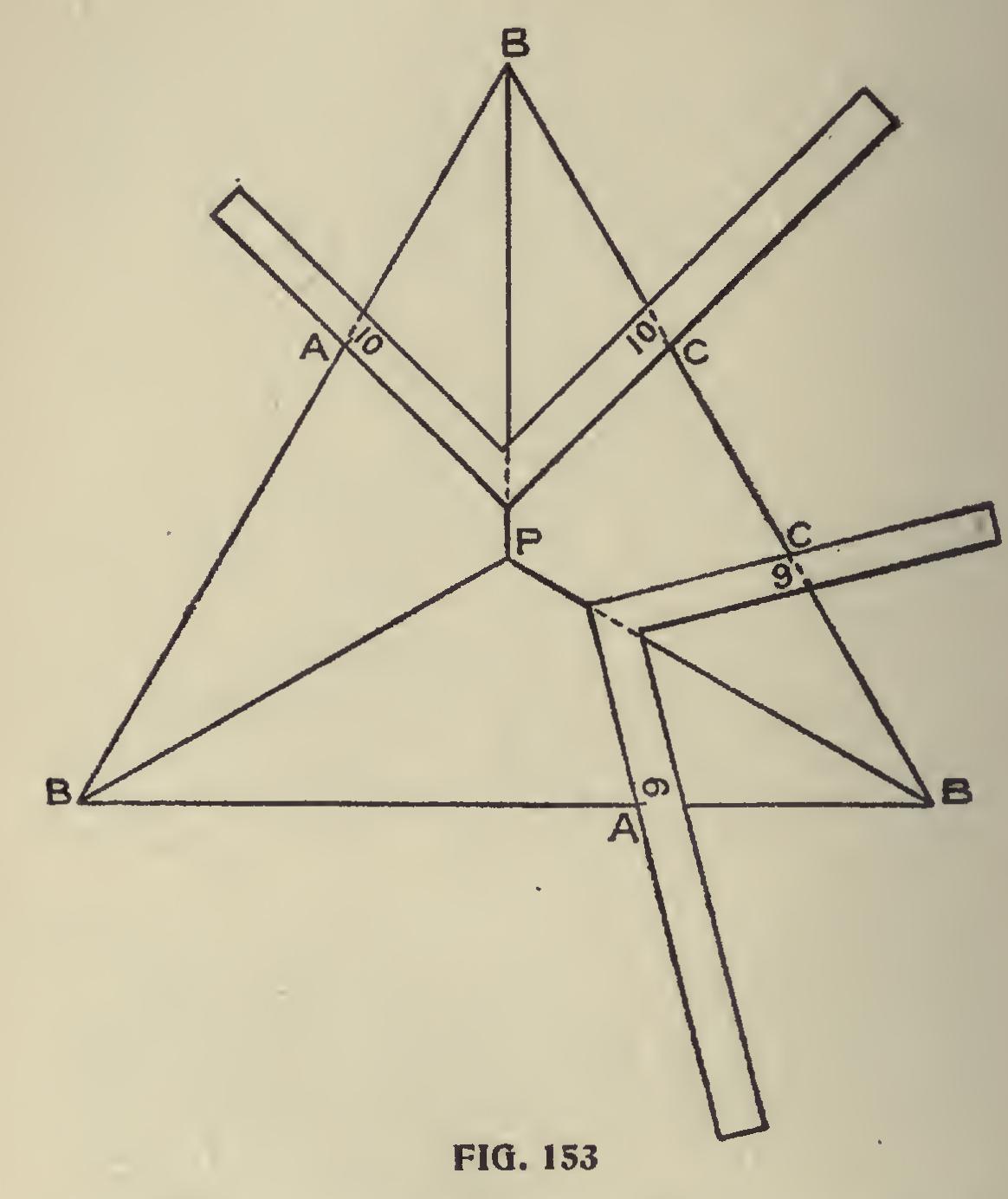
In Fig. 153 we show a number of angles, which are treated same as the foregoing. At the junc tion of the lines drawn from the angles B B B, the center of the triangle is found at P.

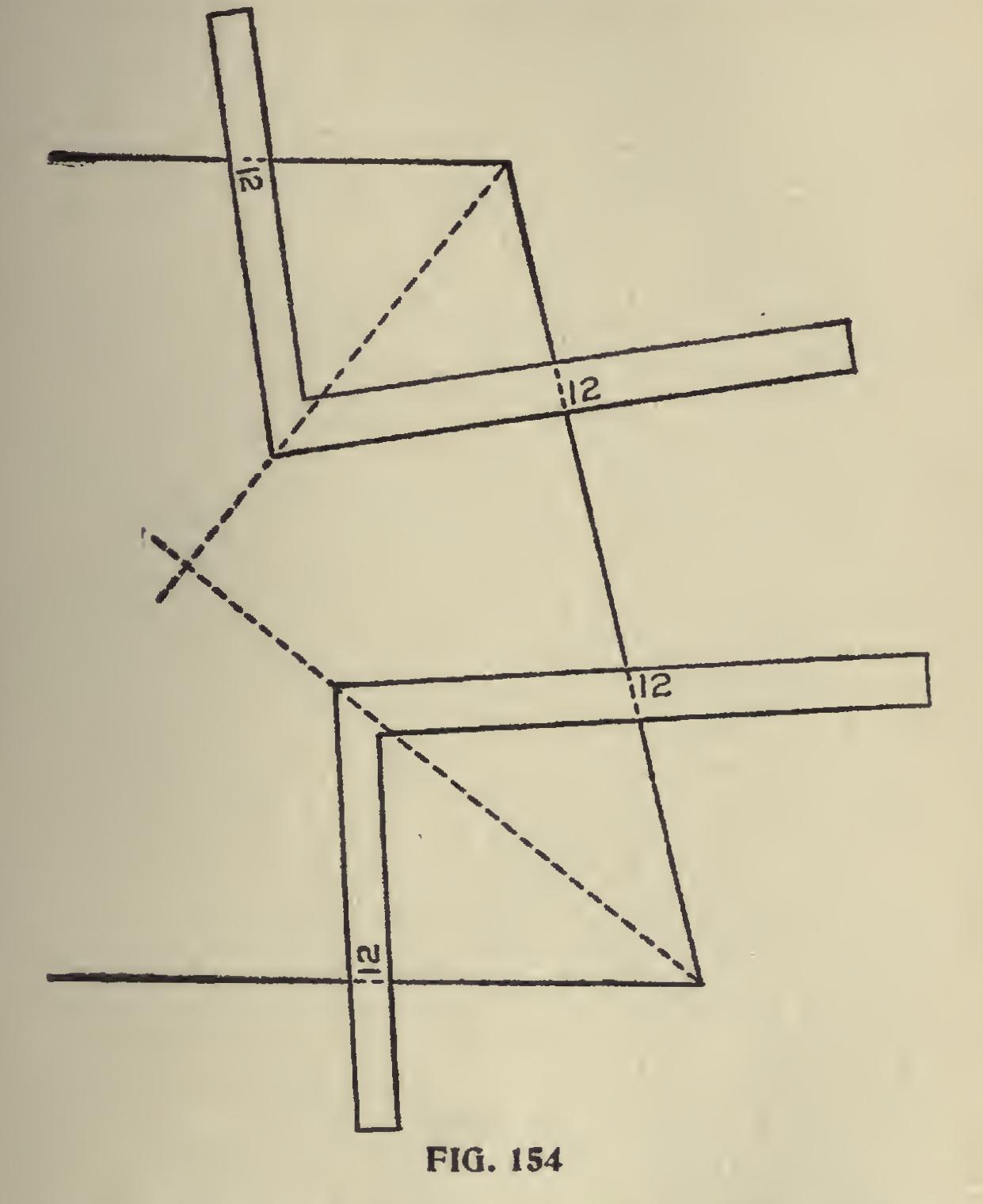
This method of bisecting an angle is very use ful, inasmuch as the cut or miter of any mouldings placed at any angle on a flat surface may be obtained. This is shown at Fig. 154, which may

be a panel or other like surface. This diagram shows that angles of any form and in any posi tion may be equally divided by a proper use of the steel square.

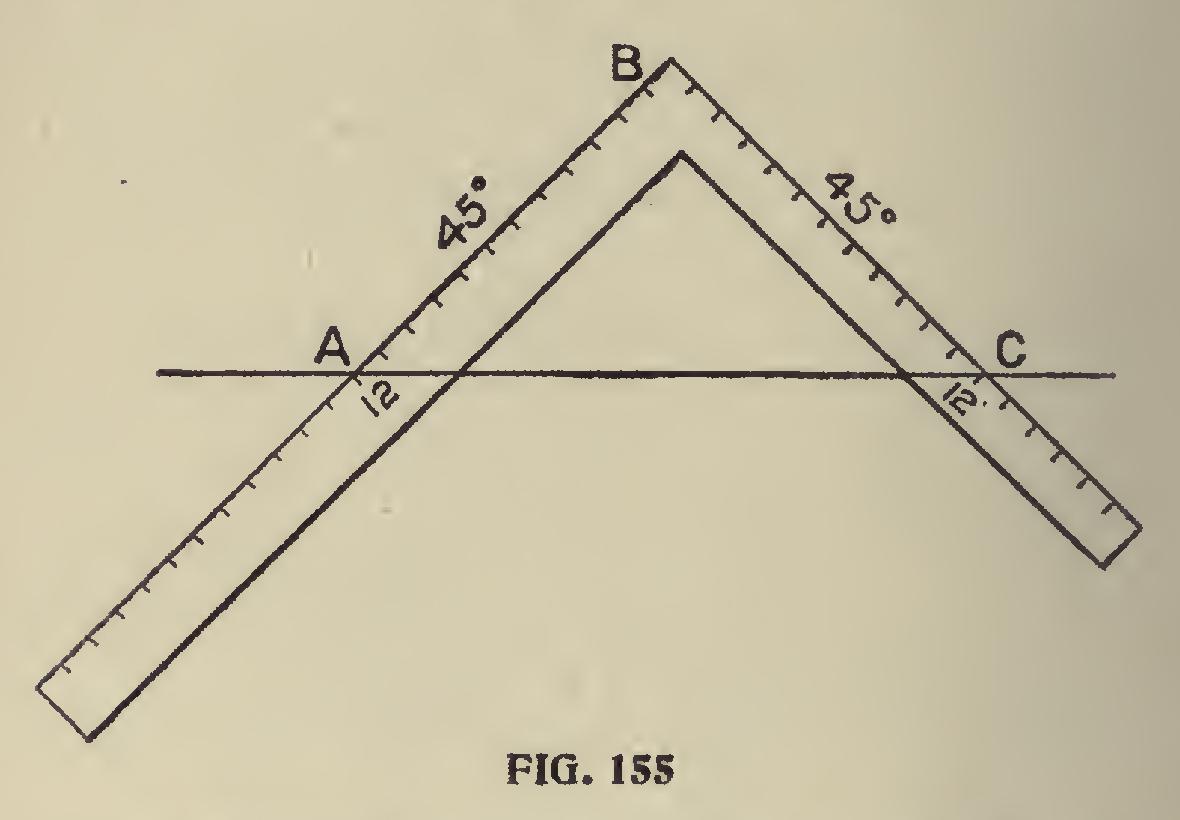
To Form a Template or Set Square.—Suppose we want to find the angle 45 degrees on a board, we mark any two points A C, Fig. 155, on the edge of a board; apply the square as shown, keeping its sides on A C ; then the distance on each side of the square being equal, measuring from its heel or corner B gives the angle 45 degrees. If this portion be cut out it will form a templet or set square, which is very useful in drawing. The lines A B and C B are true miters, or angles of 45 de grees, with the line A C as their base.

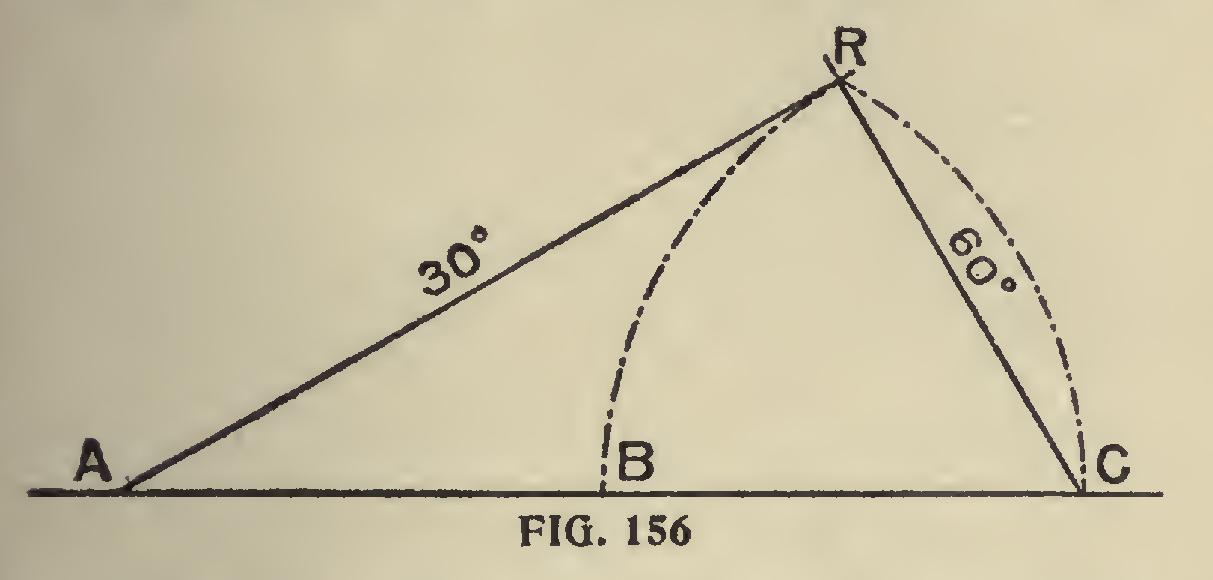
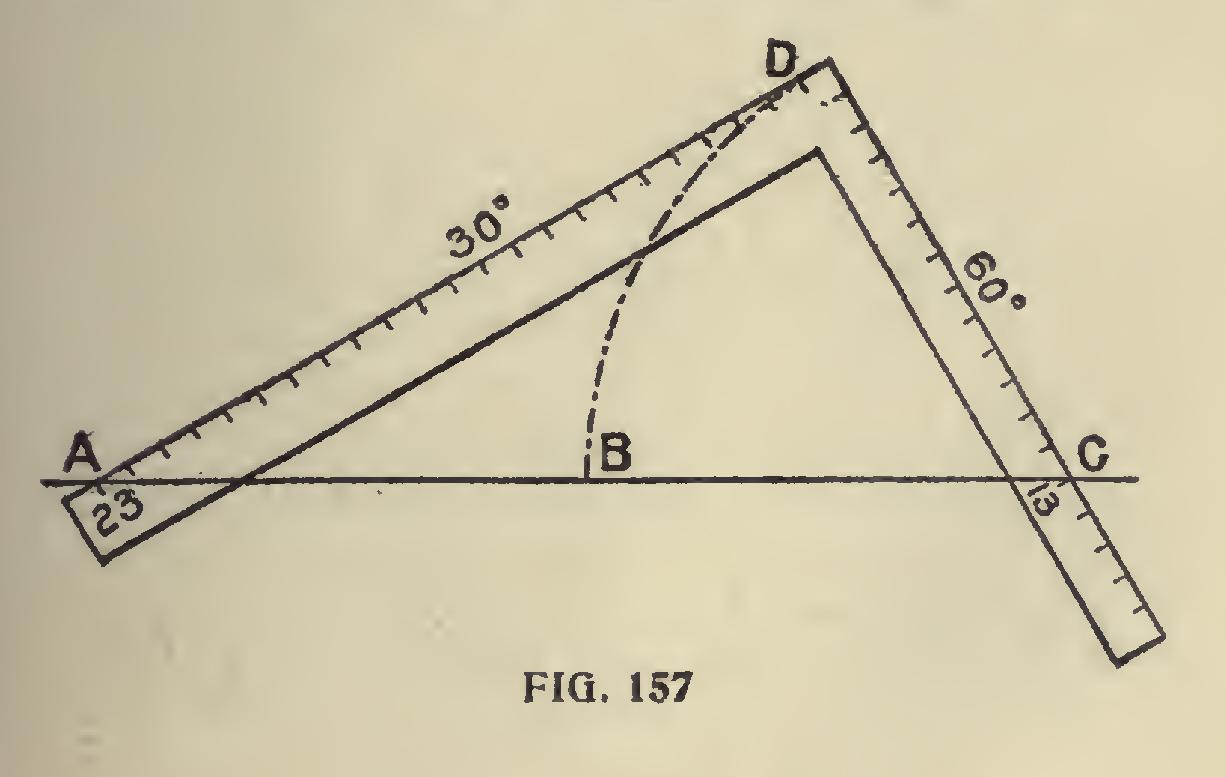
In Fig. 156, A, B, C, R show the lines for form ing a set-square having 60 degrees on the line C R, and 30 degrees on A R. This figure is formed with compasses, as follows : Make A C length of base line; let B be half the distance between A C. From C B as centers and radius make the in tersection at R, then by joining A R and C R the angles 30 degrees and 60 degrees are formed. This is the principle. To do all this with the square, simply take 23 inches on the blade and 13 inches on the tongue, and place these points on the line A B C, Fig. 157, and you have the angles at once. If the figure is greater than the square can cover, then continue the line A D to the length required; then square down until the line cuts A B C, and the work is done. If a smaller figure is wanted, measure off on A D, or A B C, and square over.

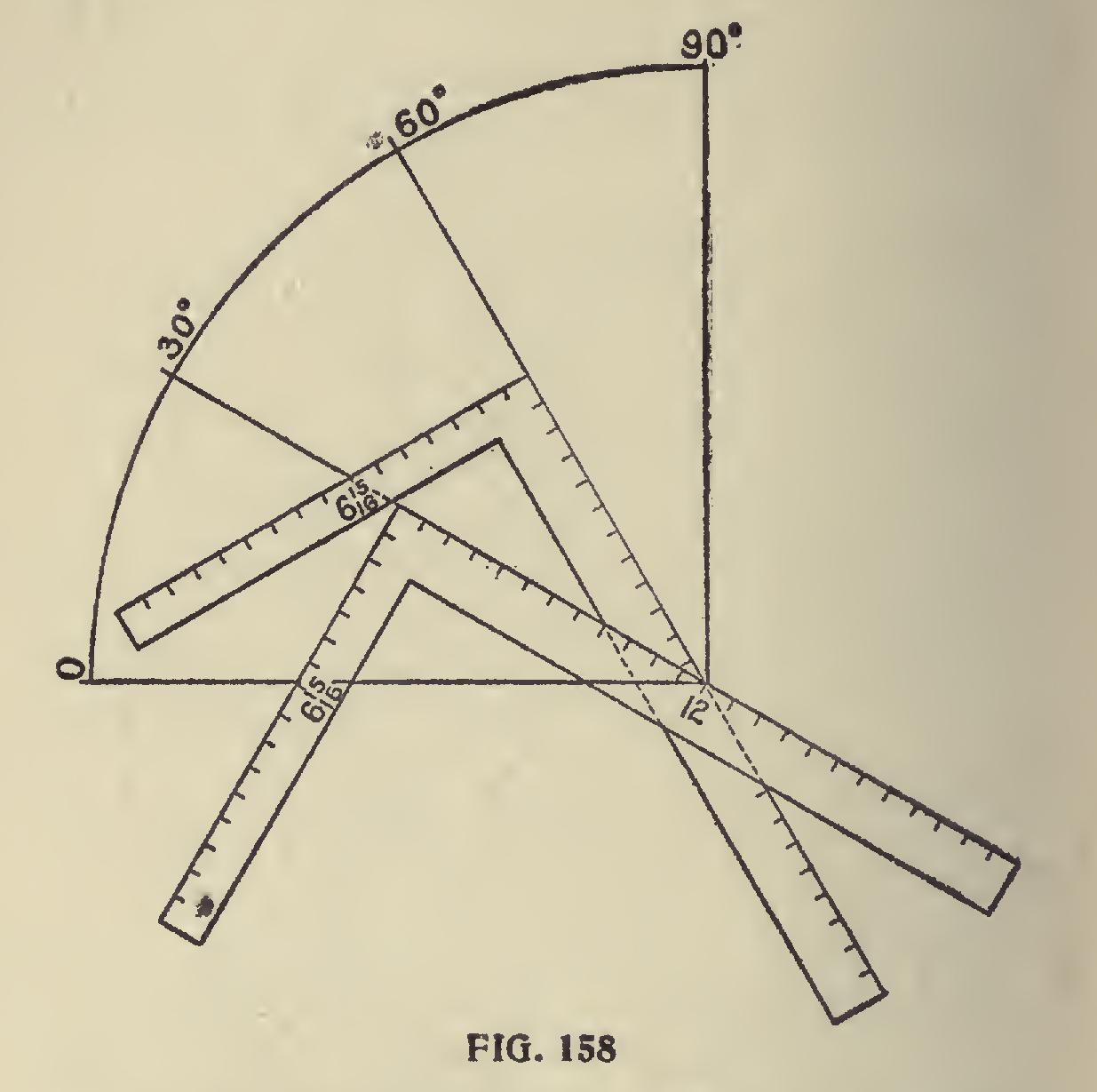
In Fig. 158 we show a quarter of a circle tri sected or formed into angles of 30, 60 and 90 de grees: 12 and 6 and 15-16 by the square will give 30 degrees and the remainder will be 60 de grees. These are things to remember, as the car penter and joiner will find them very useful in his everyday work.

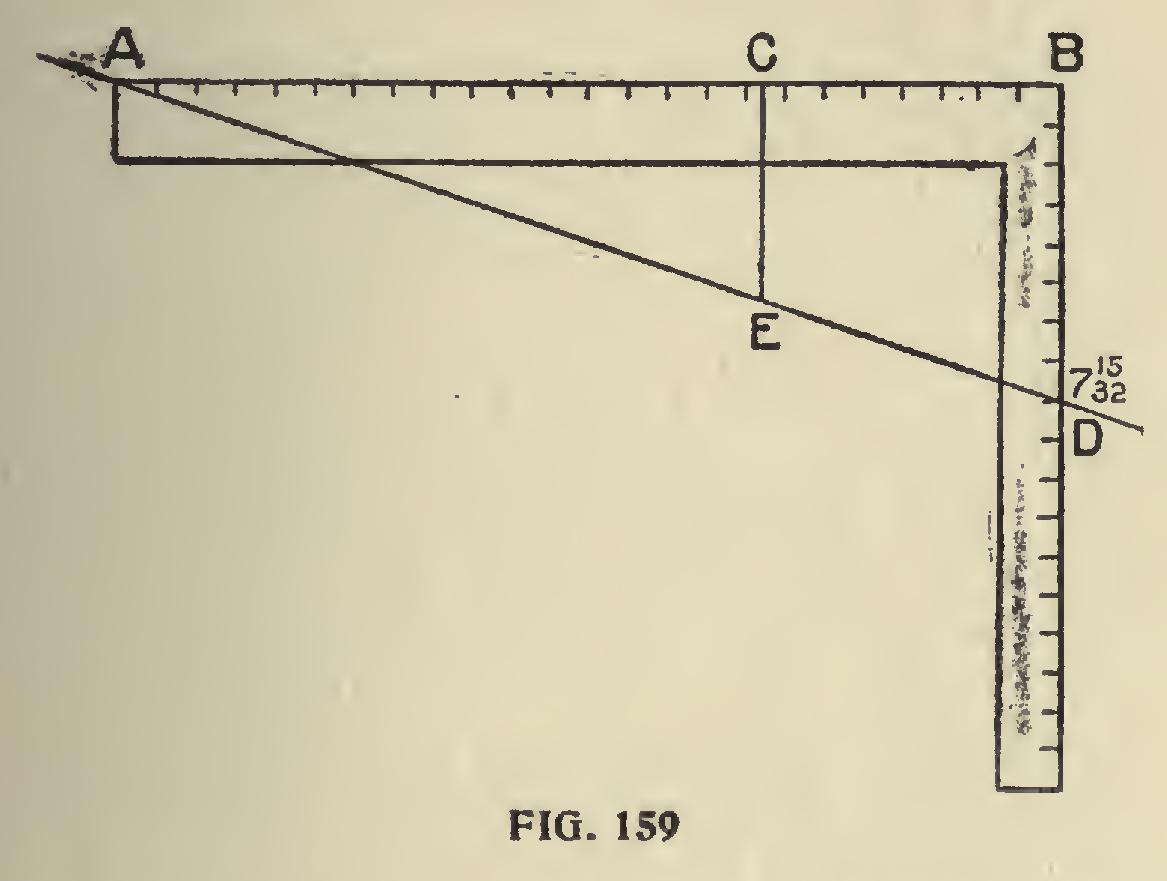
Other Methods of Obtaining Circumference of Circles of Given Diameters.—Fig. 159 shows how the circumference of a circle may be obtained by the square, the diameter being given. The solution of this problem by use of the steel square has been attempted by a number of writers on carpentry. It is not claimed that absolute' cor rectness is obtained in the following way, but it is claimed for this method that it is the nearest ap proach to correctness yet made by using the steel square. The method is not new, it having been employed for a number of years. Let A D rep resent the straight edge of a board, say 10 inches, or 12 inches wide; place the end of the blade of square at A, and let D on tongue be 7 and 15-32 inches. Take three diameters from A to C, and square down a line from C, cutting A D at E; then A E equals the circumference. A circle whose diameter is eight inches would have a circum ference equal to the line from A to D by this rule. It will be seen by this that any right angle whose base is 24, and having an altitude of 7 and 15-32, forms a constant by which any circumfer ence may be obtained by spacing three times the diameter on the line A B, and squaring down as at C, the hypothenuse being the required answer. The line A B may be continued indefinitely, being careful to retain the proper angle as shown in diagram.