Miscellaneous Rules

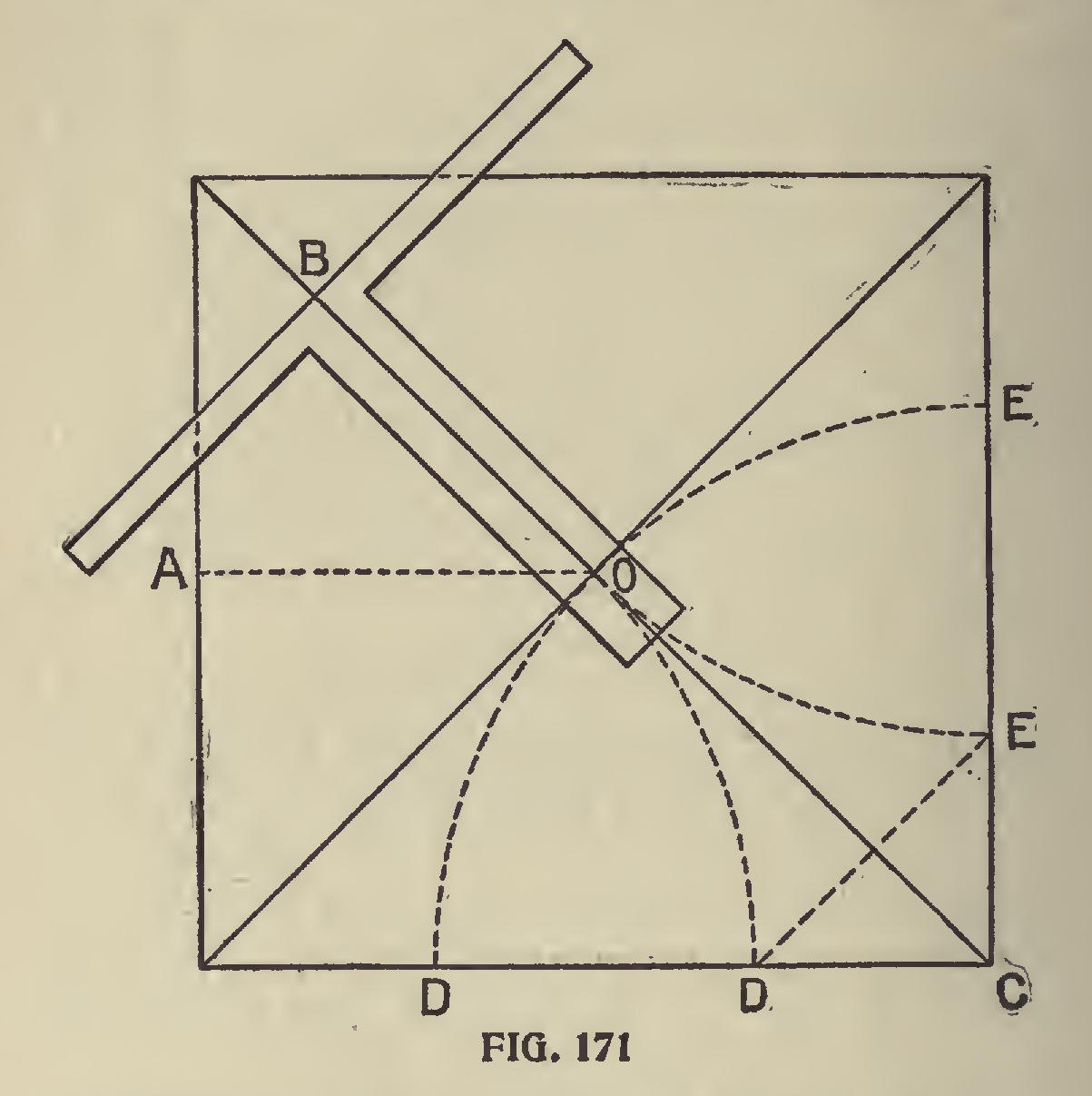
To Produce an Octagon.—Fig. 171 shows how an octagon can be produced by the aid of a steel square. Prick off the distance A 0 equal to half the distance of the square; mark this distance on the blade of the square from B to 0, place the square on the diagonal, as shown, and square over each way. Do the same at every angle, and the octagon is complete.

To obtain the same figure with the compasses, proceed as follows: Take half the diagonals on the compasses, make a little over a quarter sweep from C, and at the intersection at D and E, then D-D or E-E form one side of an octagonal figure.

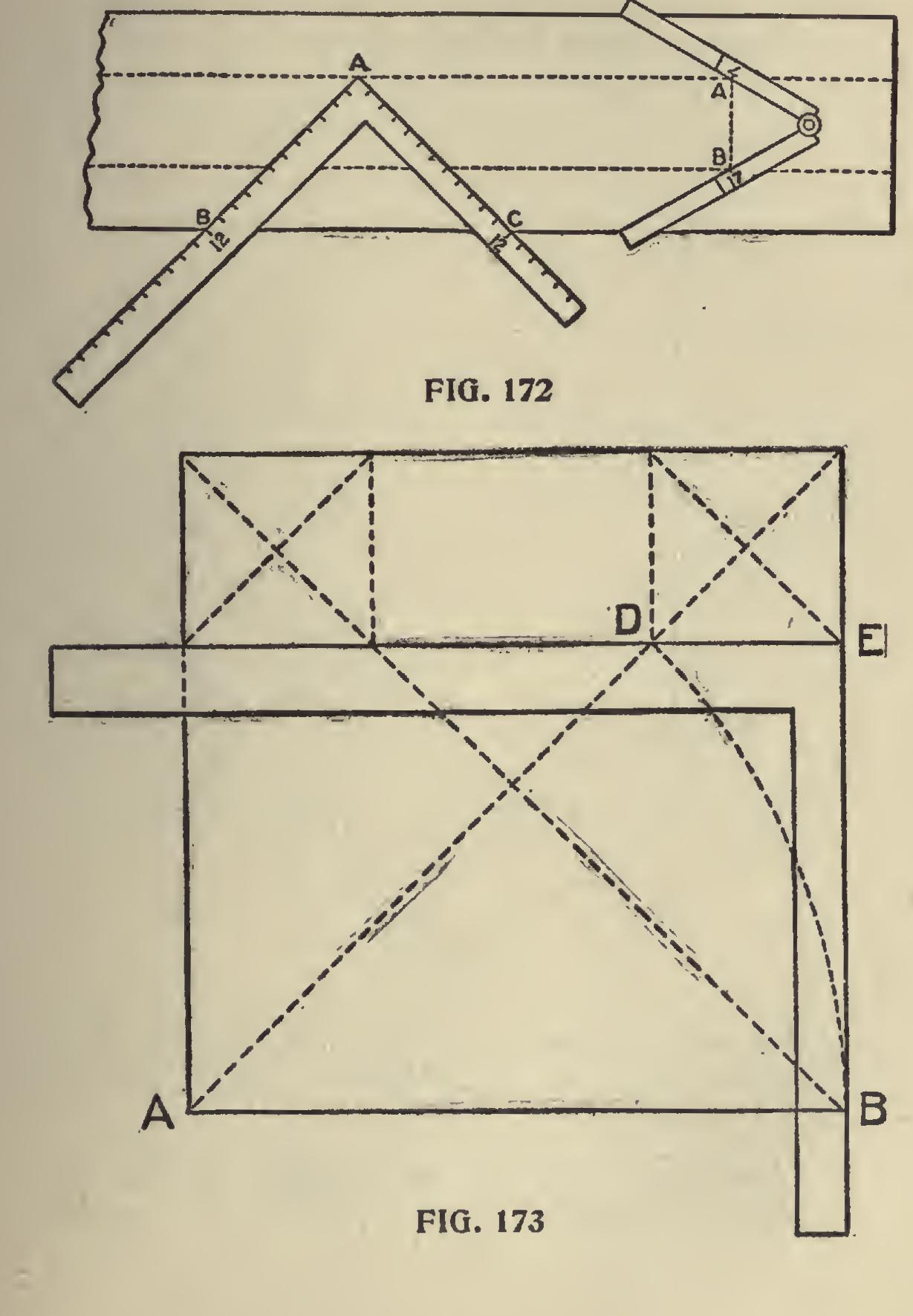
Again: Take a piece of timber twelve inches square, as in Fig. 172; take twelve inches on the blade and tongue from A to B, and A to C, mark at the point A, operate similarly on the opposite edge, and the marked points will be guides for gauge-lines for the angles forming an octagon. The remaining three sides of the timber can be treated in the same manner.

These points can be found with the carpenter's rule as follows: Lay the rule on the timber, partly opened, as shown in the cut, prick off at the fig ures 7 and 17 as at A and B, and these points will be the guides for the gauge lines. The same points can be found by laying the square diagonally across the timber and pricking off 7 and 17.

To Make a Moulder's Flask Octagonal, proceed as follows : The flask to be four feet across. Multiply 4x5 (as an octagon is always nearly as 5 to 12), which gives 20; divide by 12, which gives 1 and two-thirds feet, cut miter to suit this meas urement, nail into corners of square box, and you have an octagon flask at once.

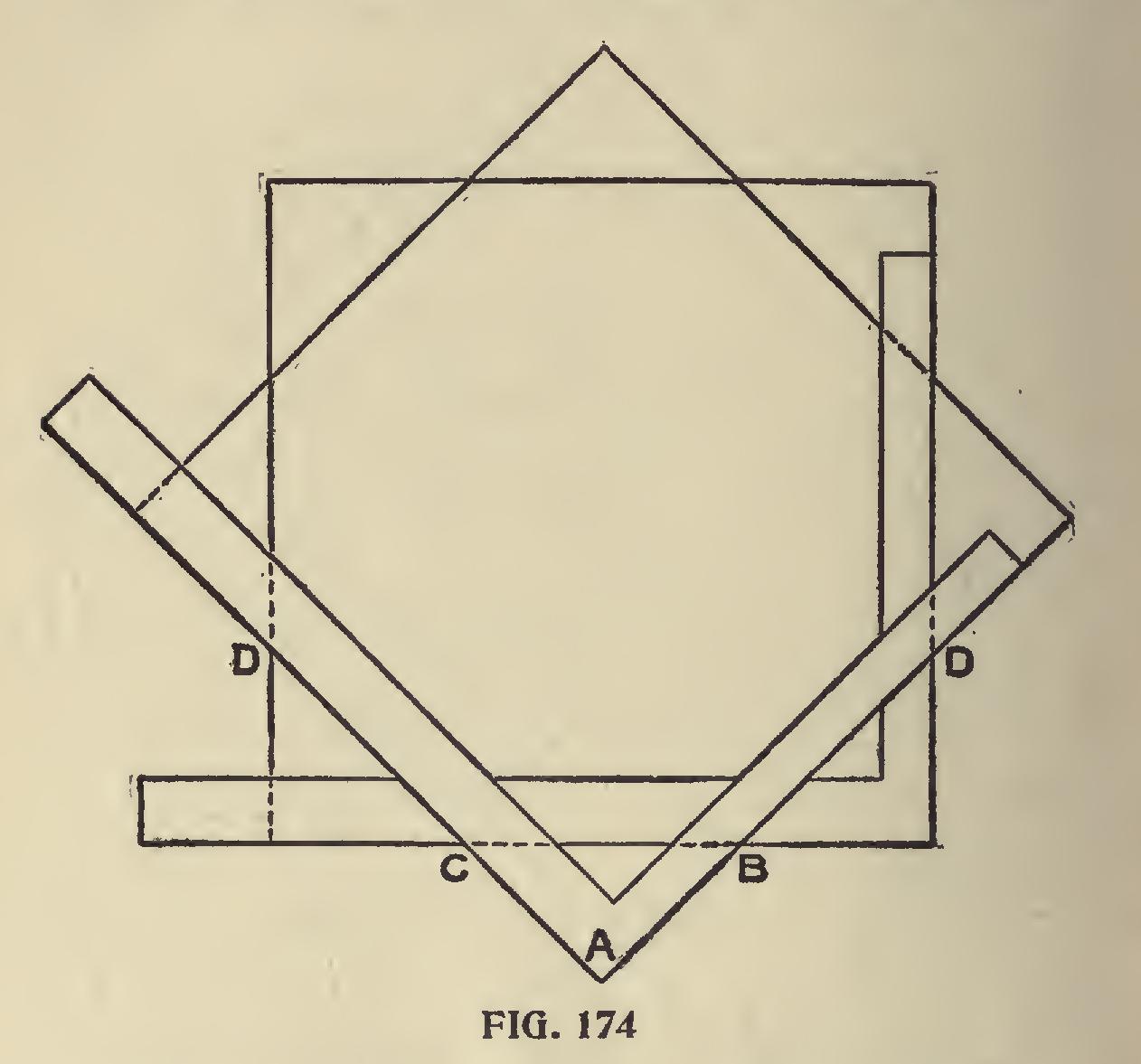
Another method of constructing an octagon is shown in Fig. 173.

Take the side as a b for a radius, describe an arc cutting the diagonal at d; square over from d to e, and the point e will then be the gauge-guide for all the sides.

Another method (Fig. 174), is to draw a straight line, c b, any length of desired side ; then let a b and a c be corresponding lengths on the blade and tongue of the square, mark along either and move the square and mark also. Now use the square the same as before, and the marks d c and b d will equal c b.

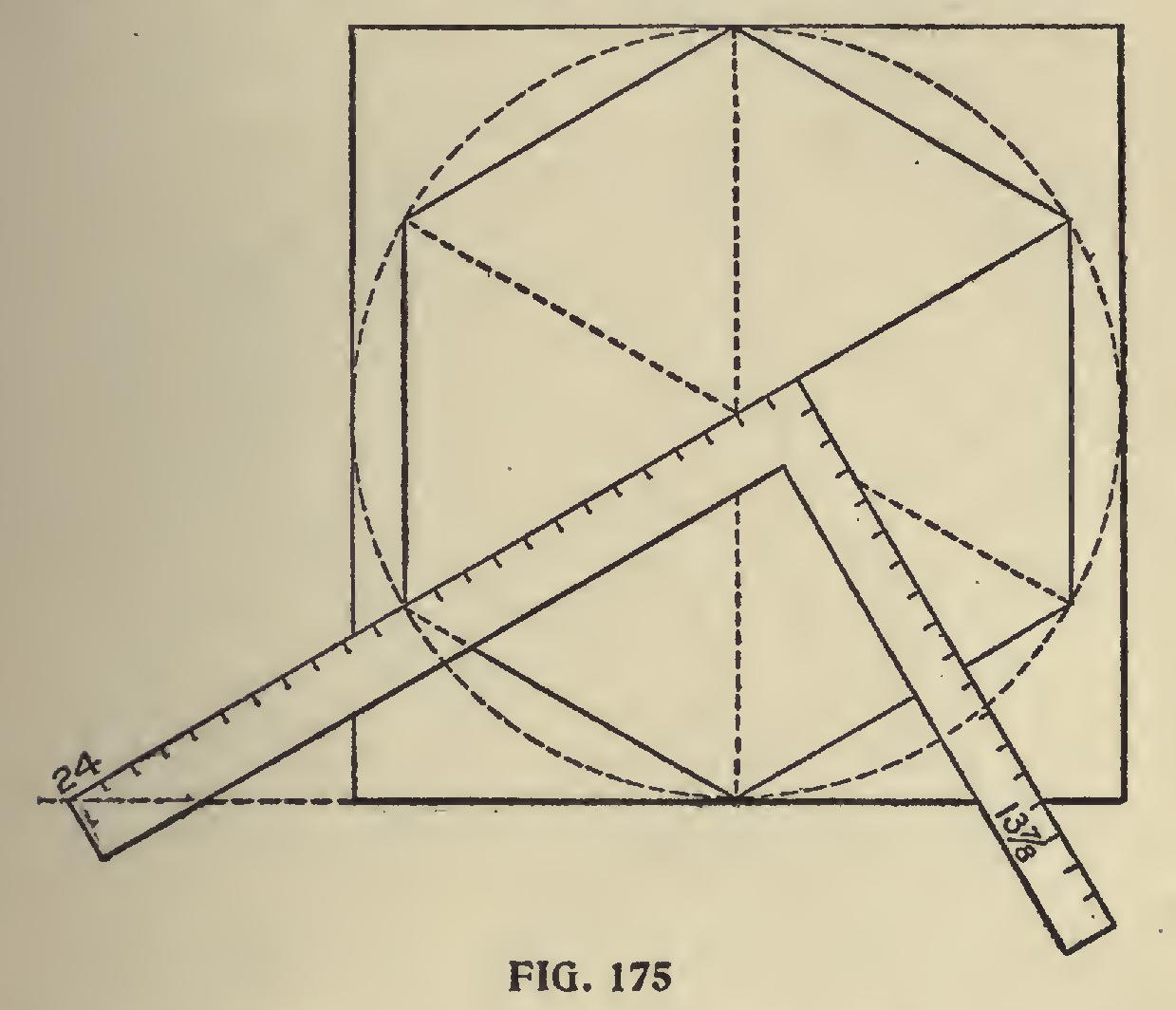
To Make a Hexagon, Fig.

175, take 13 and inches on the tongue and 24 inches on the blade, and apply as shown on a base line which forms a square around the figure.

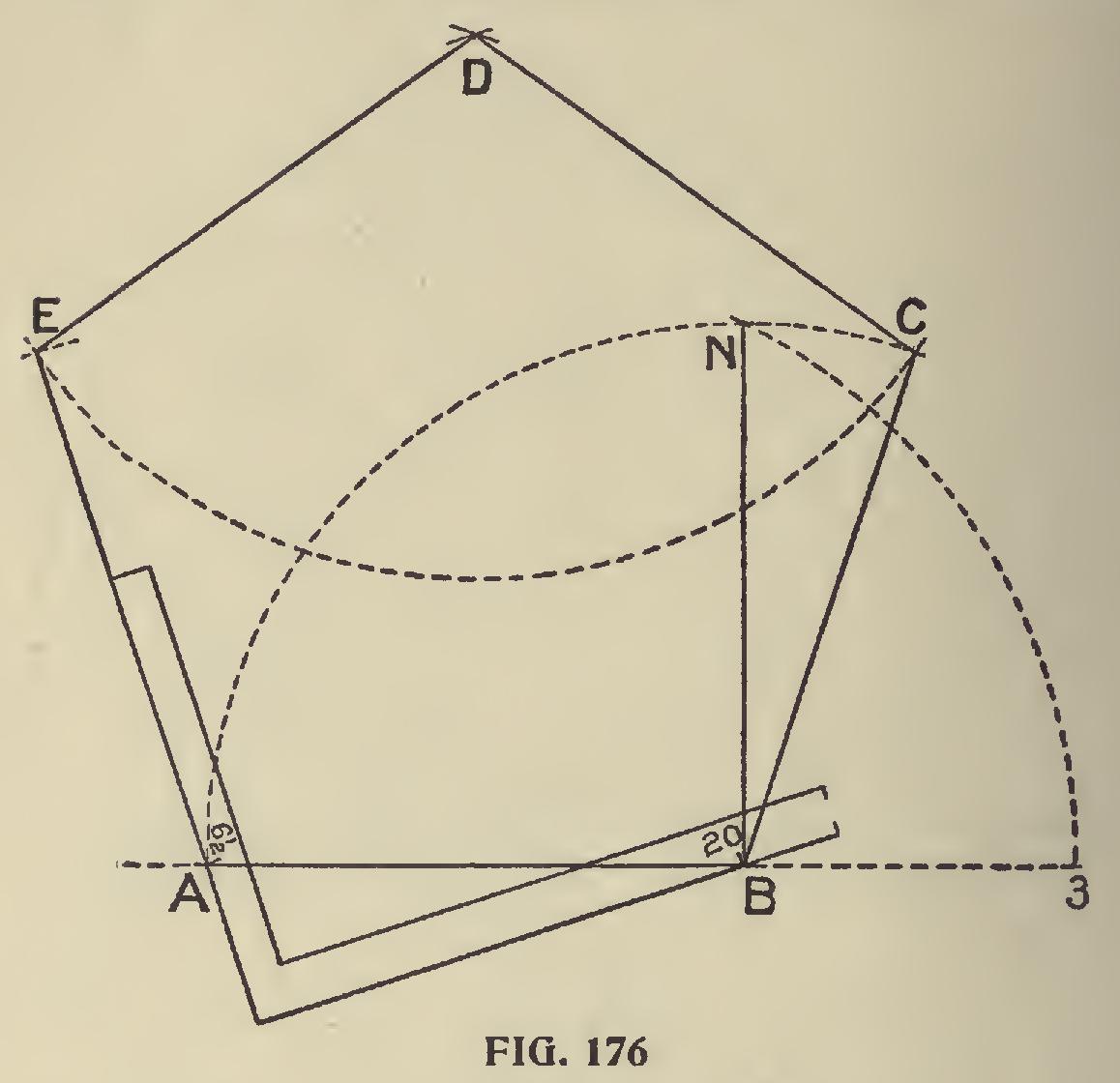
Construction of a Pentagon or Five=sided Fig ure.—There are several methods of forming this figure, but we prefer the following: On a given line let A B, Fig. 176, be the length of one side; divide this into two equal parts, marking it as at 2. From B square up a line, and make B N equal to A B, then with 2 as a center and 2N as radius, describe the arc, cutting the line A B at 3. Now take A3 for radius, and from A and B as centers make the intersections at D; then from D, with a radius equal to A B, describe an arc as shown; then using A and B for centers, intersect the arc in E and C; connect these pionts together with straight lines, and the pentagon is complete.

This is a scientific way of forming this figure, but it may be obtained much easier by the square.

It may be necessary to explain that in regular equal-sided polygons the angles are equal, so any side of a regular polygon may be used for a base line. Let this fact be remembered, as it is im portant the student should keep it in mind when dealing with any problem connected with polygons, where the steel square is used : By careful examina tion of Fig. 176 it will be seen that the outer edge of the tongue of the square is in line with one side, A E, of the pentagon, measuring down below the base line, A B, six and one-half inches; then the 20 inch mark on the outer edge of the square will also touch the base line, A B, This position of the square then gives the exact inclination of the side of the pentagon with the base. Now if we reverse the square and place the 61. inch mark at B, and the 20 inch mark on the line A B, we give three sides of the figure. Now make the distance from A to E the same as A B, and we have the length of that side. Perform the same operation with B C. Then using A E and B C as base lines, we can form the complete figure. This shows how any pentagon having equal sides can be formed with the square.

We wish to recall again that 6i inches on the tongue and 20 inches on the blade give the proper angle for forming pentagons.