Miscellaneous Rules

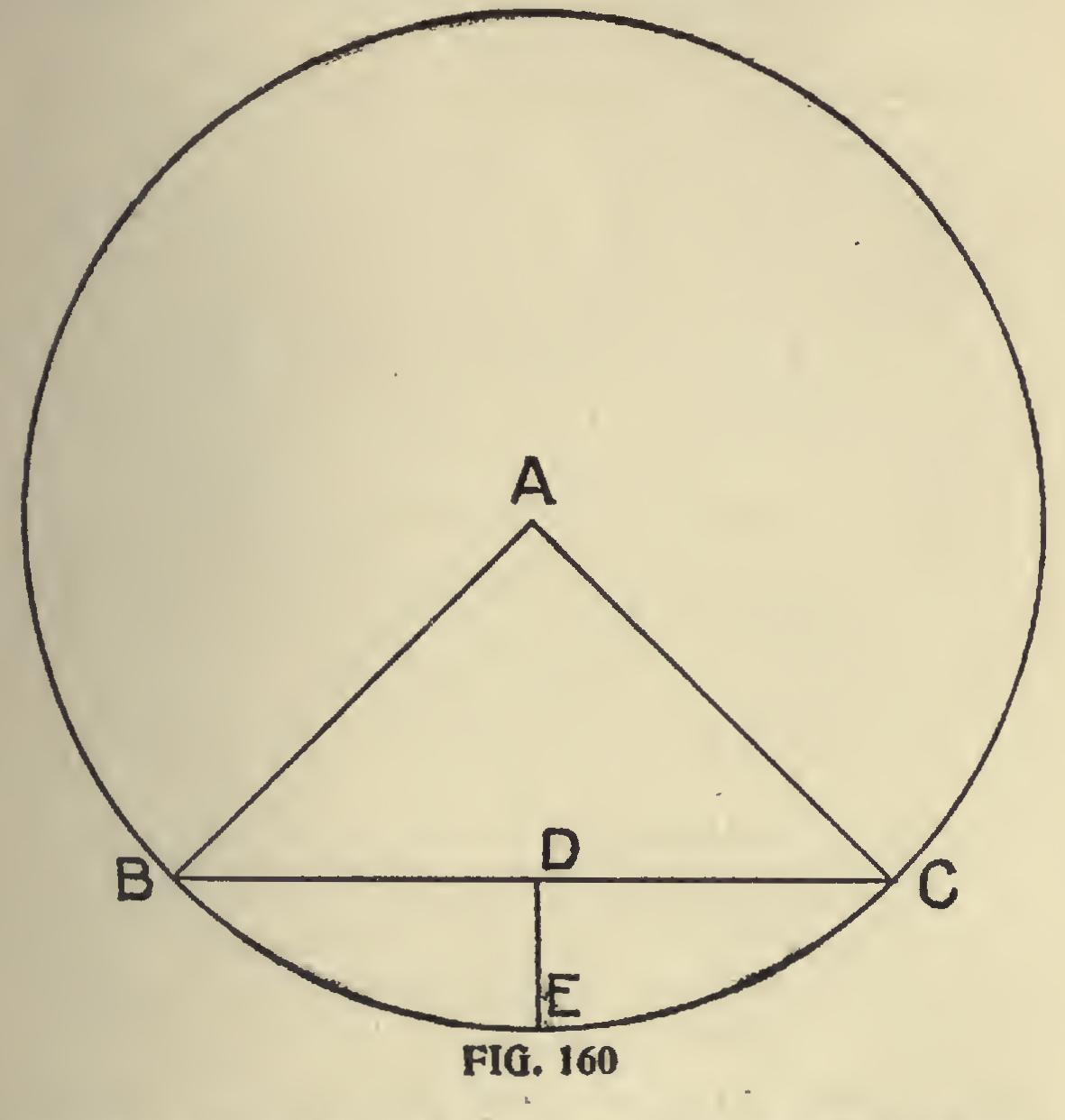
Fig. 160 shows a method by which the circum ference of a circle may be obtained from the diam eter. This will be found very convenient in almost all the trades; particularly is it so for sheet-metal workers, carpenters, plasterers and coopers.

Describe a circle in some proportion to the actual work, say one inch to the foot; then apply the heel of the square at the center of the circle, as at A, then project the lines A B and A C as shown. Now connect the points where the radial lines touch the circle by the line B C, and from the middle point of this line draw the line D E to the circumference. To obtain the circum ference of the circle, add to three times the diam eter the distance D E, which will give the desired result practically correct.

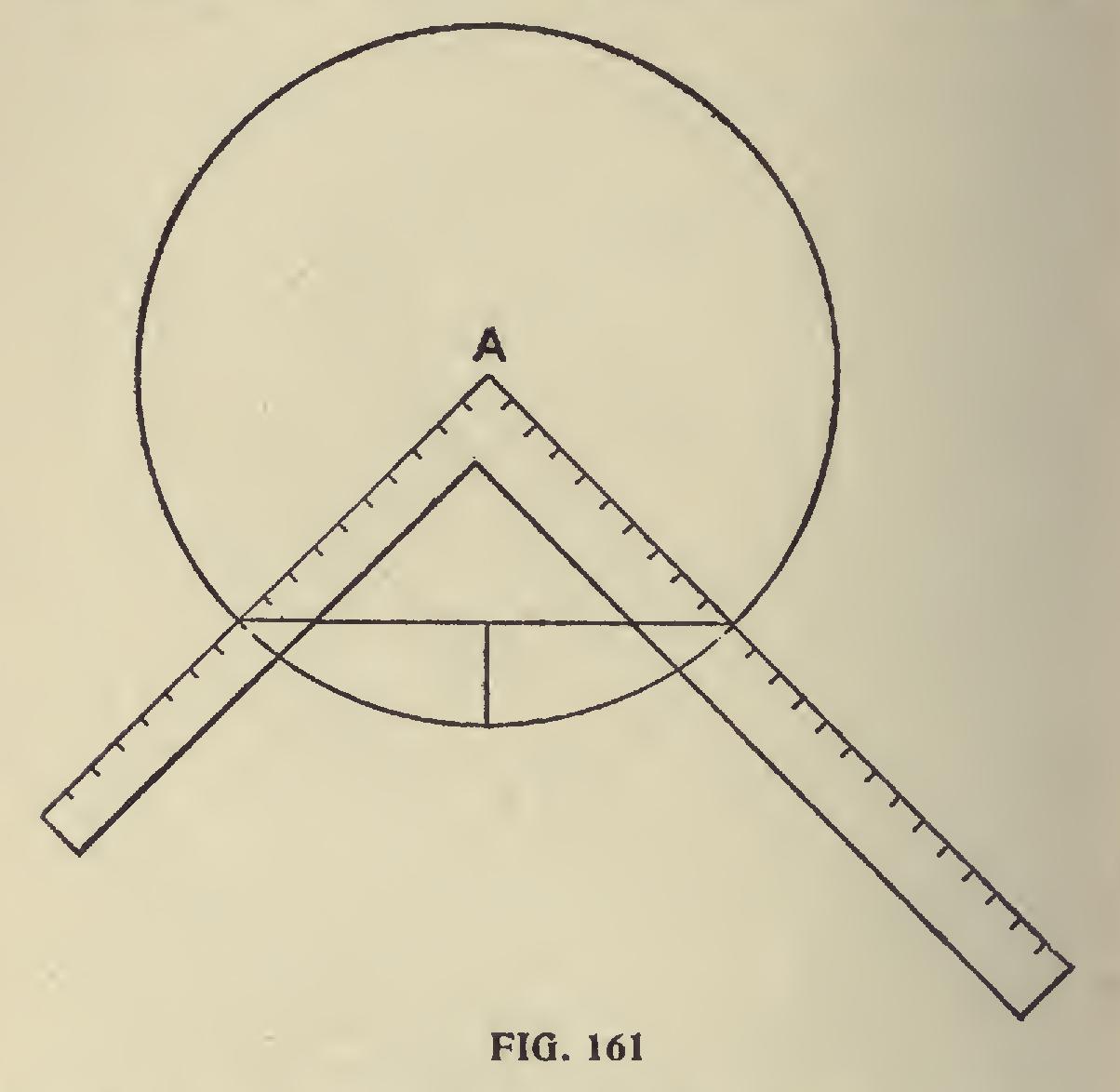
In Fig. 161 we give a practical illustration. Suppose we have a circular tank, or a sheet-metal vessel of any sort that requires to be twenty feet in diameter. Draw a circle twenty inches in diameter. This is one inch to the foot; place the square with the heel on the center as at A, draw lines along side blade and tongue as shown, cut ting circumference, then at the junction of these lines draw a line same as B C in Fig. 160, then draw the short line from the center of the line B C, Fig.

160 and you have the circumference near enough for all practical purposes. It will be seen at once how useful this method may prove to the mechanic and how easily applied. For getting the length of hoops, or the number and breadth of staves for a circular tub, it will prove quite a useful method.

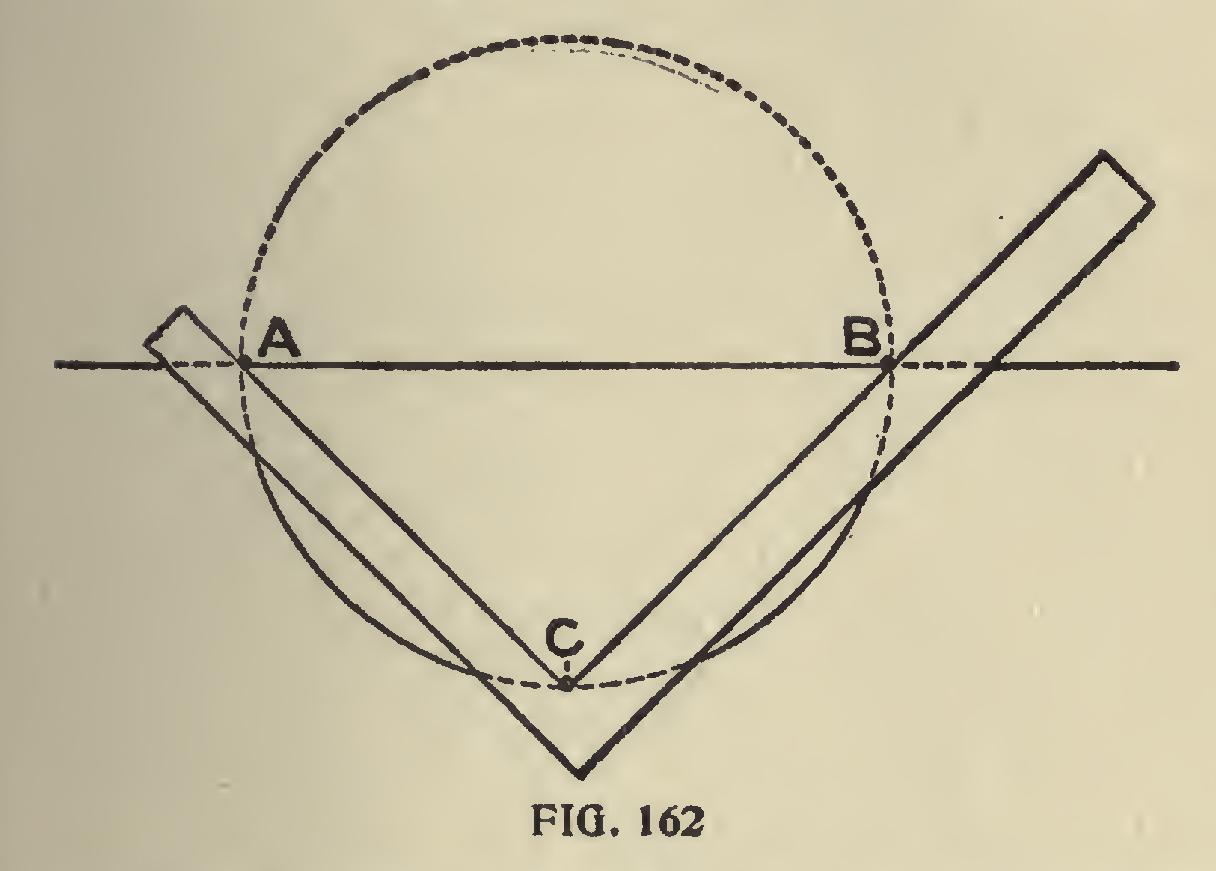
To Describe a Circle with the Aid of the Steel Square.—This may be accurately done provided the diameter of the circle does not exceed the length of the shorter member of the square.

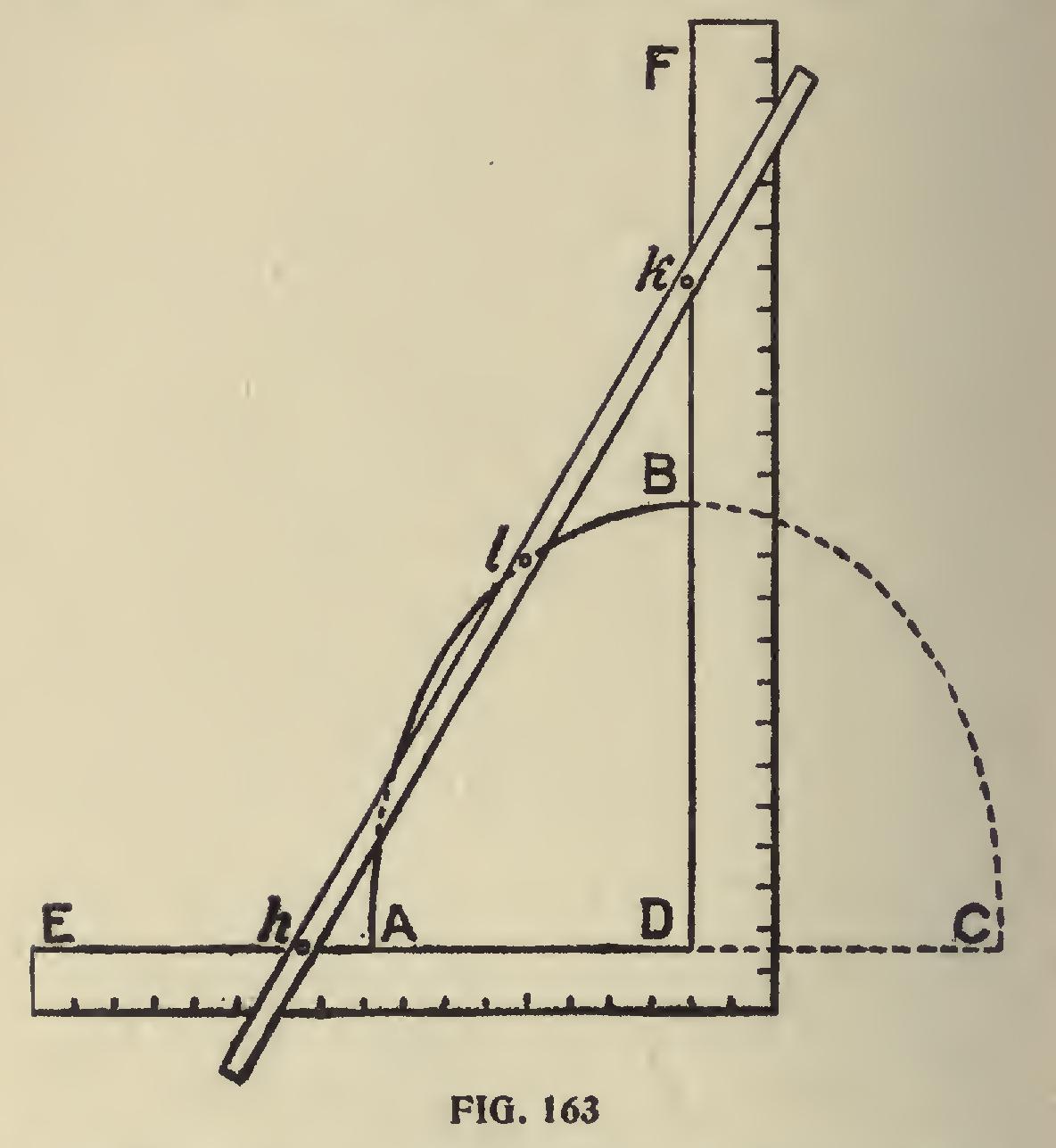
In Fig. 162 let A B be the desired diameter and at these points drive small brads. Then place the inner edges of the square as shown touching the brads and with a pencil at the angle of the square as at C move the square, keeping it close up to the brads, and it will have made a true semi-circle. Reverse the square and repeat the operation and the true circle will be complete How Square May be used to Form Ellipses.— In Fig. 163 we show how the square can be used, in lieu of the trammel, for the production of el lipses. Here the square, E D F, is used to form the elliptical quadrant, A B, instead of the cross of the trammel; h 1 k may be simply pins, which can be pressed against the sides of the square while the tracer is moved. In this case the ad justment is obtained by making the distance, 111, equal to the semi-axis minor, and the distance 1 k, equal to the semi-axis major.

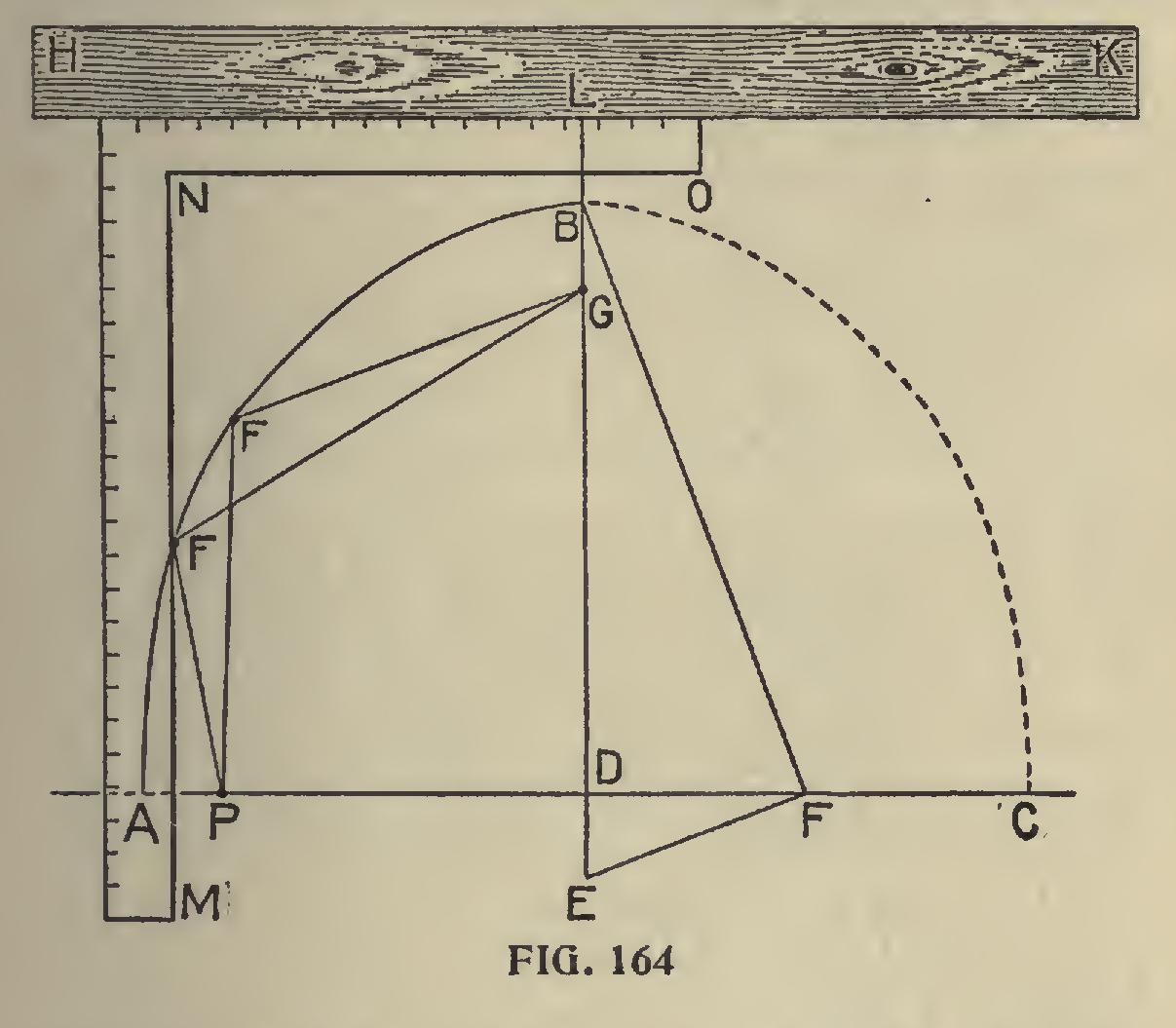
To Describe a Parabola.—Fig. 164 shows a method of describing a parabola by means of a straight rule and a square, its double ordinate and abscissa being given. Let A C be the double ordi nate, B the abscissa. Bisect DC in F; join BF, and draw F E at right angles to B F, cutting the axis B D produced in E. From B set off B G equal to D E, and G will be the focus of the parabola. Make B L equal to B G, and lay the rule on straight edge II K on L, parallel to A C. Make A P equal B G. Take a string P F G, equal in length to L E; attach one of its ends to a pin, or other fastening, at G, and its other end at P. If now the square be slid along the straight-edge, and the string be pressed against its edge M N, a pencil placed in the bight at F will describe the curve.

To Determine What Weight is Required to Balance Lever.—The two arms of a horizontal lever are respectively 9 inches and 13 inches in length from the suspending point; and a weight of 10 lbs. is suspended from the shorter arm, and it is required to know what weight will be re quired to suspend on the long arm to make it balance. Set a bevel on the blade of the square at 13 inches and the other end of the bevel on the 9 inch mark on tongue of square, then slide the bevel from 13 inches to 10 on the blade of square, and the answer will be found on the tongue of the square. It is easy to see how this rule can be reversed so that a weight required for the shorter arm can be found.

To Make a Semicircular Groove.—Sometimes the workman may have a semicircular groove to make, either as a pattern for casting or as a mould ing of some sort. Now it is a well known geo metrical fact that the angle within a semicircular circumference is a right angle; this being admitted, it may be taken advantage of in making such hollow forms as we have mentioned, and which we illustrate by the Fig. 165. The curve or semicircle may be worked out by a plane or other instrument, and to prove the correctness of the work, the steel square may be applied as shown. If the square touches at only two points, then the groove is not deep enough, or else it is too deep, in which case the operator must remove more stuff from the groove, or from the flat surface of the work, if permissible. By giving the square an oscillating motion, so as to make the corner sweep the entire surface of the curve, the accuracy of the work may be ascertained whenever the square is applied.