Pitches and Roof Framing

For the corresponding hip or valley for the pitch lines above the full pitch, use 81 on the tongue for the scale and 41 for the scale. It will be seen that by the reduction in the scale, taken on the tongue of the square, permits of many pitch lines on the blade, thereby increasing the rise to any desired height.

In this illustration we give the degree and minutes of pitch for the common rafter up to the full pitch. To find the same for the reversed pitch lines, it is only necessary to subtract the degrees here given from 90 degrees. Thus—to find the degrees for the full pitch when reversed, subtract 63° 26" from 90°. To do this it must be remembered that it is necessary to borrow one degree from ninety and that one degree is equal to 60" and should be expressed thus, 89° 60" 63° 26"=26° 34", which will be seen is the same as that for a 6-inch rise or the one-quarter pitch. (Also see Fig. 196.) By referring to the degree scale in Fig. 197, the degree of the other pitch lines can be very nearly arrived at by scale as shown by the quadrant.

We trust we have made it clear that by using the tongue of the square to represent the run, instead of the blade as is the custom of most other writers, permits of the pitch lines up to the full pitch. Then again the blade being longer than the tongue gives a greater range of angles without reduction from the full scale to obtain the side cuts of the jacks and hips, which with this system are always on the blade, thereby helping to more readily fix on the mind the different cuts and where they belong on the steel square.

What Constitutes a Full Pitch.—We find builders differ as to what constitutes a full pitch, and this is not to be wondered at, because writers on the subject differ. There are a number of books on the market, one of which has reached considerable sale, a copy of which is now before us, illustrating the pitch lines on the square similar to that shown in Fig. 196, but designating each line as a who'e, as 1, 2, 3, etc., pitch up to twenty-fourth pitch. Yet the universal theory of 12 and 12 taken on the square gives the seat and plumb cuts for the one-half pitch is the accepted practice and must prevail. What is true in this

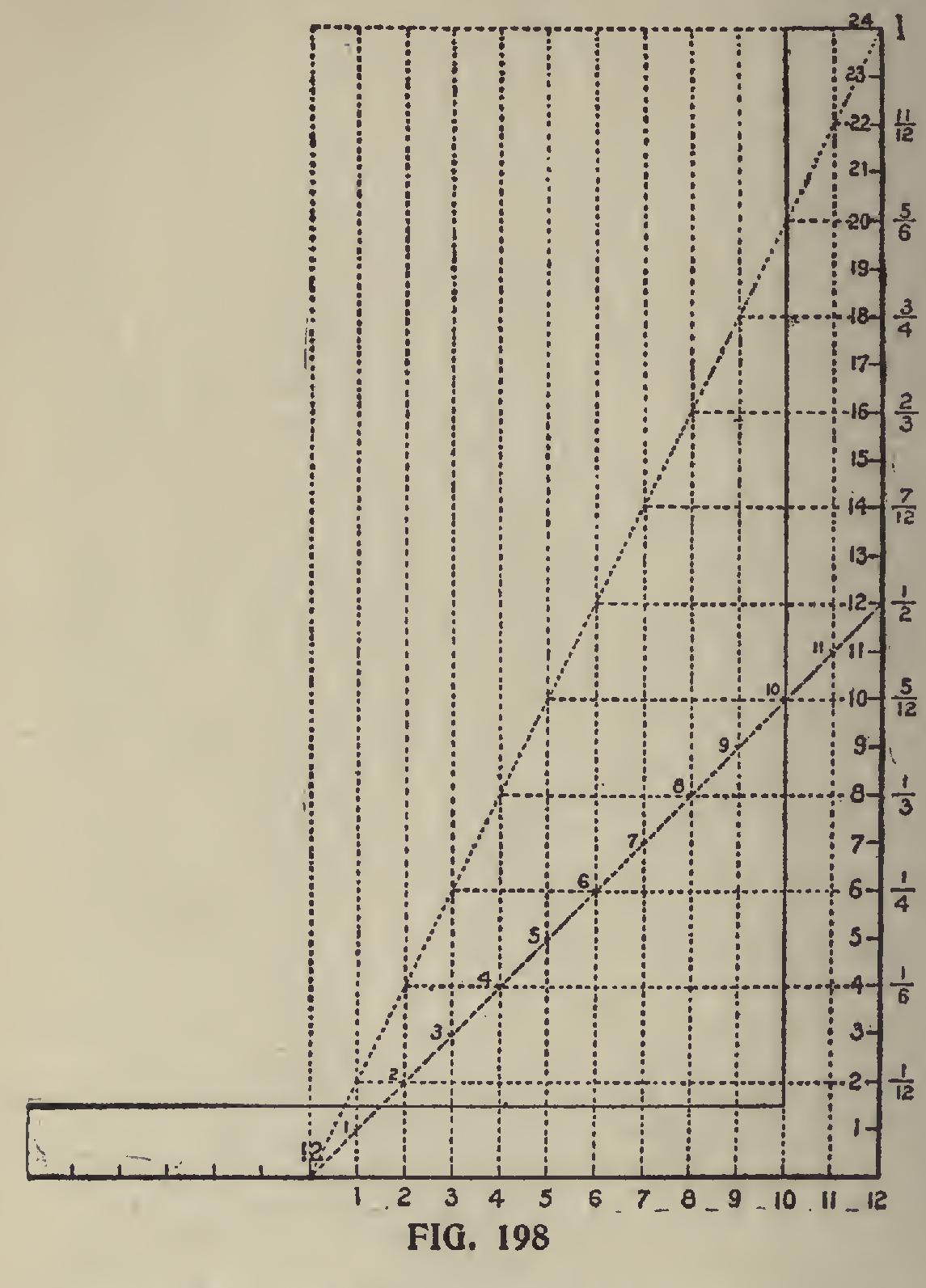
case must naturally follow when other figures are taken on the blade. Comparing it with the above method, twelve whole things would only be one half of a thing. Six whole things are one-fourth of a thing, etc. In saying this we do not mean to be understood that we are trying to introduce some new fangled theory about pitches; far from it. We take it as is usual in the accepted practice and analyze it. In other words, if there is such a thing as one-quarter, one-third, one-half, three quarter pitch, etc., then there must be a full pitch. This is arrived at by reckoning the rise given the common rafter in proportion to the span or width of the gable. It is therefore a full or a whole pitch when the rise equals the span. Taking it on the square ;—the run being 12 inches, the span must necessarily be 24 inches and since the blade is 24 inches long, then the figures on that member are to the pitch as to its own (blade) length, and that is all there is to it. Then a line drawn from 12 on the tongue to each of the inch divisions on the blade will represent as many fractional pitches. These lines diverge from one another taken on the vertical line at the rate of one-twelfth of an inch to each inch in run. So at the twelfth-inch back from the starting point, the lines are 12-12 or one inch apart and intersects the blade at the inch divisions and represents the full scale for a one-foot run for all GS the pitch lines. Now let us look at the figures on the blade of the square, as shown in Fig. 198, and see what relation they bear to those on the tongue. These figures as before explained represent the rise given the common rafter to a one-foot run. The fractional numbers to the right of the blade represent the proportion of the pitch. Now fol low the horizontal dotted lines from these figures over to the full or one pitch, thence down to the desired pitch and the figures at this point and those in the run taken on the square will be to the same proportion as those for the full scale, but at different points on the square. For illustration see the one-half pitch.