Pitches and Roof Framing

In Fig. 199 is shown a similar drawing, but in this the squares are reduced in size ranging from one-twelfth up to the full size square. The fractional figures that denote the pitch, also denote the size of the squares in proportion to the full size square and these, if divided into as many parts as the full size square would give just the same results as far as the cuts and bevels are concerned, as will be seen by taking the one-half pitch, the line passes at the half-way point on the blade of all of the squares and consequently would give like results. However, squares are not made other than with the standard measurements. This illustration is given simply to illustrate propor tional scales and that the size of the square would make no difference in the results so long as the divisions are to the ratio of the standard scale of measurements.

But we are not through talking about Fig. 198. In this illustration the vertical dotted lines from each inch in run represent the blade and the figures where the one-half pitch line crosses these lines and that denoting the run will give the seat and plumb cuts for the common rafter, as 1 and 1, 2 and 2, 3 and 3, etc. Now let us apply this to some other pitch. For an example we will take three-eighths pitch, as shown in Fig. 200. Remember the full pitch regulates the scale in proportion to the full scale for any rise under 24 inches. The full scale for the i pitch is 12 and 9. Why? Because 9 is i of 24.

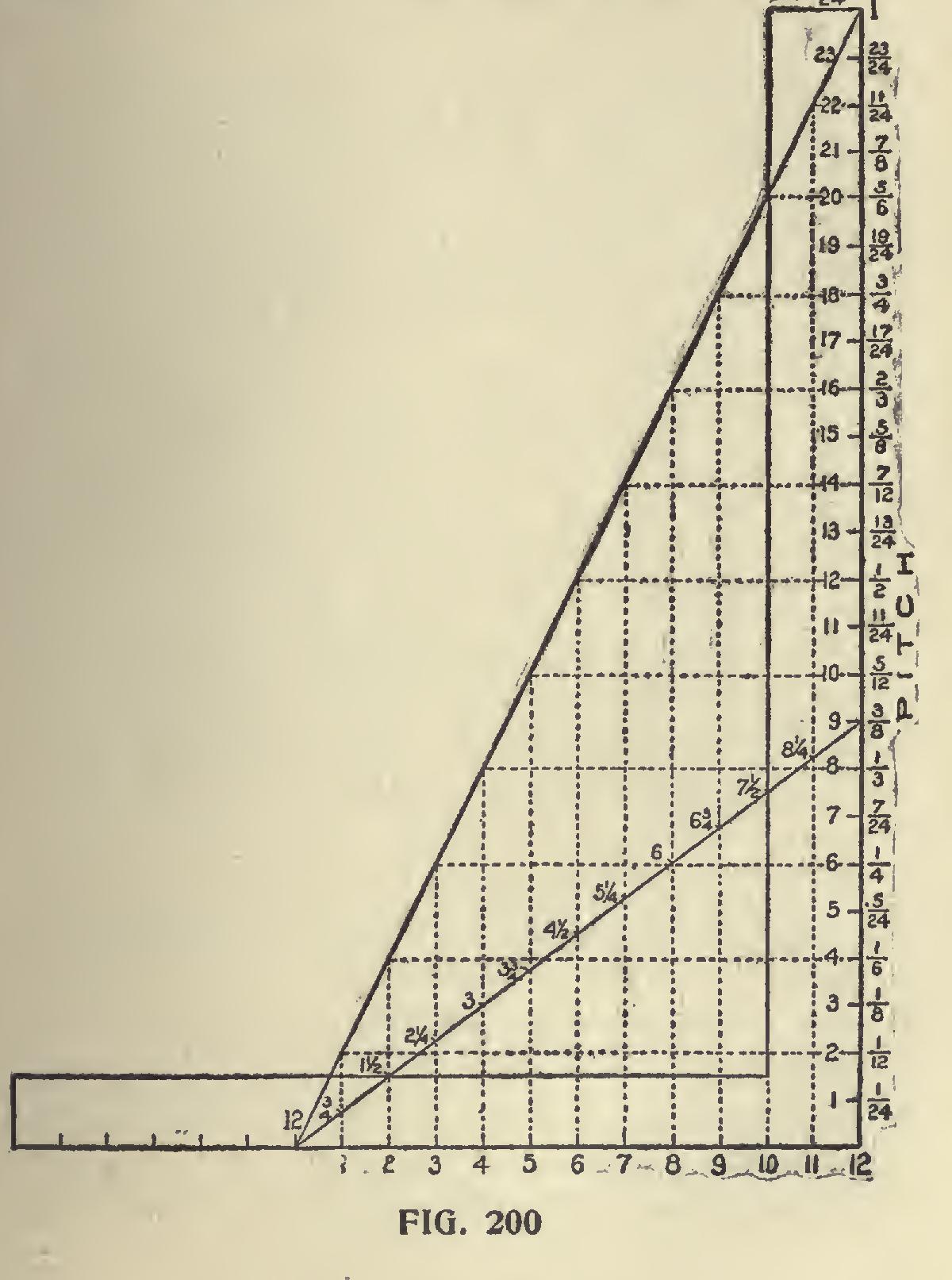
To find the I scale for the above pitch, take 6 on the blade and follow the horizontal line to the left till it intersects the one pitch, thence vertically down to the I pitch, and it will be found that this intersection is at 21 inches above 3 on the run, and it will be seen that these figures are i that of 9 and 12.

For the 5-12 scale, proceed in like manner, starting from 10 on the blade. The intersection on the pitch line will be 3i inches above 5 on the run. Thus every inch of the blade's length rep resents a distinct scale, and these are subject to many more scales. If the blade of the square be divided in twelfth inches, each division will rep resent a scale, making in all 12 multiplied by 24, equals 288 different scales; but these divisions run into intricate fractions for the rise, and only one half of the runs will end in twelfths of an inch. The other half will end in twenty-fourths, but all of these scales will be in the same ratio as that given for the full scale, and consequently give the same result as far as the angles are concerned.

However, it is better to use the full scale when same can be done, as it is handier and insures more accuracy in the work.

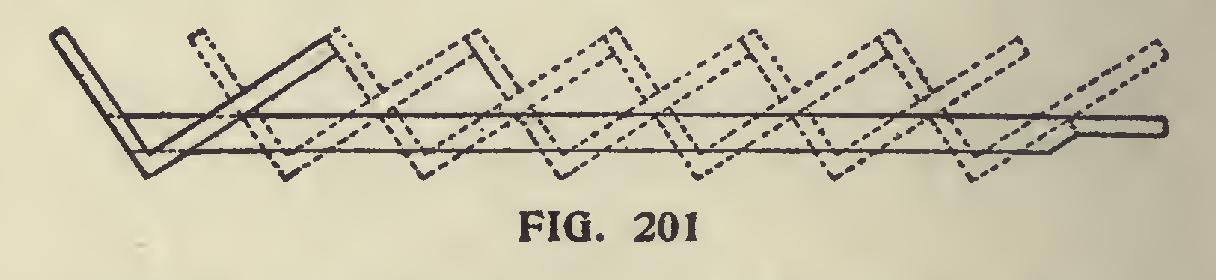
To Cut Rafters with The Square.

Fig. 201 il lustrates a way to cut rafters with a square. A roof 14 feet wide would have a run of 7 feet, third-pitch would rise 8 inches to every foot run. Therefore, place the square on 8 and 12 seven times, and you have the length and cuts.

Fig. 202. For the octagon rafter, proceed same as for common rafter, only use 13 for run (in place of 12 for common rafter).

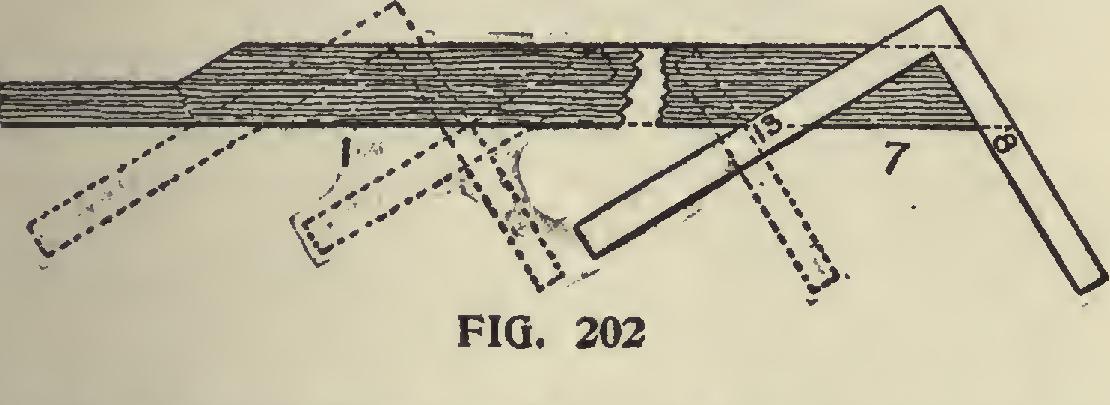
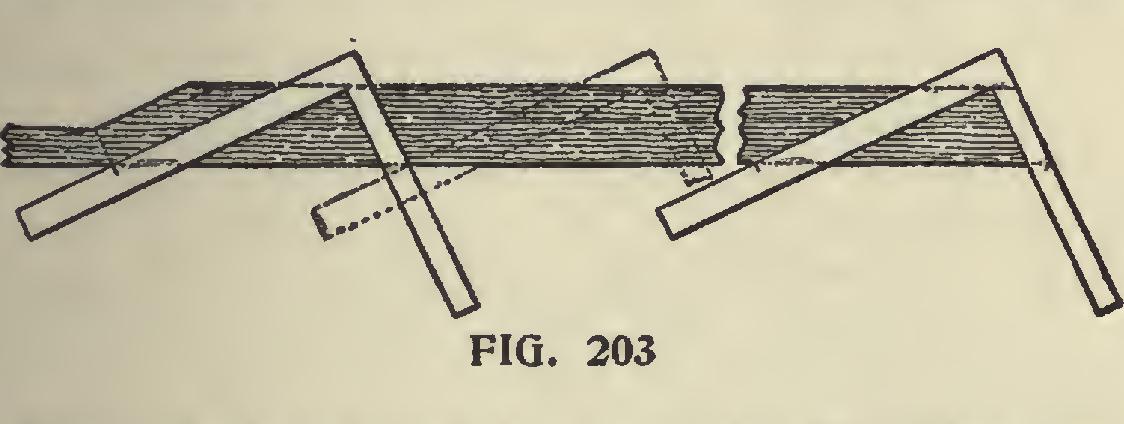
Fig. 203, hip or valley rafter. As these rafters run diagonal with the common rafter and as the diagonal of one foot is practically 17 inches, use 17 for run, and proceed the same as for common rafter.

Length of

there are to be five, divide the common rafter into six equal parts, use that for a pattern, and it gives the length very nicely. But that will not always work. To get all the dif ferent lengths might at first, look difficult even to many good mechanics, but it is very simple as illustrated in Fig. 204. If the first jack was one foot from corner, apply the square the same as for common rafter, and it gives length and cut (mark the length for starting point on next), and if it is 17 inches from the other, move the square up to 17, if the next is 15 move up to 15 and so on.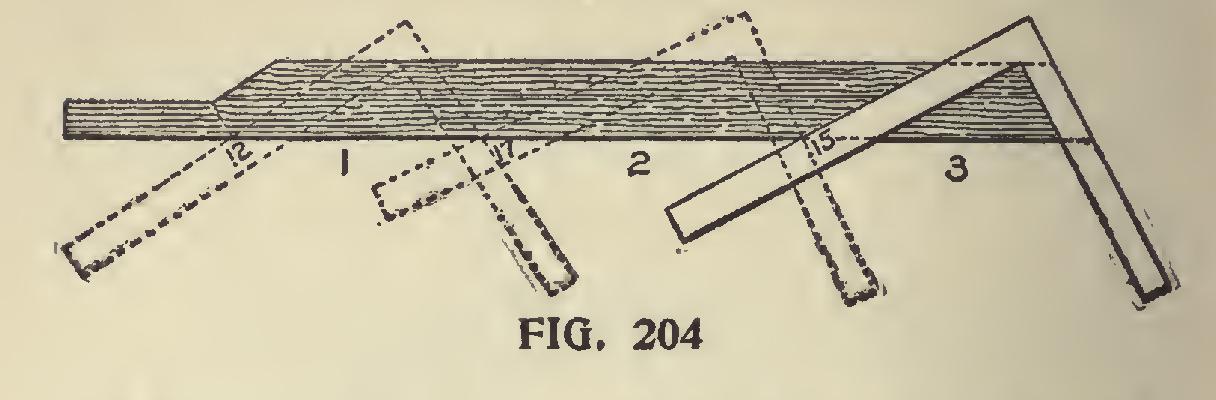

Fig. 205. The side cut of jack to fit hip, if laid down level would, of course, be square miter, but the more the hip rises the sharper the angle. Measure across the square from 8 to 12, and it is nearly 14i, which is the length of rafter to one foot of run. Length and run, cut on length, gives the cut.

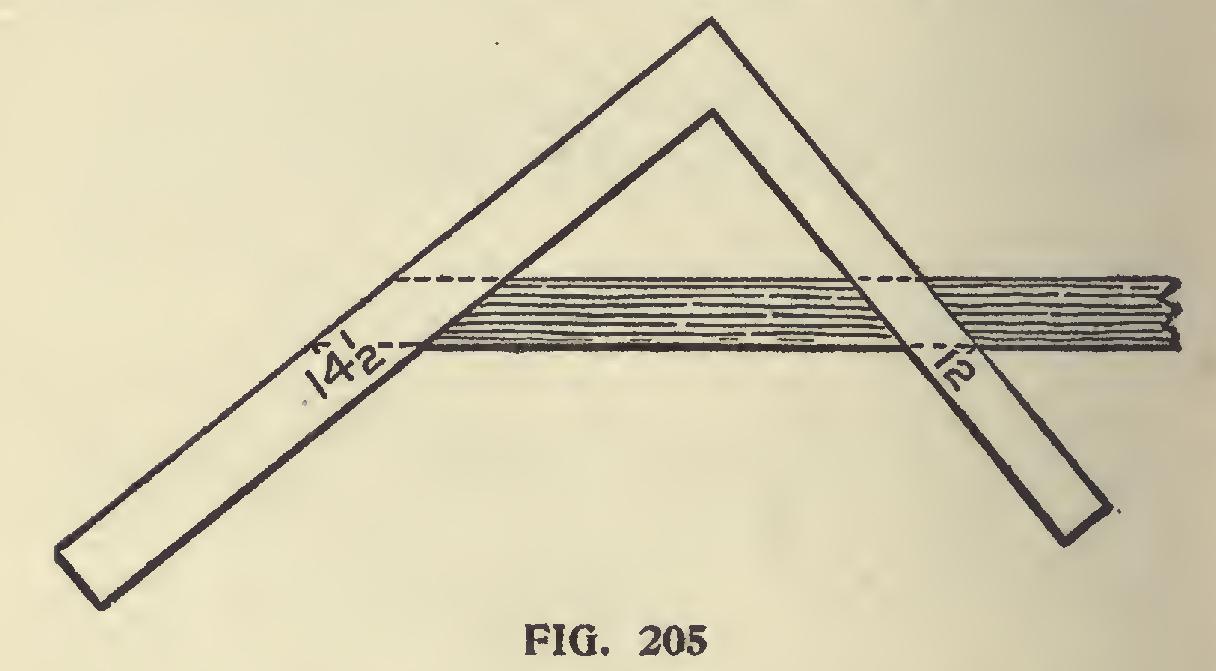
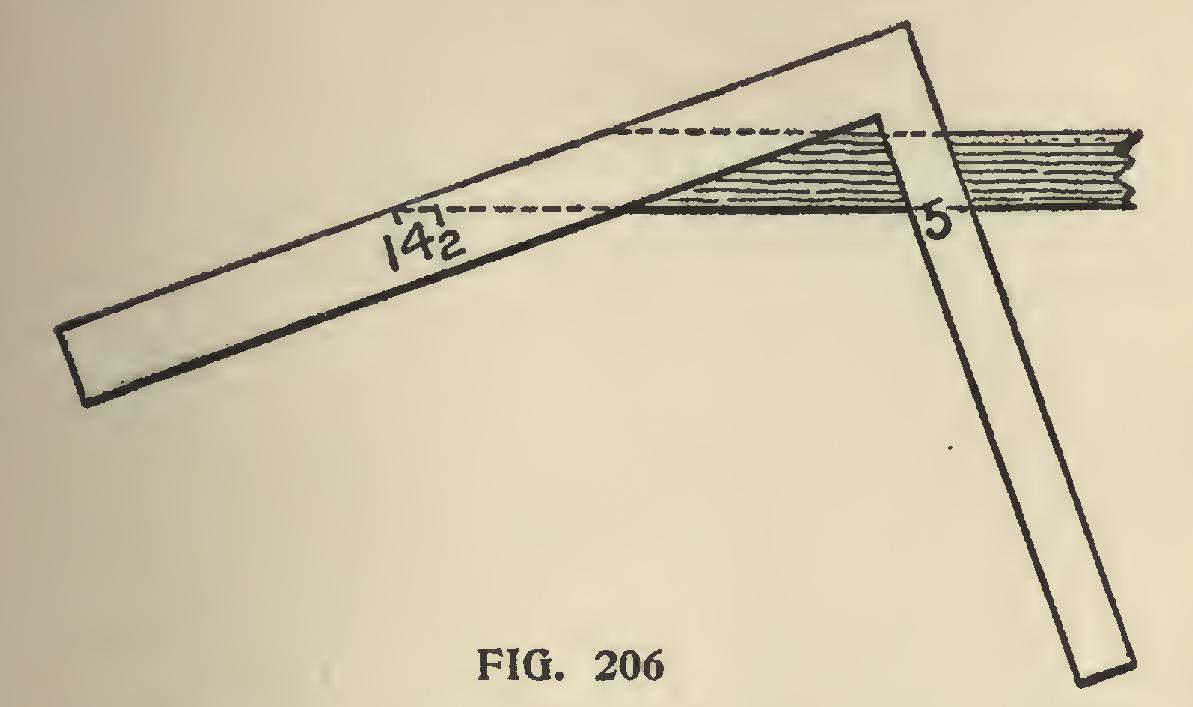
Fig. 206, octagon jack. As the octagon timer on level surface is 5 and 12, it must raise same as common jack, and is, therefore, raised to length, or 14i, and 5 cut on length.

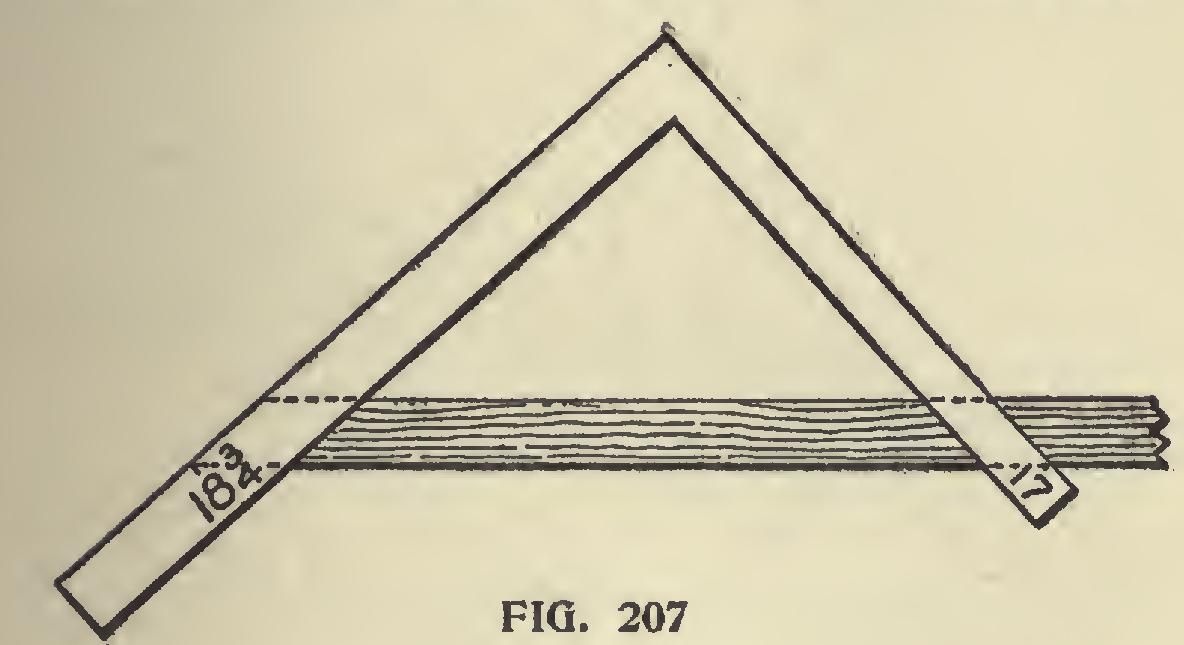
Fig. 207, hip rafter, is also length and run, cut on length.

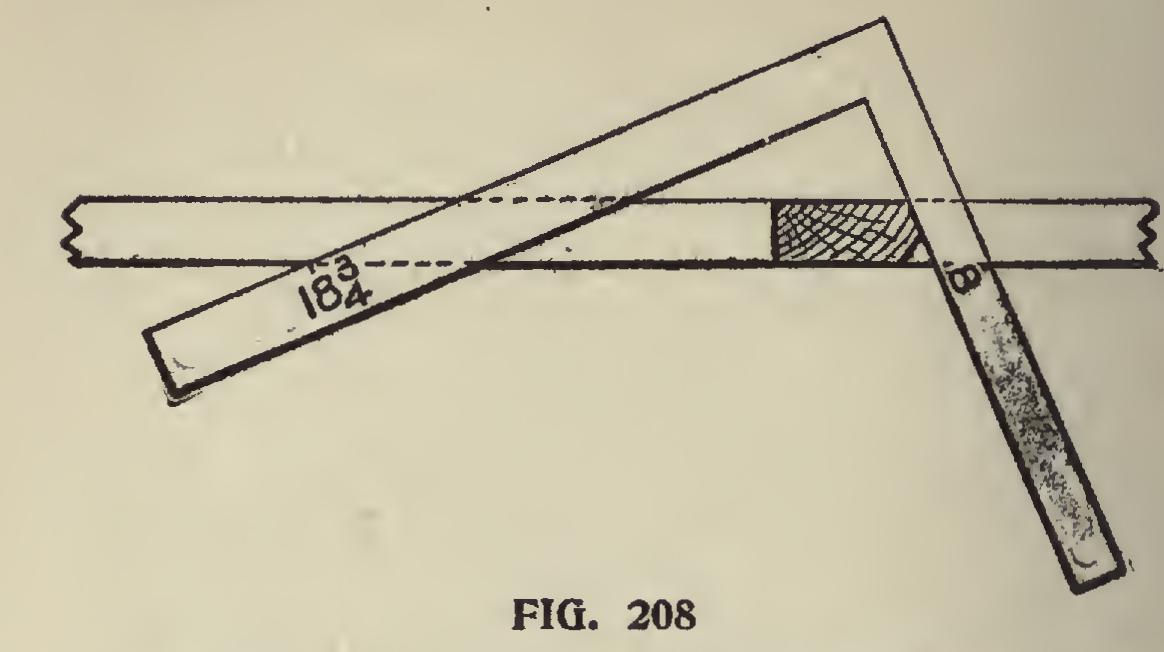
Fig. 208. To bevel top of hip take rise and mark on rise.

Fig. 209 is another practical way, which is simply to lay the square on heel of hip. The illus tration explains itself.

Simplest Way to Frame a Roof.—Perhaps the most practical way of all to frame a roof, the sim plest to understand, easiest to remember, and most rapid to apply, is simply to always take the rise and run, measure across the square which gives the length. Rise and run gives cuts, so you have it all.