Pitches and Roof Framing

For example we will take the pitch. Take 9 on the blade. Why? Because, the run being 12 inches, the span must be two times 12, which equals 24, and since the pitch is reckoned by the span, we find that of 24 is 9, and therefore rep resents the rise to the foot run. Then 12 and 9 gives the seat and plumb cut of the common rafter. They also give the cuts for the gable boards resting either horizontally or perpendicularly as shown in Fig. 218.

The Cuts, Lengths and Bevels of Rafters

are all contained in the cube as shown in Fig. 219. The base of the cube being twelve inches square, while the altitude is regulated by the rise given the com mon rafter to a one-foot run, which in this case is 9 inches or pitch. This is one of the best meth ods of fixing on the mind the true position of the different rafters and why certain figures are used on the square to obtain the cuts. We will carry this thought a little further and show the corner of a hip roof in an imaginary cube with dimensions equal the run and rise given the common rafter, as shown in Fig. 220. Here the common rafter, the jacks and the hip are shown in position with their relative runs, rises, lengths, cuts and bevels all shown in this illustration. If the corners of the building are other than at right angles, then the base of the cube would be to the same shape as that of the corner of the building.

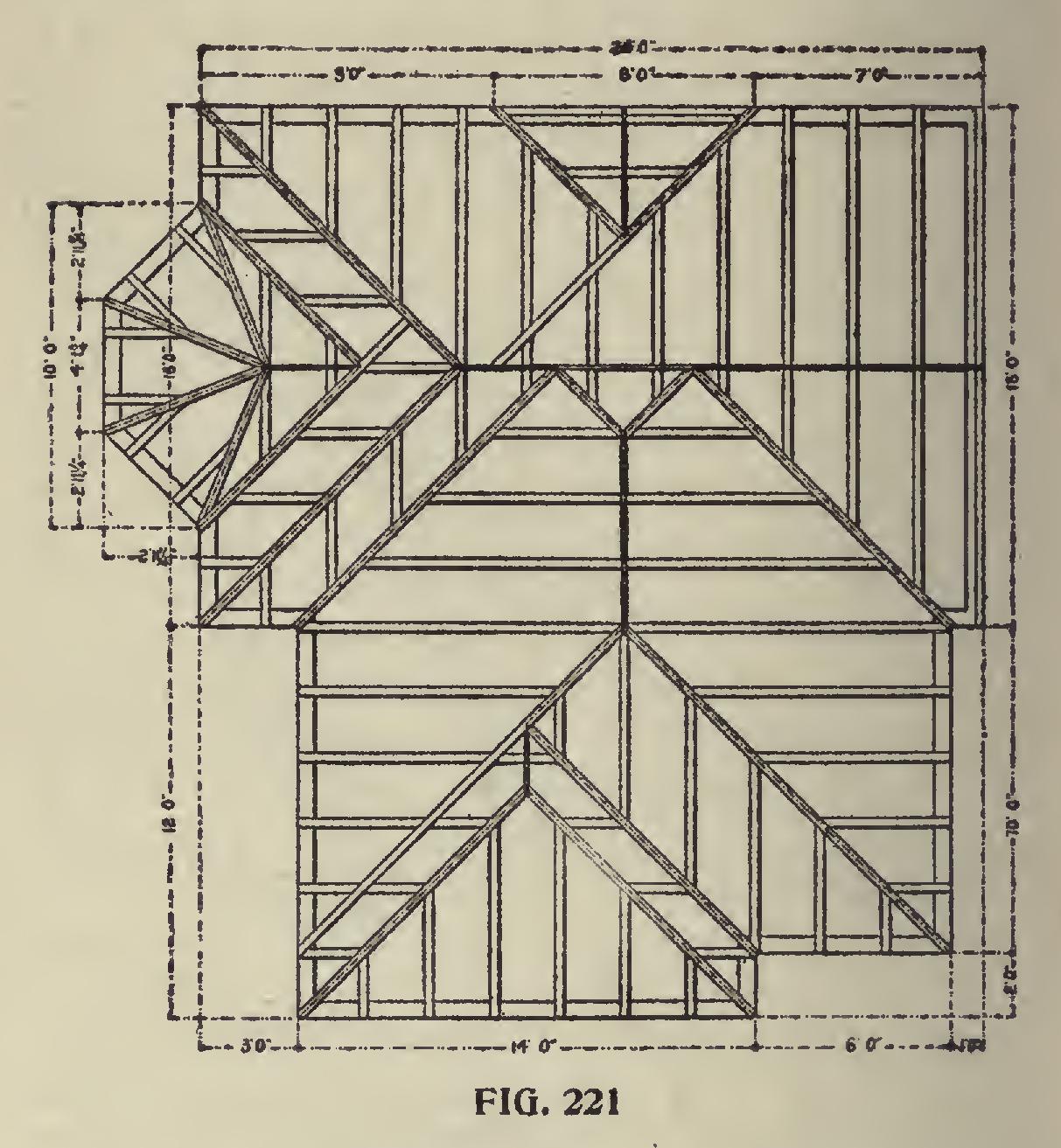
Plan of Roof.—In Fig. 221 is shown a roof plan with right-angled corners and containing an octagon bay. This answers for any pitch given the roof, as there is nothing in it to distinguish the pitch.

In fact it would show just the same if there was no pitch given at all, consequently all of the angles for the side cuts are at an angle of 45 degrees. If there was no pitch, it would simply be the common miter of 12 and 12 on the steel square, 12 being used on one arm of the square because it represents the length of the tangent when the run is one foot and remains so regardless of the pitch given the roof. 12 is used on the other arm of the square because it represents the length of the rafter for one-foot run when there is no pitch given. Therefore, we let 12 on the tongue represent the tangent because it is a fixed number and answers for any pitch. 'When there is a pitch given the rafter, its length is increased. Thus, in the pitch, the length is 15 inches. Therefore, 12 on the tongue and 15 on the

blade gives the side cut of the jack as before il lustrated. If we were to cut off the peak end of the jack rafter on a parallel line with the seat cut after the side cut. has been made, the angle would show just what we started from—the 45-degree angle. For the side cut of the hip, it would be 12 and 6 6-17, but in order to avoid the fractions it is better to use 17 on the tongue, as described in connection with the above figure.

The run and tangent in the case of the square cornered building being equal is very mis leading. 12 taken on one arm of the square is generally ascribed to the run, when, as a matter of fact, it has nothing to do with it. The run of the, rafter and its length (which gives the same result as 12 on the tongue and the length of the rafter for a one-foot run taken on the blade) gives the side cut of the jack rafter for the square-cor nered building and no other. Not because 12 stands for one-foot run of the common rafter, as is generally supposed, but because the tangent equals the run, and is therefore not a general rule, but one of the things that centralizes at 45 degrees.

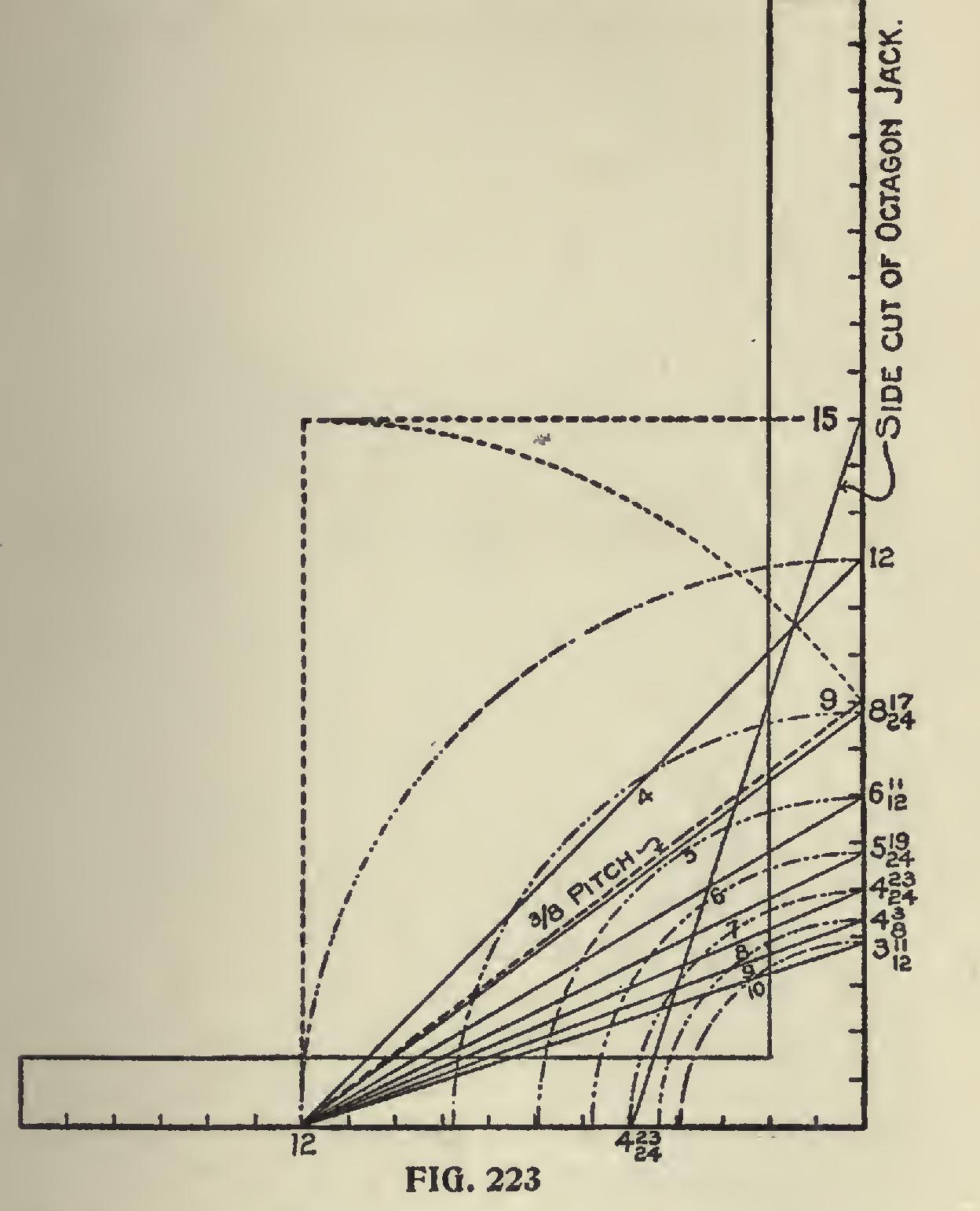
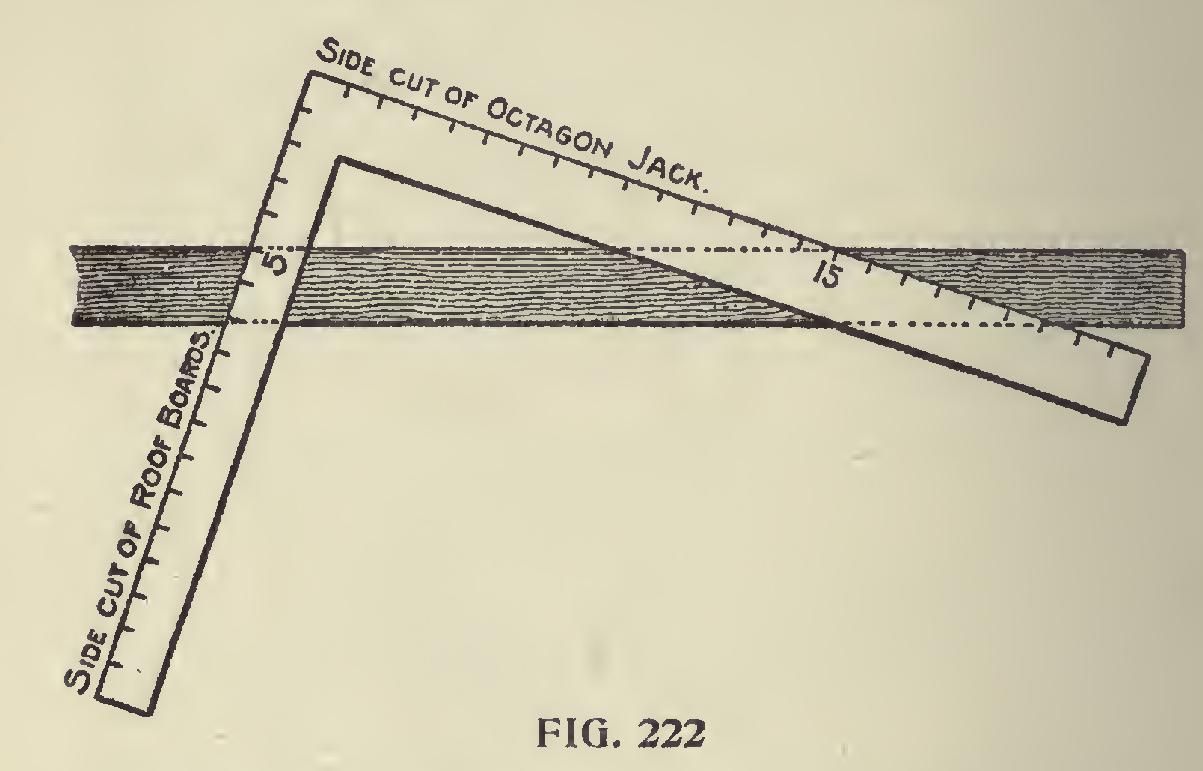
Now let us apply our unity rule, which, as will be seen, applies to any kind of a corner, whether square or any other shape. The rule applies to all alike. It is the tangent or the figures on the blade that give the miter when 12 is used on the tongue. These figures transferred to the tongue, and the length of the common rafter for a one-foot run of the given pitch taken on the blade will give the cut. The blade giving the cut. Now, for an octagon roof. The tangent for the octagon is 4 23-24 or practically 5 inches. This taken on the tongue and 15 (the length of the rafter for the pitch) on the blade gives the side cut of the jack, and the corresponding cut across the face of the roof board to fit over the hip. The blade giving the cut in the former and the tongue in the latter, as shown in Fig. 222.

What is true of this, is true of any other poly gonal roof. In Fig. 223 we show the tangents on the blade for the polygons from 4 to 10 and rep resent the figures to use on the tongue of the steel square instead of 12, as in the square-cornered building. In connection with this illustration are shown the figures to use for the octagon as applied in Fig. 222.